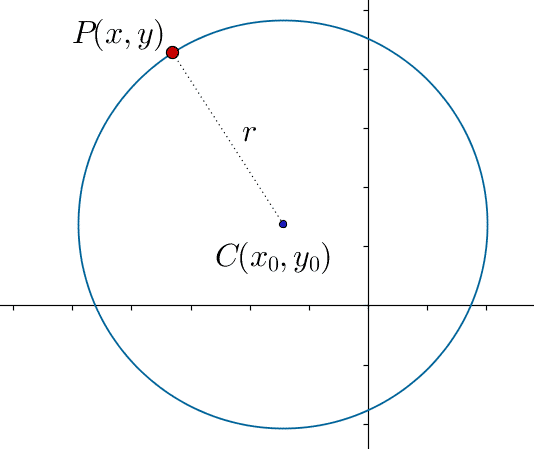
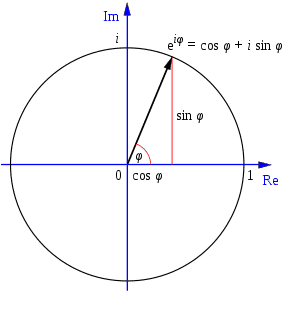
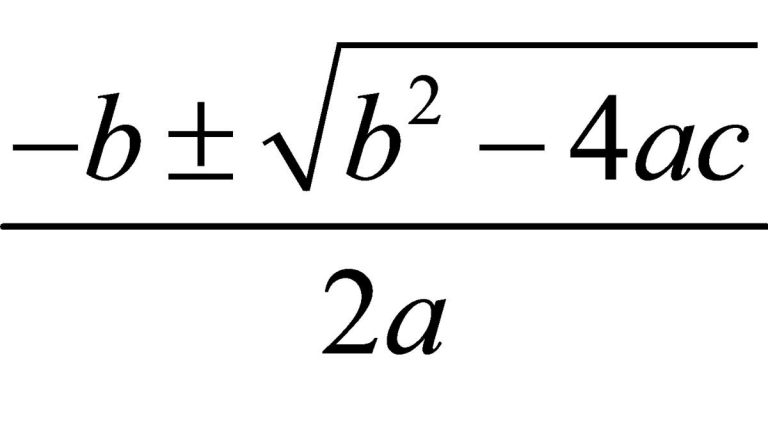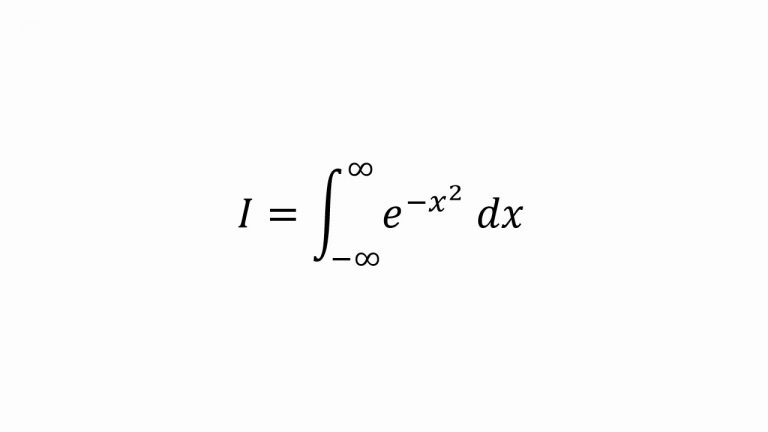Demostración geométrica y algebraica del teorema de Pitágoras
El teorema de Pitágoras, las fórmulas básicas de área y volumen y la mítica ecuación para resolver ecuaciones de segundo grado es lo único que la mayoría de la gente que no ha estudiado una carrera técnica recuerda de las matemáticas de instituto. El teorema de Pitágoras es uno de los teoremas más antiguos que …