
¡Buenas! En esta entrada vamos a ver el juego de la cuerda y el conejo, un acertijo matemático bastante curioso y para nada intuitivo.
Enunciado
Supongamos que el planeta Tierra es esférico y tiene un radio de 6371km (6.371.000 metros).
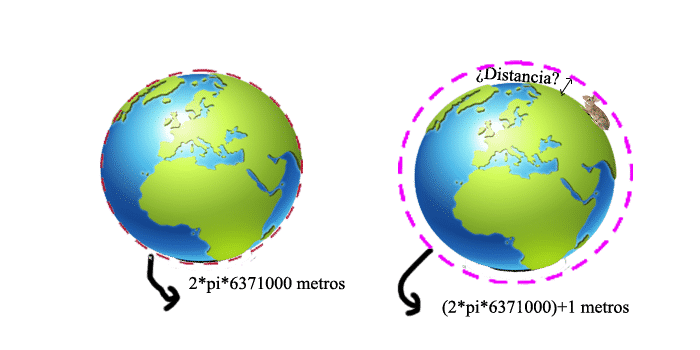
Supongamos que tenemos una cuerda muy muy larga y rodeamos el planeta con ella por el ecuador de forma que quede completamente pegada a la superficie de la tierra. Hablamos de una cuerda que mide \(2\pi *6371000\) metros
Si tomamos una cuerda que mida 1 metro más que la anterior, es decir, \((2\pi *6371000)+1\) metros y la colocamos alrededor de la tierra… ¿Tendrá suficiente holgura para que pase un conejo por debajo de la cuerda? Suponemos que un conejo mide de alto estando tumbado unos 15-16cm.
Toma la imagen como referencia para comprender el enunciado y haz las cuentas si te atreves. Encontrarás la solución justo debajo.
La solución
Vamos a hacer las cuentas.
Tenemos un radio de 6371000 metros y la cuerda tiene una longitud de \(2\pi *6371000\) metros. Si queremos calcular la holgura que presenta respecto al radio terrestre debemos de dividir dicha longitud entre 2pi y restarle el radio terrestre, pero obviamente obtenemos 0 metros de holgura.
En el caso de la cuerda alargada, tenemos una cuerda de \((2\pi *6371000)+1\) metros. ¿Cuál es la holgura que presenta?
- Radio terrestre: \(R\)
- Radio cuerda: \(\frac{2\pi R +1}{2\pi}=R+\frac{1}{2\pi}\)
Diferencia de radios: \((R+\frac{1}{2\pi})-(R)= \frac{1}{2\pi}=0,159…\) metros
Lo que supone una holgura de 15,9 centímetros aproximadamente, la justa para que quepa un conejo.
Explicación
Sorprendente, ¿Verdad? Pero, ¿Por qué ocurre esto? Empleando letras en lugar de valores numéricos se ve claro.
Llamemos r al radio genérico de cualquier esfera (Planeta tierra, pelota de fútbol, pelota de tenis, canica…) y d a la holgura o diferencia de radios inicial y final. r’ será el radio final tras alargar la cuerda.
Se tiene que la longitud inicial es 2*pi*r, y la final es 2*pi*r+l (l es la longitud extra que alargamos). Si calculamos el radio final tras alargar una longitud l obtenemos un radio \(r’=r+\frac{l}{2\pi}\)
Por lo que la holgura es \(d=\frac{l}{2\pi}\) que es constante, de manera que alargando 1 metro la cuerda que rodea a cualquier esfera obtendremos una holgura de 15,9cm siempre.
Esto se debe a que existe una relación lineal entre la longitud de una cuerda y su radio. De hecho, la propia definición del número pi garantiza que el cociente entre la longitud de la cuerda y el diámetro es constante y vale exactamente pi.
Por tanto, si se suma una cantidad a la longitud se obtiene un aumento proporcional del radio. \(f(x+a)=\gamma a+ f(x)\)



Muy curioso la intuición dice lo contrario
Mi intuición dice que 1 m/2pi se ve muy pegado comparado al diámetro de la tierra.
Lo que no entiendo dónde está la paradoja.
Claro, la intuición dice que, si tú tienes una cuerda de millones de metros que va pegada a la tierra, si la cuerda es 1 metro más larga, prácticamente no va a afectar a nada puesto que la cuerda es prácticamente la misma. No obstante, tendríamos una cuerda que se podría separar una gran distancia del suelo, tanta como para que pasen varios conejos sin problemas
No es exactamente una paradoja es más un hecho que choca contra la intuición. Yo lo llamaría más bien “acertijo”.
“Una paradoja es una idea lógicamente contradictoria u opuesta a lo que se considera verdadero a la opinión general. También se considera paradoja a una proposición en apariencia falsa o que infringe el sentido común”
Ostras, llámalo como quieras pero sigue siendo una paradoja.
si
Buen artículo!
jaja que bueno
Esta bueno
Y que hay del desplazamiento del objeto para que toda la holgura quede del sitio por donde tiene que pasar el conejo. Es decir, con la cuerda corta la tierra evidentemente está en el centro pero con un metro más se puede desplazar a un lado. Y eso provocaría el aumento del espacio
Buenos días “Anónimo” gracias por su comentario
Este es un estudio teórico que tiene como finalidad demostrar la relación lineal entre la longitud de una circunferencia y su radio
Supongo que entiendo lo que dice. ¿Qué sucede su además de alargar la cuerda en vez de levantarla x centímetros en todos los puntos de la tierra a la vez, la pegásemos y levantaramos toda la holgura en un punto?
Es una pregunta interesante pero la respuesta es un poco incierta. Y se debe a que no está definida la forma en la que hacemos la holgura (Forma parábola, circunferencia, catenaria?)
El exceso de cuerda se conoce, y es 1 metro. Si hacemos la holgura a partir del trozo de cuerda sobrante haciendo una circunferencia, la circunferencia tendría un diámetro de 1/pi = 2*r = 2*15,9 ~ 32 centímetros.
Sería el doble de la holgura que obtendríamos si la levantásemos en todos los puntos como indica el estudio.
Un saludo!