La parábola. Desarrollo de su ecuación y propiedad focal. Cónicas III

En esta tercera entrada acerca de las cónicas vamos a hablar de otra cónica bastante simple y conocida: la parábola.

Se denomina cónica o sección cónica a la curva resultante de la intersección entre un cono y un plano. Existen cuatro cónicas: circunferencias, elipses, parábolas e hipérbolas.

Una parábola se produce cuando un cono se ve cortado por un plano inclinado que llega a cortar la base también pero sin una inclinación tan elevada que se genera una hipérbola:

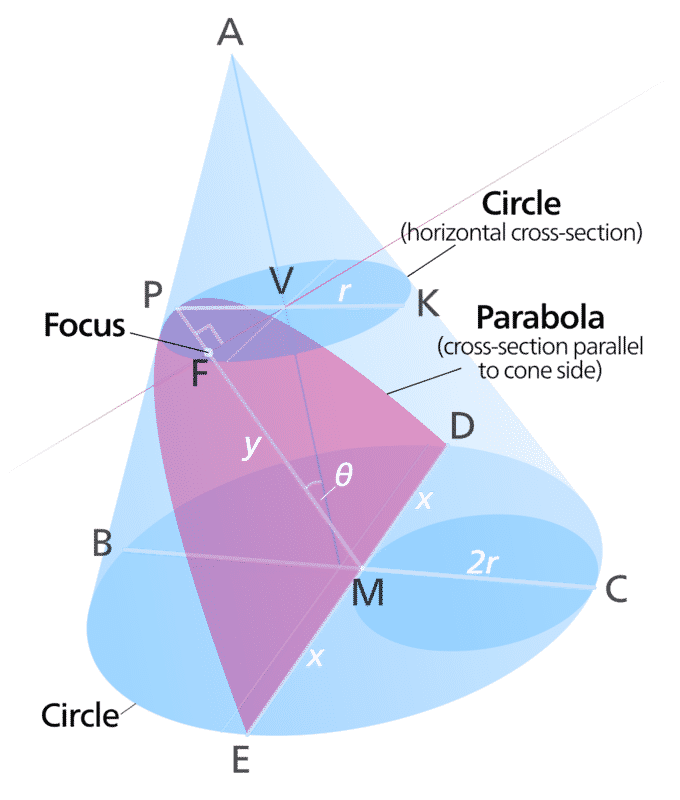
Demostración algebraica de la ecuación de la parábola

Se denomina parábola al lugar geométrico de los puntos del plano que equidistan (perpendicularmente) de una recta fija, llamada directriz, y de un punto fijo en el plano, que no pertenece ni a la parábola ni a la directriz, llamado foco.

A continuación se presenta un esquemático de los puntos que cumplen dicha condición (parábola en sí) junto con la definición de la directriz, vértice y el foco.

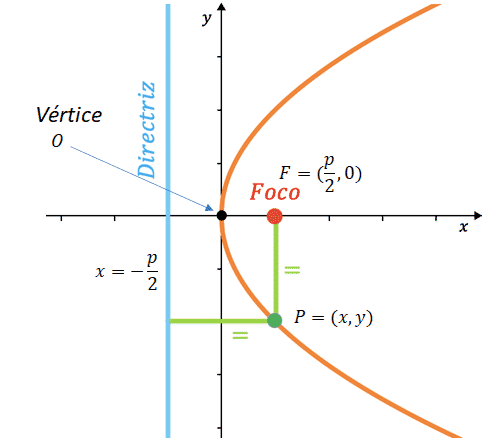
Se denomina \(p\) al parámetro de la parábola. Dicho parámetro se define como la distancia entre el foco y la directriz, y además es el único parámetro que define la forma de la parábola una vez se ha situado en el sistema de referencia. El comportamiento es el siguiente:

• Si aumenta el parámetro, la parábola toma una forma más abierta. El caso absurdo sería con \(p\) infinito, donde la directriz se encuentra a una distancia infinita, y por lo tanto los puntos que cumplen con la definición de la parábola estarían en el infinito, o lo que es lo mismo, contenidos en una recta vertical pasando por el origen de coordenadas.
• Si disminuye el parámetro, la parábola toma una forma más cerrada. El caso absurdo sería con \(p=0\), donde el foco se encuentra en la directriz y por lo tanto los únicos puntos que cumplen con la definición de la parábola serían los contenidos en una recta perpendicular a la directriz pasando por el origen ya que habría la misma distancia al foco que perpendicularmente a la directriz.

Ecuación

Si denominamos P al punto genérico de la parábola, F al foco (situado según la imagen en el (p/2,0)), y D a la directriz (situada en la recta x=-p/2), la ecuación o restricción que debe verificarse es:

\( d(P,D) = d(P,F)\)

Se recuerda que la distancia entre dos puntos en un plano se obtiene de la siguiente manera:

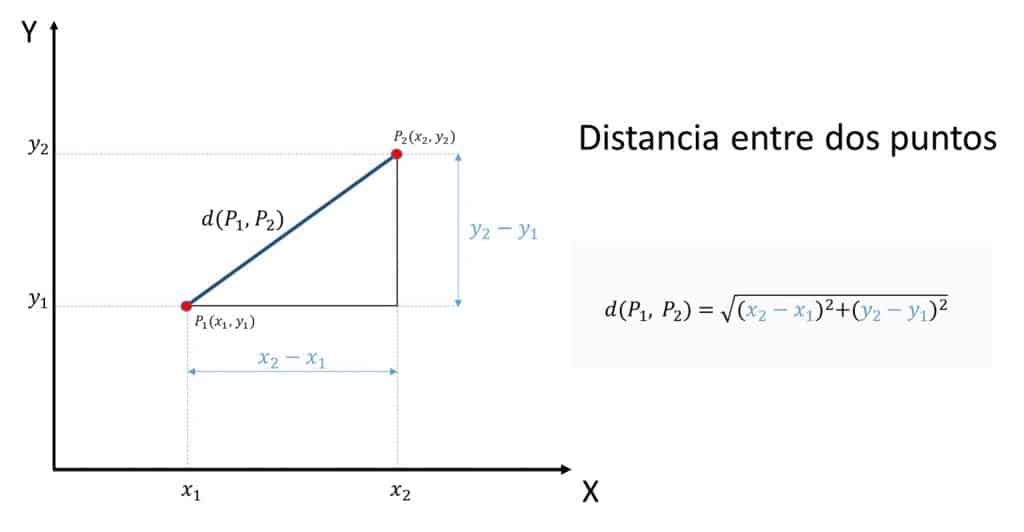
Por lo tanto las distancias son:

\(d(P,D) = |x+ \dfrac{p}{2}|\)

\(d(P,F) = \sqrt{(x-\dfrac{p}{2})^{2} + y^{2}}\)

Igualando dichas distancias:

\(|x+ \dfrac{p}{2}| = \sqrt{(x-\dfrac{p}{2})^{2} + y^{2}}\)

Elevando al cuadrado eliminamos la raíz y nos podemos despreocupar del valor absoluto:

\(x^{2} + \dfrac{p^{2}}{4} + px = x^{2} + \dfrac{p^{2}}{4} – px + y^{2}\)

Eliminando términos y reagrupando llegamos a la ecuación final:

\(y^{2} = 2px\)

Obsérvese que \(y\) aparece al cuadrado para poder representar ambas ramas de la parábola. De lo contrario, si aplicamos la raíz cuadrada estaremos representando sólo la rama superior. Si cambiamos la posición de \(x\) e \(y\), tendríamos una parábola vertical.

\(x^{2} = 2py\)

Si despejamos la \(y\), podemos representar la parábola al completo:

\(y=\dfrac{x^{2}}{2p}\)

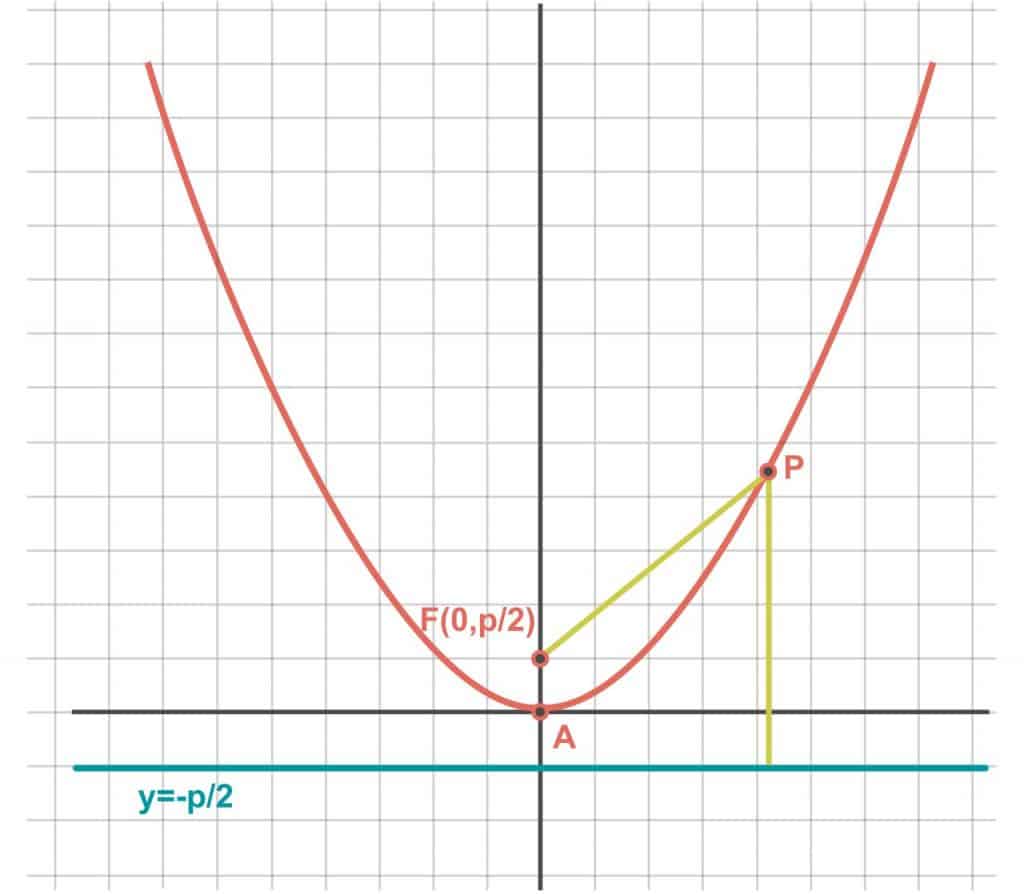
Análogamente como se hizo con la elipse, puede obtenerse la ecuación en el caso de que el vértice no se encuentre situado en el (0,0) sino en un punto genérico \((x_{0},y_{0})\). Las coordenadas del resto de puntos y directriz serían:

Punto genérico de la curva parabólica (\(x,y\))

Punto del foco (\(x_{0}+\dfrac{p}{2},y_{0}\))

Directriz (\(x=x_{0}-\dfrac{p}{2}\))

Sin embargo no es necesario hacer el desarrollo de nuevo. Si hacemos un cambio de variable (o de notación más bien) considerando el punto genérico como:

• \(x’=x-x_{0}\)
• \(y’=y-y_{0}\)

Se tiene que al restar las coordenadas para calcular la distancia entre los puntos se llega a la misma ecuación en términos de las nuevas variables:

\(|x’+ \dfrac{p}{2}| = \sqrt{(x’-\dfrac{p}{2})^{2} + y’^{2}}\)

Desarrollando de la misma forma se llega a la misma ecuación:

\(y’^{2} = 2px’\)

Deshaciendo el cambio de variables:

\((y-y_{0})^{2} = 2p(x-x_{0})\)

Propiedad focal de la parábola

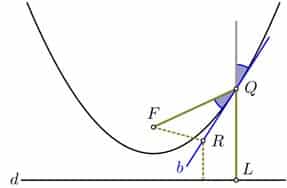
En cada punto de la parábola, la recta tangente forma un ángulo tal que su normal es la bisectriz entre el ángulo formado por las rectas que unen el foco y el punto con una recta perpendicular a la directriz.

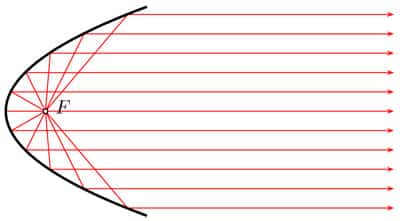
Es decir, dicha propiedad, en términos físicos, implica que cualquier rayo que proceda paralelo al eje de la parábola al rebotar va a ir siempre hacia el foco. Y viceversa, cualquier rayo que parta del foco se ve reflejado paralelo al eje de la parábola.

Si una parábola se hace girar alrededor de su eje de simetría se forma una superficie conocida como paraboloide elíptico, que se presenta a continuación.

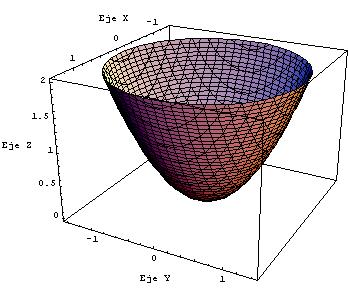
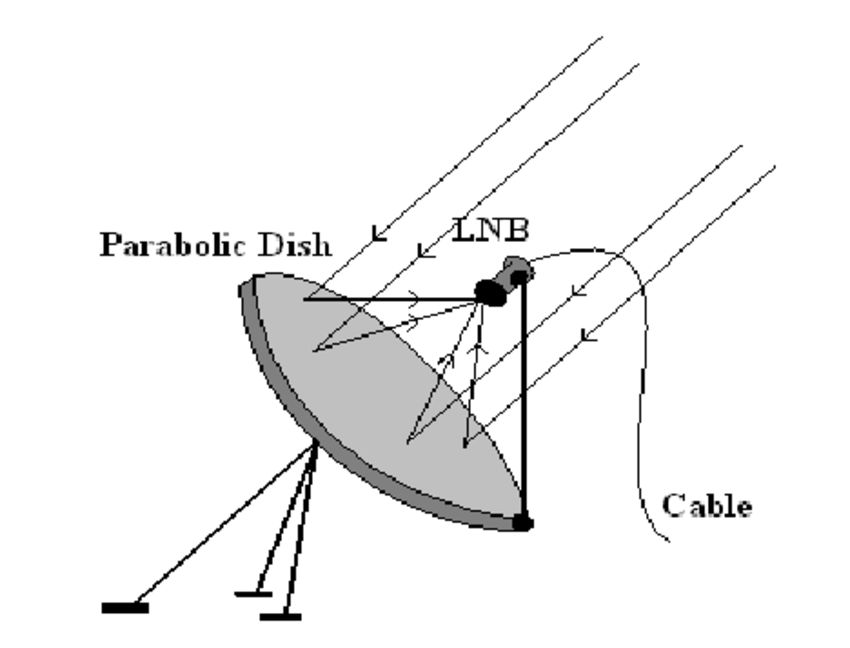
Dicha superficie tiene la misma propiedad pero tridimensionalmente, es decir, que cualquier rayo que venga paralelo al eje de revolución al rebotar irá al foco. Esta es una propiedad muy interesante que se le da como uso más conocido en las antenas parabólicas.

Los satélites de televisión se encuentran en una órbita geoestacionaria, es decir, una órbita tal que el satélite siempre se encuentra sobre un punto fijo de la superficie terrestre (porque el satélite se mueve a una velocidad que coincide con la de rotación de la Tierra).

Esto se hace así para poder apuntar desde la Tierra al satélite y así poder recibir la señal de televisión. Sin embargo, sería muy complicado apuntar con tanta precisión al satélite. Por ello se usa una antena parabólica, es decir, una antena o receptor de ondas electromagnéticas que se sitúa en el foco de un paraboloide. De esta manera, con orientar la antena en una dirección aproximada la cantidad de radiación que se recibe es tan alta que se obtiene una señal muy limpia.

Además, hay que tener en cuenta que al estar el satélite tan alejado, la radiación, si bien no se emite perfectamente orientada hacia la Tierra, a una distancia tan grande la radiación llega casi paralela a una recta que une el satélite con el centro de la Tierra. De hecho, si la distancia al satélite es de 35.786.000 metros y supongamos que una antena parabólica tiene un radio proyectado de 0.5 metros, el ángulo que forman 2 rayos recibidos en los extremos del paraboloide es de 8e-7º, es decir, el ángulo del sector circular de un pelo visto desde 6 kilómetros. En resumen, que puede considerarse que los rayos vienen paralelos como ocurre con la radiación solar por ejemplo.

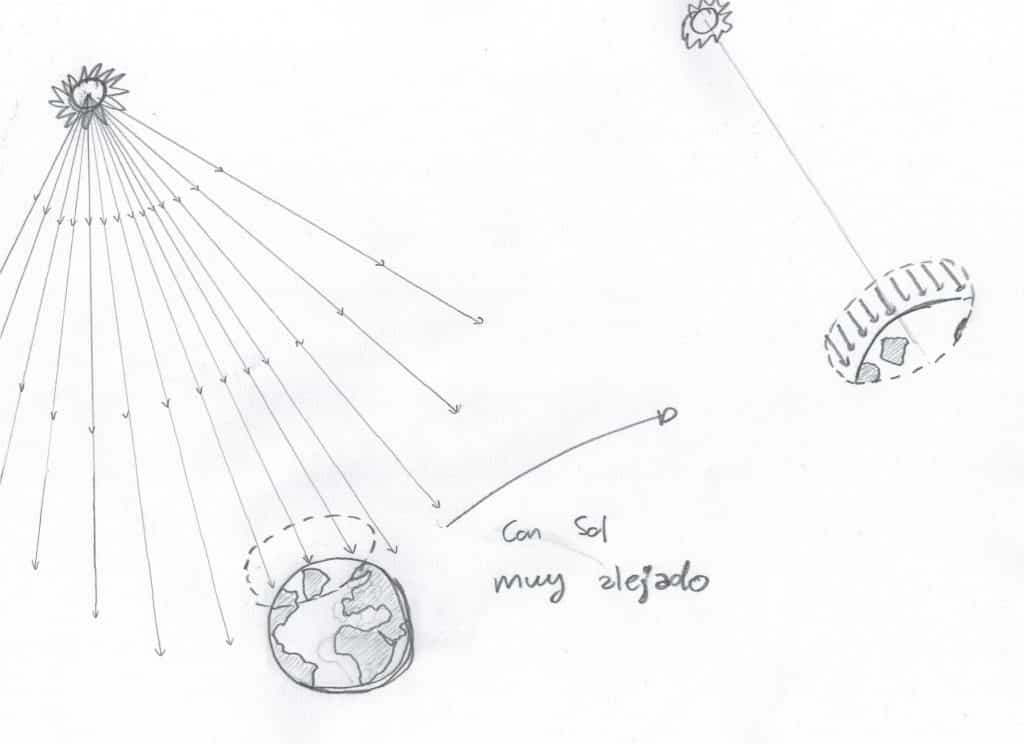
De esta manera, no es necesario calibrar la antena para cada una de las casas. Con poner la antena apuntando hacia una dirección aproximada, el paraboloide se encarga de concentrar la información.

Se usan también los paraboloides en las linternas y en los focos de los coches. De esta manera, no se ilumina todo el ambiente como ocurre con una bombilla, sino que sólo se ilumina lo que nosotros queremos iluminar, permitiendo además mayor potencia lumínica al concentrar los rayos al frente.

Si os interesan las propiedades reflectivas y cómo se han ido empleando las distintas geometrías como la elipse para dicho fin, en este interesante artículo encontrarás bastante información acerca de los reflectores.