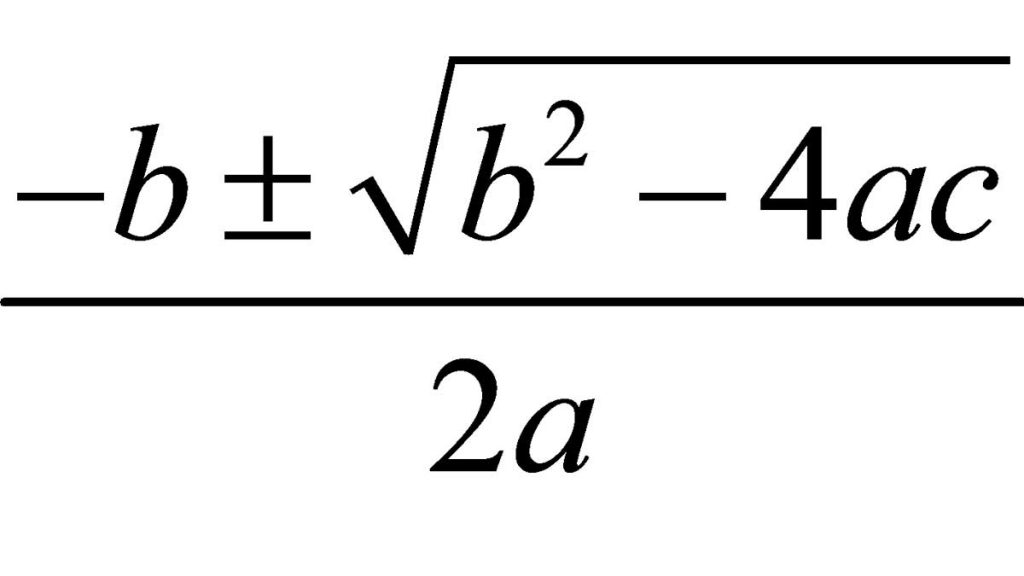
Introducción
Estoy seguro de que cualquiera que esté leyendo este artículo reconoce esta fórmula a pesar de no cursar estudios relacionados con las matemáticas.
Es la fórmula que todos hemos aprendido en el instituto y tenemos grabado a fuego cada vez que queremos hallar la raíz de un polinomio de segundo grado de la forma \(ax^{2}+bx+c=0\)
Pero, ¿Sabéis de dónde procede la fórmula para hallar las soluciones de las ecuaciones de segundo grado? Vamos a hacer un poco de álgebra para que lo puedan entender tanto los curiosos de las matemáticas como aquellos que tienen cierta discalculia (Dificultades para comprender las matemáticas)
El binomio al cuadrado
Antes de deducir dicha fórmula debemos de emplear otra más básica y conocida por todos: la fórmula del binomio al cuadrado.
Se tiene que: \((a+b)^{2}=a^{2}+b^{2}+2ab\)
Completando el binomio al cuadrado
Sabiendo la relación de izquierda a derecha podemos hacer lo mismo pero al revés; teniendo varios términos al cuadrado y cruzados agruparlos en una suma o resta elevada al cuadrado. Y esto es precisamente lo que debemos hacer para sacar la fórmula que estamos buscando.
\(4a^{2}+b^{2}+4ab+5c=(2a+b)^{2}+5c\)Deducción de la fórmula
Agrupando términos
Para empezar quitamos el coeficiente al monomio de mayor grado:
\(ax^{2}+bx+c=0->x^{2}+\frac{b}{a}x+\frac{c}{a}=0\)Observamos 3 términos de los cuales uno de ellos está al cuadrado y el otro parece ser un término cruzado. ¿Os suena de algo? Efectivamente, podemos agruparlos en forma de binomio.
Identificando términos
- Uno de los sumandos claramente es x
- El término cruzado es \( \frac{b}{a}x \) por lo que deducimos que el otro sumando es \( \frac{b}{2a} \)
Ya tenemos los sumandos de nuestro binomio al cuadrado de forma que podemos agrupar varios términos y principalmente quitar ese cuadrado a la x
Vamos a ver qué obtenemos agrupando términos tal y como hemos dicho:
\((x+ \frac{b}{2a})^{2}=x^{2}+ \frac{b^{2}}{4a^{2}}+ \frac{b}{a}x \)Observamos que:
- Nos sobra \( \frac{b^{2}}{4a^{2}} \)
- Nos falta \( \frac{c}{a} \)
Por ello para hallar la equivalencia entre ambas formas sólo tenemos que sumar y restar términos.
\(x^{2}+\frac{b}{a}x+\frac{c}{a}=0->( x+ \frac{b}{2a})^{2}- \frac{b^{2}}{4a^{2}} + \frac{c}{a} = ( x+ \frac{b}{2a})^{2} – \frac{b^{2}-4ac}{4a^{2}} =0\)Agrupando términos y dejando el binomio a un lado nos queda:
\( ( x+ \frac{b}{2a})^{2} = \frac{b^{2}-4ac}{4a^{2}} \)Haciendo la raíz cuadrada:
\(x+ \frac{b}{2a} =\pm \sqrt{\frac{b^{2}-4ac}{4a^{2}}}=\pm \frac{\sqrt{ b^{2}-4ac }}{2a}\)Finalmente, pasando el término a la derecha y dejando x solo nos queda:
\(x = -\frac{b}{2a} \pm \frac{\sqrt{ b^{2}-4ac }}{2a} =\frac{-b \pm \sqrt{b^{2}-4ac}}{2a}\)Resultando ser la fórmula tan conocida y empleada para hallar las soluciones de ecuaciones de segundo grado.
Haciendo la raíz cuadrada
Una vez completado el binomio basta con hacer la raíz cuadrada a ambos términos y obtendremos una x sin ningún exponente. Sin embargo, debemos de recordar que estamos en álgebra y no podemos tomarnos a la ligera esta operación.
Estamos buscando los valores de x que cumplen esa relación. Observamos que puede haber (Y de hecho hay) 2 valores de x que cumplen dicha relación ya que lo que hay dentro del paréntesis puede tomar un valor positivo y negativo que al cuadrado sea idéntico al término de la derecha.
Llegados a este paso \( ( x+ \frac{b}{2a})^{2} = \frac{b^{2}-4ac}{4a^{2}} \) sacamos la siguientes conclusiones:
- Si el término de la derecha no es nulo y b no es nulo x toma valores diferentes
- Si el término de la derecha es nulo tenemos un valor doble de x
- Si b es nulo tenemos dos soluciones de x que son idénticas con el signo cambiado
- Si el término de la derecha es negativo tenemos 2 soluciones complejas
Estos 4 casos se representan gráficamente respectivamente:
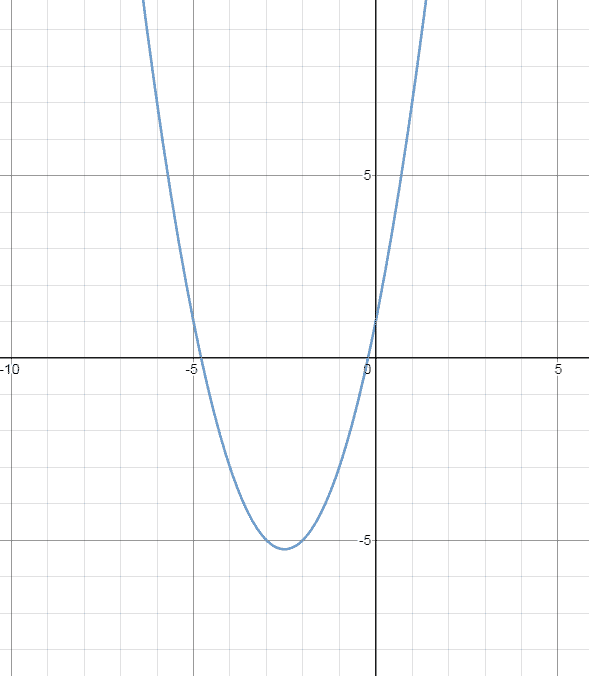
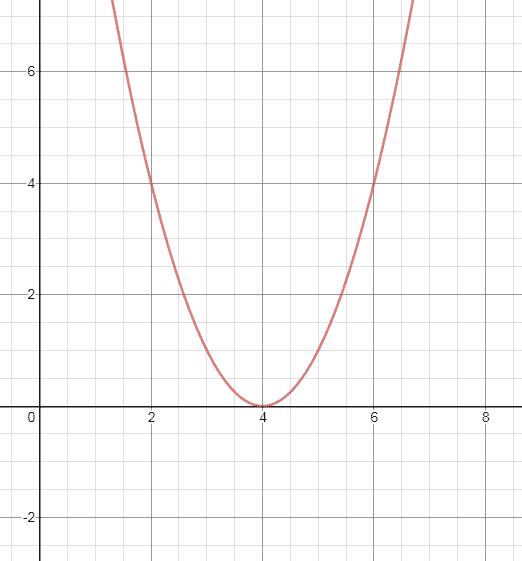
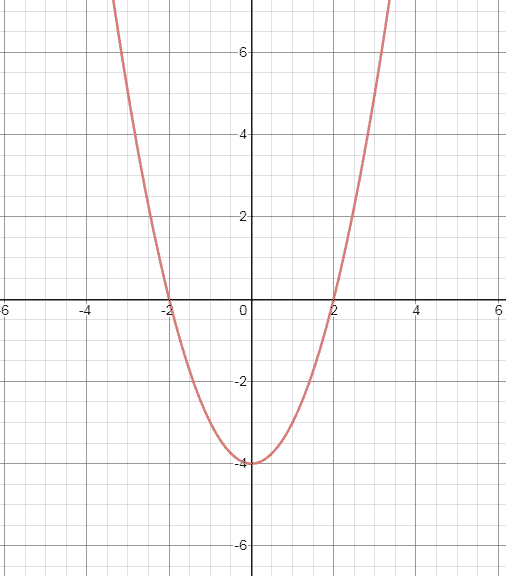
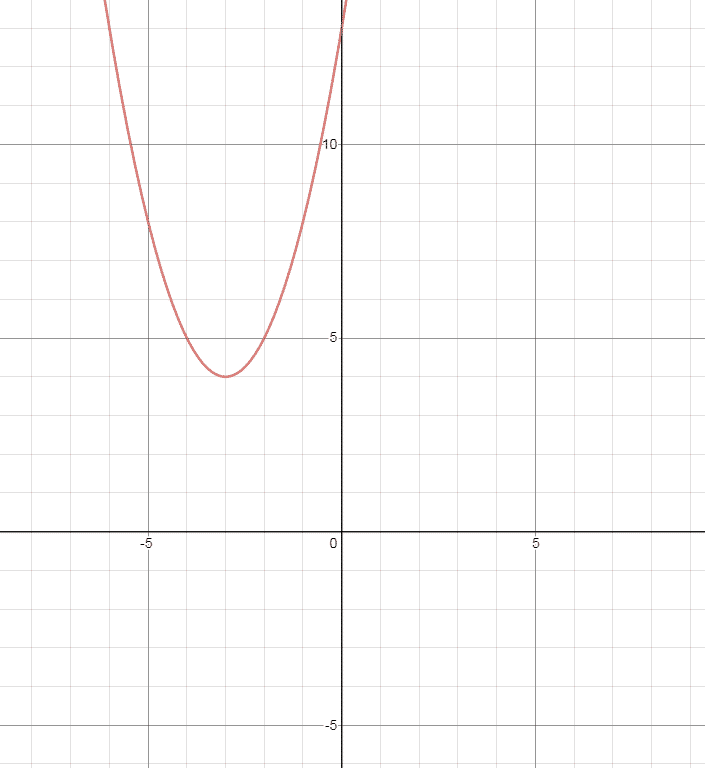
Gráficos generados con Desmos.com



4 comentarios en «La famosa fórmula de ecuaciones de segundo grado»