La fórmula de Euler

La fórmula

La fórmula de Euler o relación de Euler, atribuida a Leonhard Euler, establece el teorema, en el que:

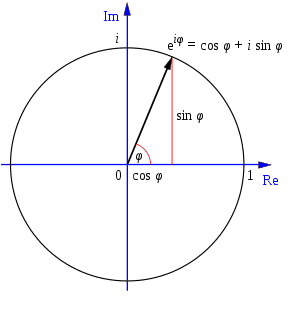
\(e^{ix}=\cos(x)+i\sin(x)\)

Para todo número real x. También se emplea la generalización:

\(e^{z}=e^{x+yi}=e^{x}*e^{yi}=e^{x}(\cos(y)+i\sin(y))\)

La fórmula puede interpretarse geométricamente como una circunferencia de radio unidad en el plano complejo, dibujada por la función \(e^{ix}\) al variar x sobre los números reales. Así, x es el ángulo de la recta que recorre la circunferencia unidad, medido en sentido contrario a las agujas del reloj y en radianes.

En el caso de z=x+yi, y representa el ángulo en radianes mientras que x representa el radio, pudiendo generalizar la circunferencia unidad a circunferencia de radio cualquiera.

Tiene una gran utilidad a la hora de querer simplificar expresiones o unir términos, cobrando relevante importancia en la resolución de ecuaciones diferenciales o en el análisis de señales.

La demostración

Para demostrar la equivalencia vamos a hacer un desarrollo en serie de las funciones \(e^{x}, \cos(x) \ y \ \sin(x)\). Igualaremos términos idénticos de las series, de forma que algebráicamente se demuestra la equivalencia entre las funciones. Desarrollando la serie de Maclaurin de dichas funciones se tiene que:

\( {\begin{aligned}e^{x}&{}={\frac {x^{0}}{0!}}+{\frac {x^{1}}{1!}}+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+{\frac {x^{4}}{4!}}+\cdots \\\cos x&{}={\frac {x^{0}}{0!}}-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots \\\sin x&{}={\frac {x^{1}}{1!}}-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots \end{aligned}} \)

(Al final de esta entrada se hizo un desarrollo en serie detallado para el número e)

Antes de comenzar a desarrollar las expresiones recordamos la unidad imaginaria i:

\( {\begin{aligned}i^{0}&{}=1,\quad &i^{1}&{}=i,\quad &i^{2}&{}=-1\quad &i^{3}&{}=-i,\\i^{4}&={}1,\quad &i^{5}&={}i,\quad &i^{6}&{}=-1,\quad &i^{7}&{}=-i,\\\end{aligned}} \)

---

Finalmente, si introducimos un número complejo zi, siendo z un número real e i la unidad imaginaria, se tiene:

\({\begin{aligned}e^{iz}&{}={\frac {(iz)^{0}}{0!}}+{\frac {(iz)^{1}}{1!}}+{\frac {(iz)^{2}}{2!}}+{\frac {(iz)^{3}}{3!}}+{\frac {(iz)^{4}}{4!}}+{\frac {(iz)^{5}}{5!}}+{\frac {(iz)^{6}}{6!}}+{\frac {(iz)^{7}}{7!}}+{\frac {(iz)^{8}}{8!}}+\cdots \\&{}={\frac {z^{0}}{0!}}+i{\frac {z^{1}}{1!}}-{\frac {z^{2}}{2!}}-i{\frac {z^{3}}{3!}}+{\frac {z^{4}}{4!}}+i{\frac {z^{5}}{5!}}-{\frac {z^{6}}{6!}}-i{\frac {z^{7}}{7!}}+{\frac {z^{8}}{8!}}+\cdots \\&{}=\left({\frac {z^{0}}{0!}}-{\frac {z^{2}}{2!}}+{\frac {z^{4}}{4!}}-{\frac {z^{6}}{6!}}+{\frac {z^{8}}{8!}}-\cdots \right)+i\left({\frac {z^{1}}{1!}}-{\frac {z^{3}}{3!}}+{\frac {z^{5}}{5!}}-{\frac {z^{7}}{7!}}+\cdots \right)\\&{}=\cos(z)+i\sin(z)\end{aligned}}\)

Expresión que coincide con la expuesta al inicio.

Caso particular: Identidad de Euler

Llegados a este punto, es muy sencillo comprender la identidad de Euler. Se da cuando el argumento es \(\pi\), es decir, \(x=\pi\)

\(e^{i\pi}=\cos(\pi)+i\sin(\pi)=-1 ——> e^{i\pi} +1=0 \)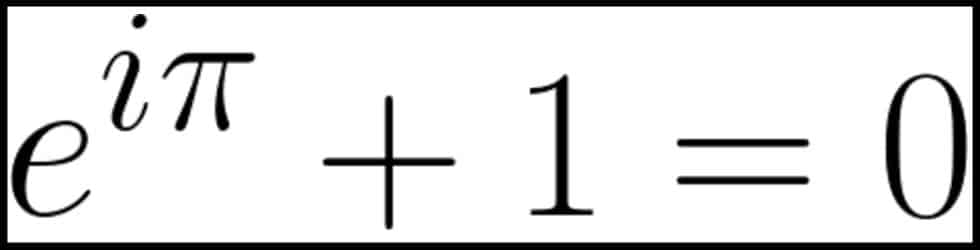

Logaritmo de números negativos

Hay que decir que, trabajando con números reales, no existen los logaritmos negativos. Esto se debe básicamente a la propia definición de un logaritmo, es decir, con \(log_{a}x=c\), se tiene que \(x=a^{c}\). Siendo a un número estrictamente mayor que 0 (De lo contrario el logaritmo no estaría bien definido), no existe ningún valor real de c tal que \(a^{c}\) sea < 0.

No obstante, en el terreno de los complejos, sí es posible. Además, empleando la fórmula de euler el cálculo se simplifica enormemente.

De la identidad de Euler sabemos que \(e^{\pi i}=-1\)

Y aplicando el logaritmo natural en ambos términos: \(ln(-1)=\pi i\), con lo cual definimos el valor del logaritmo negativo.

De esta forma, podemos calcular el valor de cualquier logaritmo negativo aplicando las propiedades de los logaritmos.

¿Qué valor tiene ln(-a)?

\(ln(-a)=ln(a)+ln(-1)=ln(a)+\pi i\)