Estoy seguro de que cualquiera que esté leyendo este artículo lo ha pensado en algún momento. Bien sea bebiendo un refresco, jugando a hundir el hielo en un vaso o tras ver en las noticias que sube el nivel del mar por derretirse los polos.
Y es que el agua es, a pesar de ser el líquido más común, el que posee las propiedades más extrañas. Y una de ellas es que, al disminuir su temperatura y pasar a fase sólida, aumenta su volumen. Esto implica que su densidad disminuya y que por tanto el hielo flote.
Vamos a demostrar matemáticamente si al derretirse un hielo que flota en agua hará que incremente el volumen de líquido o no.
Demostración de variación de volumen al derretirse el cubito
Supongamos un cubito de hielo en un vaso de agua con nivel de agua inicial Ho
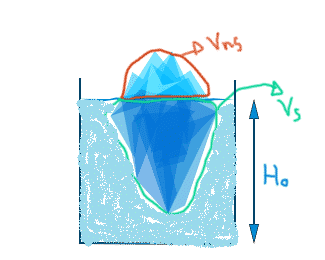
Llamemos \(V_{hielo} \) al volumen total del hielo, de forma que en todo momento \( V_{hielo} = V_{s}+V_{ns}\) haciendo referencia a “sumergido” y “no sumergido”.
Pero, ¿Qué relación existe entre las proporciones de Vs y Vns? Vamos a aplicar el Principio de Arquímedes en nuestra posición de equilibrio.
Recordemos en qué consiste este principio:
Un cuerpo total o parcialmente sumergido en un fluido en reposo experimenta un empuje vertical hacia arriba igual al peso del fluido desalojado
El peso total es \(P=\rho_{h} V_{hielo} g\)
El empuje recibido (Peso del líquido desplazado) es \(E=\rho_{a} V_{s} g\)
Siendo “h” de hielo y “a” de agua. Igualando E=P llegamos a:
\(V_{s}=\frac{\rho_{h}}{\rho_{a}}V_{hielo}\)
Lo que nos permite calcular cuanto volumen se sumerge en función de los datos (Densidades y volumen).
En esta situación de reposo con el hielo ocupando un volumen\(V_{s}\) se tiene que el nivel de agua es Ho. Vamos a calcular qué volumen total tendrá el cubito de hielo en forma líquida.
Primero aplicamos conservación de la masa. De esta forma se tiene que:
\(M_{hielo}=\rho_{h}V_{hielo}=\rho_{a} V_{derretido}\)
Siendo Vderretido el volumen de agua generado por el hielo al derretirse.
Despejando el valor de Vderretido:
\(V_{derretido}=\frac{ \rho_{h} }{ \rho_{a} } V_{hielo}\)Pero recordemos de la posición de equilibrio que la relación entre el volumen de hielo total y el sumergido es:
\(V_{hielo}=\frac{\rho_{a}}{\rho_{h}}V_{s}\)Introduciendo el término \(V_{hielo}\):
\(V_{derretido}=\frac{ \rho_{h} }{ \rho_{a} } * \frac{\rho_{a}}{\rho_{h}}V_{s} =V_{s}\)
Lo que demuestra que el volumen ocupado por la parte del hielo que se sumerge y el volumen total de agua que genera el hielo al derretirse es el mismo.
Por lo tanto, una vez derretido el nivel de agua no variará.
Si el nivel de agua no varía, ¿Por qué se habla del hielo de los polos y el nivel del agua?
Supongamos que tenemos un iceberg de varias toneladas flotando en medio del océano. Si este se derrite, aplicando el mismo planteamiento que con el cubito de hielo, el nivel de agua no variará. Sin embargo se asocia el deshielo con el incremento del nivel de los océanos.
Esto es porque, si bien una masa de hielo flotante no afecta al nivel del agua, el hielo que se derrite que se encuentra sobre tierra firme si. La Antártida por ejemplo es un continente cubierto completamente por hielo, pero este hielo no flota sobre el océano, sino que descansa sobre tierra firme. Por lo tanto, si se derrite el hielo y/o se desprende algún fragmento de hielo al océano, incrementará el nivel del agua (Así es como se forman los icebergs). Lo mismo ocurre con islas como Groenlandia o las del polo norte.
Otra conclusión del experimento
En este caso concreto nos hemos centrado en calcular cuanto volumen de hielo se sumerge dado las densidades, pero… ¿Por qué no hacer el caso inverso?
De nuestra fórmula:
\(V_{s}=\frac{\rho_{h}}{\rho_{a}}V_{hielo}\)Podemos extraer un valioso dato como es la densidad o incluso el peso de un cuerpo sin tener una balanza o cualquier instrumento mecánico. Sólo empleando líquidos y algún recipiente graduado… ¿Pero cómo?
Vamos a estudiar el caso general de tener un cubito de hielo de forma irregular y querer calcular su peso y su densidad sin tener una balanza. ¿Cómo lo hacemos?
Primero necesitamos conocer su volumen total. Para ello emplearemos el otro concepto que también introdujo Arquímedes y que popularizó la expresión ¡Eureka!; El volumen de un cuerpo sumergido en un líquido es igual al incremento de volumen del líquido.
Sin embargo, el hielo flota, y por ello no podemos conocer su volumen total. Llegados a este punto tendríamos dos opciones:
- Una sería tomar una piedra, meterla en nuestro vaso de medición con agua y medir su volumen. Luego, meter el cubito y poner encima la piedra, de manera que ambos cuerpos se sumerjan y calcular el volumen total. Ahora para calcular el volumen del hielo sólo tenemos que restar los volúmenes.
- Otra opción sería sumergir el hielo en un líquido con menor densidad. El aceite de oliva no nos vale puesto que su densidad es prácticamente idéntica a la del hielo, y no podemos asegurar que se hunda. Sin embargo, el alcohol (Etanol) es mucho menos denso (0,789 kg/L frente a los 0,916 kg/L del hielo). Un experimento curioso para saber si el cubata va demasiado cargado sería ver si los hielos se hunden [Quizás haga un artículo sobre ello :P]

Una vez conocido el volumen total del hielo, necesitamos conocer el volumen que se sumerge. Para ello sólo tendríamos que colocarlo en el vaso de medición con agua y ver cuanta agua se desplaza.
Una vez conocido estos datos y la densidad del agua (Que podemos suponer igual a 1) llegamos a:
\( \rho_{h} = \rho_{a} \frac{V_{s}}{ V_{hielo} }\approx \frac{V_{s}}{ V_{hielo} } \)
El peso de nuestro cubito de hielo no sería más que
\( M_{h} = \rho_{h} V_{h} \)
Si quieres leer otro artículo acerca de cómo enfría un cubito de hielo (No enfría porque está frío, sino porque se derrite) no te pierdas esta otra entrada:




Buenisimo me encanta esta web
No dejan de repetir en las noticias que al derretirse el hielo aumenta el nivel del mar. Hacía falta esta explicación gracias!
Acaba de decir que si bien una masa de hielo flotante no afecta al nivel del agua, el hielo que se derrite que se encuentra sobre tierra firme si. La Antártida por ejemplo es un continente cubierto completamente por hielo, pero este hielo no flota sobre el océano, sino que descansa sobre tierra firme. Por lo tanto, si se derrite el hielo y/o se desprende algún fragmento de hielo al océano, incrementará el nivel del agua… creo que queda claro de que SÍ aumenta el nivel del mar…
exacto!
es incorrecto, solo es verdadero suponiendo Fuerza de empuje igual al Peso. Sin embargo en el caso de los iceberg, el empuje es mayor que el peso, esto permite que se tenga un volumen fuera del líquido. Todo el volumen de la parte superior del iceberg no está ejerciendo ningún desplazamiento. Si el área se modifica y se sumerge todo el hielo provocando E=W o bien E<W, la masa de iceberg ingresa al agua, y sucederá un aumento del nivel. ¿Cuánto? Subirá el nivel del agua con un aumento de volumen tanta fracción de hielo se encontrase rebasando la superficie libre del agua
Buenas Gerard, te comento;
No comprendo realmente por qué dices que la fuerza (entiendo que de arquímedes) no es igual al Peso. Por segunda Ley de Newton, el sumatorio de fuerzas es igual a la aceleración. Si no hay un equilibrio de fuerzas entonces el iceberg:
-Saldría volando hacia el cielo si el empuje es mayor al peso (caso que planteas)
-Se sumergería hacia el fondo, cosa que obviamente no sucede
Si tú sumerges, o fuerzas que se sumerja todo el iceberg, por supuesto que aumenta el nivel del agua. De hecho, la fuerza que tendrías que aplicar sería equivalente al “peso del agua que coincide con el volumen de iceberg que inicialmente en reposo estaba fuera pero ahora está forzado dentro”. En ese caso el equilibrio de fuerzas lo garantizas forzando que se sumerja. En el momento que dejases de aplicar la fuerza, el empuje sería mayor y el iceberg saldría hacia arriba “saltando”, lo que proporcionaría un estado transitorio con oleaje que finalizaría con la posición del iceberg en reposo
Quedó claro que el área sumergida ocupa el mismo espacio, pero no quedó claro si el área no sumergida aria que se derrame
Una duda.
El agua helada en la superficie de la tierra, de dónde salió?. Si es por evaporación de origen, ese volumen se resta de ahí. Si nieva en el Himalaya y luego se derrite todo. Es el volumen que se resto al evaporarse.
Interesante el artículo.
Un saludo.
Buenas Jose;
Todo el agua helada proviene de que en algún momento llovió ergo provino de evaporación de las diferentes masas de agua. Si, constantemente el agua de la superficie de mares y oceanos se evapora y por lo tanto “”””disminuye””” el nivel del mar. No obstante, paralelamente agua de lluvias anteriores vuelve a océanos y mares, manteniendo un ciclo más o menos estables. El nivel del mar actual es al equilibrio que se ha llegado entre evaporación y precipitación (y otros muchísimos factores). Si comienza a hacer más calor, se evaporará más agua (y lloverá más, proporcionalmente), y sobre todo se derritirá a mayor velocidad el hielo continental, añadiendo por lo tanto un volumen extra aumentando así el nivel del mar hasta que se llegase a un cierto punto de equilibrio.