La resolución de las Ecuaciones de Navier-Stokes es uno de los problemas del milenio recompensado por 1 millón de euros. Estas ecuaciones no son más que la aplicación de los principios de conservación de masa, movimiento y energía a un fluido. Son tan importantes porque su resolución implicaría un conocimiento absoluto de cómo un fluido se va a mover partiendo de unas condiciones iniciales y un gran uso que se le podría dar es el de por ejemplo dar previsiones meteorológicas exactas.
Sin embargo, el movimiento de un fluido es tan caótico que las ecuaciones adquieren una gran complejidad en su resolución y sólo pueden resolverse numéricamente o analíticamente por medio de muchas simplificaciones e idealizaciones del fluido.
En este artículo voy a desarrollar desde 0 (bueno, partiendo de conceptos medios de física) la obtención de dichas ecuaciones empleando cierto rigor físico-matemático y empleando como siempre la matemática para describir la realidad. Además, voy a seguir un desarrollo enfocado a su utilidad práctica en problemas de ingeniería de universidad, buscando una forma final que coincida con lo que se ve en clase y no sea excesivamente compleja.
Descripción Lagrangiana y Euleriana
En primer lugar es importantísimo saber que hay dos modos de describir el movimiento de un fluido. Mediante la descripción Lagrangiana, las partículas del fluido son seguidas una a una y de manera independiente a medida que estas se mueven. Como si fueran canicas muy muy pequeñas.
Por otra parte, bajo la descripción Euleriana, se fija un volumen de control (fluido contenido en un tramo de tubería por ejemplo) y se analiza en conjunto las características del fluido que fluye en su interior.
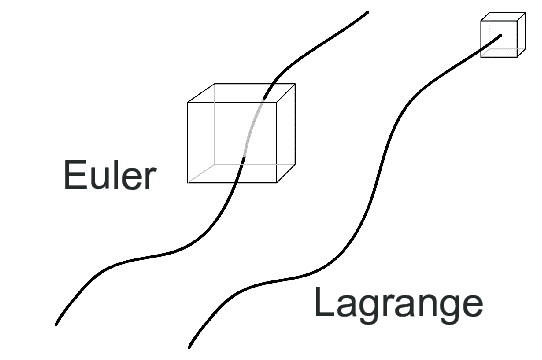
Es necesario combinar ambos puntos de vista porque para poder aplicar las Leyes de Newton al fluido debemos de considerar el movimiento independiente de las partículas (lagrangiana) mientras que la observación y medición del comportamiento macroscópico del fluido se realiza tomando volúmenes de control (euleriana).
Descripción Lagrangiana
Seguimos una partícula de fluido en su movimiento. Partiendo de unas condiciones iniciales \( \left \{ \vec{r}_{0} , t_{0} \right \}\) y las fuerzas externas, empleando las ecuaciones de la dinámica podríamos obtener la evolución de la posición de la partícula con una formulación tal que \(\vec{r} = \vec{r}(t;\vec{r}_{0},t_{0})\)
Una vez conocida la posición de cada una de las partículas, podemos definir el valor de una magnitud en un punto del fluido como \( F=F( \vec{r}(t;\vec{r}_{0},t_{0}) ,t)\) que será la magnitud asociada a la partícula estudiada.
Descripción Euleriana
Ahora nos centramos en describir las propiedades de un fluido alrededor de una zona centrada en \(\vec{x}\) en un tiempo t. De esta forma, el valor de una magnitud expresada según esta descripción como campo viene dada por \(F=F(\vec{x},t)\)
Unión de ambas descripciones
Para que ambas descripciones o modelos sean válidos, debe de haber una equivalencia en los valores de \(F\) cuando \(\vec{x} = \vec{r}\) en el mismo instante de tiempo \(t\), es decir, se estudie el mismo punto del fluido:
\( F( \vec{r}(t;\vec{r}_{0},t_{0}) ,t) = F(\vec{x},t) \ cuando \ \vec{x}=\vec{r} (t;\vec{r}_{0},t_{0}) \)
Si aplicamos la derivada de dicha función con respecto al tiempo:
\(\dfrac{d}{dt} \left [ F ( \vec{r}(t;\vec{r}_{0},t_{0}) ,t) \right ] = \dfrac{\partial F}{\partial t} + \dfrac{\partial F}{\partial r_{1}} \cdot \dfrac{\partial r_{1} }{\partial t} + \dfrac{\partial F}{\partial r_{2}} \cdot \dfrac{\partial r_{2} }{\partial t} + \dfrac{\partial F}{\partial r_{3}} \cdot \dfrac{\partial r_{3} }{\partial t} = \dfrac{d}{dt} \left [ F ( \vec{x} ,t) \right ] \)
Recordatorio de matemáticas: si tenemos una función de la forma \(f \left (x(t),t \right )=2x(t) + t\) con \(x(t)=t^{2}\), y la queremos derivar con respecto a \(t\), podemos sustituir el valor de \(t\) en la \(x\) y derivarla por completo con respecto a \(t\) o aplicar la regla de la cadena con derivadas parciales
- \(\dfrac{df}{dt} = \dfrac{d}{dt} [2 t^{2} + t] = 4t +1\)
- \(\dfrac{df}{dt} = \dfrac{\partial f}{\partial t} + \dfrac{\partial f}{\partial x} \cdot \dfrac{\partial x}{\partial t} = 1 + 2t \cdot 2 = 4t + 1 \)
Teniendo en cuenta que \(\vec{x} = \vec{r}\) y sabiendo que \(\dfrac{dr_{1}}{dt} = u_{1}\) (la derivada temporal de la posición en una coordenada es igual a la velocidad instantánea en dicha coordenada), definimos la siguiente relación:
\(\dfrac{D}{Dt} F (\vec{x},t) = \dfrac{\partial F}{\partial t} + \dfrac{\partial F}{\partial r_{1}} \cdot u_{1} + \dfrac{\partial F}{\partial r_{2}} \cdot u_{2} + \dfrac{\partial F}{\partial r_{3}} \cdot u_{3} = \dfrac{\partial F}{\partial t} + \vec{u} \cdot \vec{\bigtriangledown} F\)
Siendo \(\dfrac{D}{Dt}\) definida como la derivada temporal material de la descripción Euleriana de un campo fluido, equivalente a la derivada temporal total \(\dfrac{d}{dt}\) de la descripción Lagrangiana que expresa la variación temporal total de una magnitud que se desplaza en el tiempo. Es decir, que la derivada temporal total \(\dfrac{d}{dt}\) se emplea cuando hablamos de partículas, y la derivada temporal material \(\dfrac{D}{Dt}\) cuando hablamos de volúmenes.
Teorema de Transporte de Reynolds
El teorema de transporte de Reynolds se emplea para describir la derivada temporal de integrales sobre volúmenes de control que varían con el tiempo. Es una extensión tridimensional del Teorema fundamental del Cálculo.
Antes de nada haré una aclaración sobre los 3 tipos de volúmenes de control con los que trabajaremos:
- Volumen variable arbitrario \(V^{*}(t)\): Volumen de control de forma arbitraria (no tiene por qué coincidir con el volumen fluido por completo) y que se mueve de manera arbitraria con velocidad en sus paredes \(\vec{b}\). Es necesario escribir las ecuaciones aplicadas a un volumen de control arbitrario para poder extrapolarlas a cualquier problema real.
- Volumen material \(V(t)\): Volumen de control que coincide en todo momento con el volumen de fluido inicial con el que se define deformándose y desplazándose con él. Es muy útil porque dentro de él se conservan las magnitudes y por lo tanto sirve de partida para definir las ecuaciones de conservación.
- Volumen fijo \(V\): Volumen de control inmóvil en el cual la velocidad relativa del fluido es la del propio fluido. Es una simplificación del volumen arbitrario y es el que se emplea en problemas debido a su simplicidad e independencia temporal.
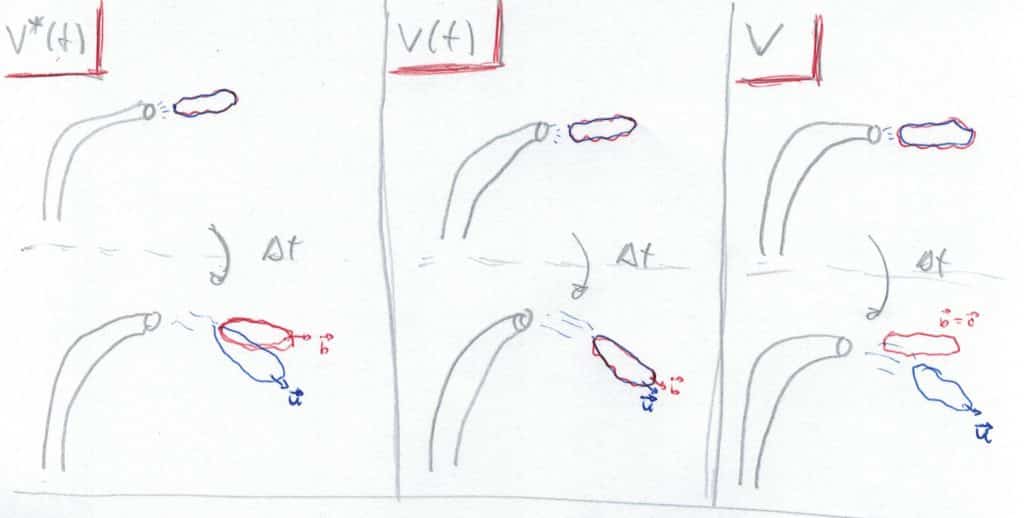
Vamos a suponer un volumen de control \(V^{*}(t)\) cerrado por una superficie continua cerrada \(A ^{*} (t)\) que coincide en el instante de tiempo \(t\) con un volumen fluido \(V(t)\) . Tras un instante de tiempo \(\bigtriangleup t\), el volumen \(V ^{*} (t)\) se desplaza con una velocidad en las paredes del volumen de valor \(\vec{b}\). Su normal exterior se define como \(\vec{n}\).
Comenzamos describiendo la derivada temporal de la integral de la magnitud en el volumen de control \(V ^{*} (t)\) en términos de límites:
\( \displaystyle \dfrac{d}{dt} \int_{ V ^{*} (t) } F(\vec{x},t) dV = lim_{\bigtriangleup t\to 0} \dfrac{1}{\bigtriangleup t} \cdot \left \{ \int_{ V ^{*} (t+ \bigtriangleup t ) } F(\vec{x},t + \bigtriangleup t ) dV – \int_{ V ^{*} (t) } F(\vec{x},t) dV \right \}\)
1)Hacemos un desarrollo de Taylor truncado al primer término de la función \(F\):
\( F(\vec{x},t + \bigtriangleup t ) = F(\vec{x},t) + \dfrac{\partial F}{\partial t} \cdot \bigtriangleup t\)
2) Definimos \(\bigtriangleup V ^{*} = V ^{*} (t+ \bigtriangleup t ) – V ^{*} (t ) \) y separamos la integral introduciendo el desarrollo anterior:
\(\displaystyle \int_{ V ^{*} (t+ \bigtriangleup t ) } F(\vec{x},t + \bigtriangleup t ) dV = \int_{ V ^{*} (t+ \bigtriangleup t ) } \left ( F(\vec{x},t) + \dfrac{\partial F}{\partial t} \cdot \bigtriangleup t \right ) dV =\) \(= \displaystyle \int_{ V ^{*} (t) } F(\vec{x},t ) dV + \int_{ V ^{*} (t) } \dfrac{\partial F}{\partial t} \bigtriangleup t \ dV + \int_{ \bigtriangleup V ^{*} } F(\vec{x},t ) dV + \int_{ \bigtriangleup V ^{*} } \dfrac{\partial F}{\partial t} \bigtriangleup t \ dV \)3) Introducimos el desarrollo en la ecuación inicial:
\( \displaystyle \frac{d}{dt} \int_{V^{*}(t)} F(\vec{x},t) dV = \lim_{\Delta t \to 0} \frac{1}{\Delta t} \left\{ \int_{V^{*}(t)} F(\vec{x},t) dV + \int_{V^{*}(t)} \frac{\partial F}{\partial t} \Delta t \, dV + \right . \\ \) \( \displaystyle \left . + \int_{\Delta V^{*}} F(\vec{x},t) dV + \int_{\Delta V^{*}} \frac{\partial F}{\partial t} \Delta t \, dV – \int_{V^{*}(t)} F(\vec{x},t) dV \right\} \)Quedando:
\( \displaystyle \dfrac{d}{dt} \int_{ V ^{*} (t) } F(\vec{x},t) dV = \\ lim_{\bigtriangleup t\to 0} \dfrac{1}{\bigtriangleup t} \cdot \left \{ \int_{ V ^{*} (t) } \dfrac{\partial F}{\partial t} \bigtriangleup t \ dV + \int_{ \bigtriangleup V ^{*} } F(\vec{x},t ) dV + \int_{ \bigtriangleup V ^{*} } \dfrac{\partial F}{\partial t} \bigtriangleup t \ dV \right \}\)4) En un intervalo de tiempo \(\bigtriangleup t\), el \(\bigtriangleup V\) que se produce es equivalente al “flujo de volumen” que entra/sale del pedazo de superficie \(dA\) de forma que
\(dV=\vec{b} \cdot \vec{n} \cdot \bigtriangleup t \cdot dA\)

Introduciendo en la integral:
\(\displaystyle \int_{\bigtriangleup V^{*}} F(\vec{x},t) dV = \oint_{A^{*}} F(\vec{x},t) \cdot \vec{b} \cdot \vec{n} \cdot \bigtriangleup t \cdot dA\)
5)Introduciendo este cambio en la ecuación principal queda:
\( \displaystyle \dfrac{d}{dt} \int_{ V ^{*} (t) } F(\vec{x},t) dV = \\ \displaystyle lim_{\bigtriangleup t\to 0} \dfrac{1}{\bigtriangleup t} \cdot \left \{ \int_{ V ^{*} (t) } \dfrac{\partial F}{\partial t} \bigtriangleup t \ dV + \\ \displaystyle \oint_{A^{*}} F(\vec{x},t) \cdot \vec{b} \cdot \vec{n} \cdot \bigtriangleup t \cdot dA + \oint_{A^{*}} \dfrac{\partial F}{\partial t} \cdot \vec{b} \cdot \vec{n} \cdot \bigtriangleup t^{2} \cdot dA \right \}\)
Quedando la relación definida como:
\(\displaystyle \boxed{ \dfrac{d}{dt} \int_{ V ^{*} (t) } F(\vec{x},t) \ dV = \int_{ V ^{*} (t) } \dfrac{\partial F}{\partial t} \ dV + \oint_{A^{*}} F(\vec{x},t) \cdot \vec{b} \cdot \vec{n} \ dA }\)
Aplicada sobre una magnitud \(F\) contenida en el volumen de control variable \(V^{*}(t)\). Lo que expresa la relación es que la derivada de una magnitud dentro de un recinto variable es igual a la variación de la magnitud con el recinto fijo + lo que varía debido a la variación del recinto (o lo que “fluye” de la magnitud).
Se observa que si \(\vec{b}=\vec{0}\), el volumen no varía y por lo tanto se cumple que \(\displaystyle \dfrac{d}{dt} \int = \int \dfrac{\partial}{ \partial t}\)
Conservación de la masa
La ecuación de conservación de la masa para una partícula viene dada por:
\(\dfrac{dm}{dt} = 0 \)
Supongamos un volumen material \(V(t)\) que se mueve y deforma a la par que el fluido de forma que \(\vec{b}=\vec{u}\). Sustituyendo el valor de masa por la integral de la densidad en el volumen de fluido (se conserva la masa total del fluido) la conservación de la masa queda:
\(\displaystyle \dfrac{d}{dt} \int_{V(t)} \rho \ dV = 0 \)
Aplicando el Teorema de Transporte de Reynolds obtenemos la ecuación de la conservación de la masa en un volumen material:
\(\displaystyle \dfrac{d}{dt} \int_{V(t)} \rho \ dV = \int_{V(t)} \dfrac{\partial \rho}{\partial t} \ dV + \oint_{A(t)} \rho \cdot (\vec{u} \cdot \vec{n}) \ dA = 0 \)
Sin embargo, puede ser conveniente expresar la ecuación para volúmenes de control que se muevan a nuestra conveniencia. Para ello, aplicaremos el Teorema de Transporte de Reynolds a un volumen genérico \(V^{*}(t)\) que se mueve a velocidad \(\vec{b}\) (obsérvese que ya no podemos igualarla a cero porque ya no es nuestra “bola” de fluido que se mantiene a masa constante sino un volumen de control arbitrario):
\(\displaystyle \dfrac{d}{dt} \int_{V^{*}(t)} \rho \ dV = \int_{V ^{*} (t)} \dfrac{\partial \rho}{\partial t} \ dV + \oint_{A ^{*} (t)} \rho \cdot (\vec{b} \cdot \vec{n}) \ dA \rightarrow \)
\(\displaystyle \rightarrow \int_{V ^{*} (t)} \dfrac{\partial \rho}{\partial t} \ dV = \dfrac{d}{dt} \int_{V^{*}(t)} \rho \ dV – \oint_{A ^{*} (t)} \rho \cdot (\vec{b} \cdot \vec{n}) \ dA \)
Si en el instante de estudio \(t\) consideramos que el volumen de control y el volumen de fluido a estudiar coinciden pero que se mueven de manera diferente, podemos hacer la siguiente equivalencia:
\( \displaystyle \int_{V (t)} \dfrac{\partial \rho}{\partial t} \ dV =\int_{V ^{*} (t)} \dfrac{\partial \rho}{\partial t} \ dV \)
\( \displaystyle \oint_{A (t)} \rho \cdot (\vec{u} \cdot \vec{n}) \ dA = \oint_{A ^{*} (t)} \rho \cdot (\vec{u} \cdot \vec{n}) \ dA \)
(Es decir, que la integral en el recinto \(X(t)\) y \(X^{*}(t)\) toma el mismo valor porque el recinto es el mismo)
Introduciendo el desarrollo en términos del Teorema de Transporte de Reynolds para el volumen de control de movimiento indeterminado dentro de la expresión de la ecuación de la conservación de la masa en un volumen material llegamos a la expresión final:
\(\displaystyle \boxed{\dfrac{d}{dt} \int_{V^{*}(t)} \rho \ dV + \oint_{A ^{*} (t)} \rho \cdot (\vec{u} – \vec{b}) \cdot \vec{n} \ dA =0}\)
Resultando esta la ecuación general integral de conservación de la masa para un volumen de control arbitrario.
Se observa que si el volumen de control se mueve con el fluido, entonces \(\vec{b}=\vec{u}\) y nuestra ecuación vuelve a reducirse a la de conservación de la masa para \(V(t)\) igualada a cero. Si el volumen de control no se desplaza, es decir, \(\vec{b}=\vec{0}\) entonces podemos meter dentro de la integral la derivada y obtenemos la siguiente fórmula:
\(\displaystyle \int_{V} \dfrac{\partial \rho}{\partial t} \ dV + \oint_{A} \rho \cdot (\vec{u} \cdot \vec{n}) \ dA = 0 \)
Resumen ecuaciones integrales
La ecuación para un volumen de control que se mueve de la misma forma que el fluido (volumen material) es:
\(\displaystyle \dfrac{d}{dt} \int_{V(t)} \rho \ dV = \int_{V(t)} \dfrac{\partial \rho}{\partial t} \ dV + \oint_{A(t)} \rho \cdot (\vec{u} \cdot \vec{n}) \ dA = 0 \)
La ecuación para un volumen de control que no se mueve es:
\(\displaystyle \int_{V} \dfrac{\partial \rho}{\partial t} \ dV + \oint_{A} \rho \cdot (\vec{u} \cdot \vec{n}) \ dA = 0 \)
La ecuación general para un volumen de control que se mueve de manera indeterminada es:
\(\displaystyle \dfrac{d}{dt} \int_{V^{*}(t)} \rho \ dV + \oint_{A ^{*} (t)} \rho \cdot (\vec{u} – \vec{b}) \cdot \vec{n} \ dA =0\)
Forma diferencial
Podemos eliminar las integrales para, a partir de una ecuación fundamental como la conservación de la masa, obtener una relación entre las variables implicadas. La ecuación diferencial de conservación de la masa puede obtenerse empleando el Teorema de la divergencia de Gauss en el volumen material:
\(\displaystyle \int_{V(t)} \dfrac{\partial \rho}{\partial t} \ dV + \int_{V(t)} \vec{\bigtriangledown} (\rho \cdot \vec{u}) \ dV = 0 = \int_{V(t)} \left ( \dfrac{\partial \rho}{\partial t} + \vec{\bigtriangledown} (\rho \cdot \vec{u}) \right )\ dV \iff \\ \)\( \iff \boxed{\dfrac{\partial \rho}{\partial t} + \vec{\bigtriangledown} (\rho \cdot \vec{u}) = 0}\)
Si desarrollamos esta última ecuación obtenemos:
\( \dfrac{\partial \rho}{\partial t} + \vec{u} \cdot \vec{\bigtriangledown} \rho + \rho \cdot \vec{\bigtriangledown} \cdot \vec{u} = 0\)
Agrupando la definición de derivada material expuesta anteriormente se obtiene la forma compacta:
\(\boxed{\dfrac{D \rho}{D t} + \rho \cdot \vec{\bigtriangledown} \cdot \vec{u} = 0} \)
Si la densidad de las partículas del fluido no varía en el flujo (flujo incompresible) entonces \( \dfrac{D \rho}{D t} =0\) y la ecuación se reduce a:
\( \boxed{\vec{\bigtriangledown} \cdot \vec{u} = 0 }\)
Antes vamos a aclarar algunos conceptos:
- Un flujo a densidad constante es un flujo en el que todas las partículas fluidas tienen la misma densidad constante y por lo tanto la derivada material de la densidad es nula.
- Un flujo incompresible es un flujo en el que puede haber partículas de diferente densidad pero que cada una de ellas mantiene su densidad constante, siendo también la derivada material de la densidad nula.
Por lo tanto, un flujo a densidad constante siempre es un flujo incompresible, pero un flujo incompresible no implica que la densidad del flujo sea constante. Un claro ejemplo se da en el flujo de un río, donde las capas más inferiores de agua presentan levemente una mayor densidad debido a la presión del agua que las superiores pero aún así podemos estudiarlo como un flujo incompresible.
Conservación de cantidad de movimiento
La ecuación de conservación de cantidad de movimiento para una partícula es
\(\displaystyle \dfrac{d}{dt} (m \cdot \vec{v}) = \sum \vec{F}\)
Si aplicamos dicha ecuación al volumen material separando las fuerzas por unidad de superficie (actúan sobre las paredes del fluido) y las de volumen (actúan uniformemente sobre todo el fluido (sólo se considera la gravedad a nivel didáctico)) tenemos la siguiente ecuación integral:
\(\displaystyle \dfrac{d}{dt} \int_{V(t)} (\rho \cdot \vec{u}) \ dV = \oint_{A(t)} \vec{t_{n}} \ dA + \int_{V(t)} \rho \vec{g} \ dV\)
Aplicando el Teorema de Transporte de Reynolds al volumen material:
\( \displaystyle \int_{V(t)}\dfrac{\partial (\rho \cdot \vec{u}) }{\partial t} \ dV + \oint_{A(t)} \rho \cdot \vec{u} \cdot (\vec{u} \cdot \vec{n}) \ dA= \oint_{A(t)} \vec{t_{n}} \ dA + \int_{V(t)} \rho \vec{g} \ dV \)
Si queremos aplicarla a un volumen de control arbitrario \(V^{*}(t)\) que se mueve a velocidad \(\vec{b}\) se sigue un procedimiento análogo al seguido para la expresión de la conservación de masa y se llega a la siguiente expresión general:
\(\displaystyle \boxed{\dfrac{d}{dt} \int_{V^{*}(t)} (\rho \cdot \vec{u}) \ dV + \oint_{A^{*}(t)} \rho \cdot \vec{u} \cdot (\vec{u} – \vec{b}) \cdot \vec{n} \ dA = \oint_{A^{*}(t)} \vec{t_{n}} \ dA + \int_{V^{*}(t)} \rho \vec{g} \ dV}\)
Si el volumen de control es fijo, entonces seguimos el mismo razonamiento y la ecuación queda:
\( \displaystyle \int_{V}\dfrac{\partial (\rho \cdot \vec{u}) }{\partial t} \ dV + \oint_{A} \rho \cdot \vec{u} \cdot (\vec{u} \cdot \vec{n}) \ dA= \oint_{A} \vec{t_{n}} \ dA + \int_{V} \rho \vec{g} \ dV \)
Esfuerzos sobre fluidos
En esta subsección voy a desarrollar el término \(\displaystyle \oint_{A(t)} \vec{t_{n}} \ dA \) de las fuerzas de superficie.
Un fluido va a sufrir dos tipos de esfuerzos superficiales: esfuerzos normales (presión) y esfuerzos tangenciales (viscosidad). Como este término expresa las fuerzas externas ejercidas sobre el fluido, en general en las caras libres la fuerza que actúa es la presión y en las caras en contacto con el sólido la fuerza que actúa es la de rozamiento o viscosidad. Definiendo las fuerzas superficiales por medio de una matriz que caracteriza el estado tensional, el integrando quedaría como \(\vec{t_{n}} = \underline{\sigma} \cdot \vec{n}\) tal que \(\sigma = -P \cdot \underline{I} + \underline{\tau}\)
Donde \(P\) es el valor de la presión y \(\underline{\tau}\) es la parte desviadora del estado tensional definida como:
\(\tau_{ij} = \mu \left ( \dfrac{\partial u_{i}}{\partial x_{j}} + \dfrac{\partial u_{j}}{\partial x_{i}} \right ) + \lambda \dfrac{\partial u_{k}}{\partial x_{k}} \delta_{ij} \)
Donde \(\mu\) es el coeficiente de viscosidad dinámico y \(\lambda\) el segundo coeficiente de viscosidad. Estas son unas constantes medidas experimentalmente y dicha ecuación se obtiene de la relación entre tensión-deformación cuya deducción se presenta en este artículo.
El valor de dicha fuerza suele ser indeterminado y variable a lo largo de la superficie del fluido en contacto con el sólido. Sin embargo, bajo ciertas condiciones, podemos trabajar directamente con su integral, es decir, la resultante de las fuerzas que el sólido ejerce sobre el fluido. O, lo que es más común y se pide en ejercicios, podemos despejar la fuerza que el fluido ejerce sobre el sólido. Esto se desarrolla en el ejemplo del cohete al final del artículo. No es necesario tampoco saber detalladamente cómo se descompone el término \(\displaystyle \oint_{A(t)} \vec{t_{n}} \ dA \) pero viene bien una idea básica de qué representa para poder comprender los desarrollos y simplificaciones posteriores.
Forma diferencial de la ecuación de cantidad de movimiento
Partiendo de la ecuación integral del volumen material:
\( \displaystyle \int_{V(t)}\dfrac{\partial (\rho \cdot \vec{u}) }{\partial t} \ dV + \int_{A(t)} \rho \cdot \vec{u} \cdot (\vec{u} \cdot \vec{n}) \ dA \ = \int_{A(t)} \underline{\sigma} \cdot \vec{n} \ dA + \int_{V(t)} \rho \vec{g} \ dV \)Aplicando el Teorema de la divergencia de Gauss:
\( \displaystyle \int_{V(t)} \left [ \dfrac{\partial (\rho \cdot \vec{u}) }{\partial t} + \vec{\bigtriangledown} ( \rho \cdot \vec{u} \cdot \vec{u} ) – \vec{\bigtriangledown} \underline{\sigma} – \rho \vec{g} \right ] \ dV =0 \\\) \(\displaystyle \rho \cdot \dfrac{\partial \vec{u}}{\partial t} + \vec{u} \cdot \dfrac{\partial \rho}{\partial t} + \vec{u} \cdot \vec{\bigtriangledown} (\rho \cdot \vec{u})+ \rho \cdot \vec{u} \vec{\bigtriangledown} \vec{u} = \vec{\bigtriangledown} \underline{\sigma} + \rho \vec{g}\)(Se cancela el segundo y tercer término porque es \(\vec{u}\) multiplicando a la ecuación de conservación de la masa)
\( \vec{u} \cdot \left(\dfrac{\partial \rho}{\partial t} + \vec{\bigtriangledown} (\rho \cdot \vec{u}) \right) = 0\)
Desarrollando el término de \(\sigma_{ij}\) obtenemos la ecuación diferencial de conservación de cantidad de movimiento en notación de índices:
\(\displaystyle \boxed{\rho \cdot \dfrac{\partial u_{i}}{\partial t} + \rho \cdot u_{j} \cdot \dfrac{\partial u_{i}}{\partial x_{j}} = – \dfrac{\partial P}{\partial x_{i}} + \mu \dfrac{\partial}{\partial x_{j}} \left ( \dfrac{\partial u_{i}}{\partial x_{j}} + \dfrac{\partial u_{j}}{\partial x_{i}} \right ) + \lambda \dfrac{\partial}{\partial x_{i}} \left ( \dfrac{\partial u_{j}}{\partial x_{j}} \right ) + \rho \cdot g_{i}}\)
Ecuaciones de Navier-Stokes
Las ecuaciones de conservación de masa y cantidad de movimiento definidas hasta ahora sin hacer ninguna simplificación del fluido son:
Masa
\( \dfrac{\partial \rho}{\partial t} + \dfrac{\partial}{\partial x_{i}} (\rho \cdot u_{i}) = 0 \)Cantidad de movimiento
\(\displaystyle \rho \cdot \dfrac{\partial u_{i}}{\partial t} + \rho \cdot u_{j} \cdot \dfrac{\partial u_{i}}{\partial x_{j}} = – \dfrac{\partial P}{\partial x_{i}} + \mu \dfrac{\partial}{\partial x_{j}} \left ( \dfrac{\partial u_{i}}{\partial x_{j}} + \dfrac{\partial u_{j}}{\partial x_{i}} \right ) + \lambda \dfrac{\partial}{\partial x_{i}} \left ( \dfrac{\partial u_{j}}{\partial x_{j}} \right ) + \rho \cdot g_{i}\)Si consideramos un flujo a densidad constante o incompresible, entonces la ecuación de conservación de masa se reduce a \(\dfrac{\partial u_{i}}{\partial x_{i}} = 0\) de forma que de la ecuación de conservación de cantidad de movimiento desaparecen los siguientes términos:
- \(\displaystyle \mu \dfrac{\partial}{\partial x_{j}} \left ( \dfrac{\partial u_{j}}{\partial x_{i}} \right ) = \mu \dfrac{\partial}{\partial x_{i}} \left ( \dfrac{\partial u_{j}}{\partial x_{j}} \right ) = 0\)
- \(\displaystyle \lambda \dfrac{\partial}{\partial x_{i}} \left ( \dfrac{\partial u_{j}}{\partial x_{j}} \right ) = 0\)
De esta forma, para un flujo a densidad constante las ecuaciones de Navier-Stokes se reducen a:
\( \dfrac{\partial u_{i}}{\partial x_{i}} = 0 \)
\(\displaystyle \rho \cdot \dfrac{\partial u_{i}}{\partial t} + \rho \cdot u_{j} \cdot \dfrac{\partial u_{i}}{\partial x_{j}} = – \dfrac{\partial P}{\partial x_{i}} + \mu \dfrac{\partial^{2} u_{i}}{\partial x_{j}^{2}} + \rho \cdot g_{i}\)
Que, empleando vectores y definiendo la viscosidad cinemática como \(\nu = \dfrac{\mu}{\rho}\):
\(\displaystyle \dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} + \dfrac{\partial w}{\partial z} =0\)
\(\displaystyle \dfrac{\partial u}{\partial t} + u \cdot \dfrac{\partial u}{\partial x} + v \cdot \dfrac{\partial u}{\partial y} + w \cdot \dfrac{\partial u}{\partial z} = – \dfrac{1}{\rho} \dfrac{\partial P}{\partial x} + \nu \left ( \dfrac{\partial^{2} u}{\partial x^{2}} + \dfrac{\partial^{2} u}{\partial y^{2}} + \dfrac{\partial^{2} u}{\partial z^{2}} \right )+ g_{x}\)
\(\displaystyle \dfrac{\partial v}{\partial t} + u \cdot \dfrac{\partial v}{\partial x} + v \cdot \dfrac{\partial v}{\partial y} + w \cdot \dfrac{\partial v}{\partial z} = – \dfrac{1}{\rho} \dfrac{\partial P}{\partial y} + \nu \left ( \dfrac{\partial^{2} v}{\partial x^{2}} + \dfrac{\partial^{2} v}{\partial y^{2}} + \dfrac{\partial^{2} v}{\partial z^{2}} \right )+ g_{y}\)
\(\displaystyle \dfrac{\partial w}{\partial t} + u \cdot \dfrac{\partial w}{\partial x} + v \cdot \dfrac{\partial w}{\partial y} + w \cdot \dfrac{\partial w}{\partial z} = – \dfrac{1}{\rho} \dfrac{\partial P}{\partial z} + \nu \left ( \dfrac{\partial^{2} w}{\partial x^{2}} + \dfrac{\partial^{2} w}{\partial y^{2}} + \dfrac{\partial^{2} w}{\partial z^{2}} \right )+ g_{z}\)
Si nos fijamos en los términos del sistema de ecuaciones diferenciales, como es lógico son 4 ecuaciones (físicamente independientes entre sí) para 4 incógnitas, siendo “””posible””” matemáticamente obtener una solución para las 4 incógnitas:
\(u(\vec{x},t), \ v(\vec{x},t), \ w(\vec{x},t), \ P(\vec{x},t)\)
Sin embargo, hasta la fecha nadie ha sido capaz de resolverlas por completo. Es un sistema de ecuaciones diferenciales tan complejo que involucra tantas variables que la única forma de poder obtener una solución es numéricamente y muchas veces haciendo simplificaciones. Es por medio de simplificaciones (flujo estacionario y por lo tanto desaparecen las derivadas temporales, flujo ideal y así desaparece el término con viscosidad, problema bidimensional y desaparece la componente correspondiente a z…) que se pueden obtener soluciones analíticas fáciles y aplicadas a los problemas típicos de mecánica de fluidos. Hay aún así soluciones más complejas que involucran transformaciones y cambios de variables como los problemas de Stokes e incluso formulaciones famosas como la de Bernoulli donde se simplifican enormemente y son las que básicamente se aplican en problemas de universidad.
Falta aún así una quinta ecuación: la ecuación de conservación de energía. Es otra ecuación diferencial más que involucra términos termodinámicos como la entalpía, el calor, la temperatura… Entonces… ¿Por qué no la he utilizado? ¿Me sobra?
La cosa está en que es una ecuación más que involucra una nueva variable hasta ahora no analizada: la temperatura. Esta ecuación añade una complicación aún mayor porque términos como la viscosidad dependen a su vez de la temperatura. Afortunadamente, su importancia no es tan alta para analizar problemas típicos de fluidos de universidad (sí que lo es para cálculos precisos obviamente) y por lo tanto es mejor no meternos en profundidad e ignorar el efecto de la temperatura por ahora.
A continuación una foto resumen por parte de la NASA de dichas ecuaciones al completo sin la simplificación de densidad constante y teniendo en cuenta la ecuación de conservación de la energía

Ejemplos de problemas de fluidos y su resolución con las ecuaciones
En este apartado analizaré situaciones reales que se simplifican para ser analizadas mediante las ecuaciones simplificadas y se suelen estudiar en mecánica de fluidos. Antes de nada debo recordar que existen 2 formulaciones: una integral y otra diferencial, y usar una u otra depende de lo que nos pidan.
- Para empezar, la ecuación diferencial nos sirve exclusivamente para calcular u obtener la expresión analítica de alguna de las 4 incógnitas presentes en las ecuaciones diferenciales: perfil de velocidades o presión.
- La ecuación integral nos sirve para obtener el resto de magnitudes que se derivan de una integración de dichas variables y que nos proporcionan generalmente un valor de “resultante“. Para obtener el caudal (integración de velocidad x área) o la fuerza (integración de acciones externas) empleamos la formulación integral.
Además, con respecto al tema de las fuerzas, hay que destacar que el término asociado a las fuerzas bajo la formulación se refiere a las fuerzas ejercidas SOBRE el fluido, lo que por acción-reacción se traduce en fuerzas que el fluido ejerce sobre el cuerpo en contacto con sentido opuesto. Esto es esencial en los problemas como veremos a continuación.
Ejemplo diferencial: flujo entre láminas infinitas
Un primer ejemplo es el de un flujo estacionario (derivada con respecto al tiempo nula) entre un canal de 2 láminas infinitas del cual nos piden obtener el perfil de velocidades. Se asume un gradiente de presiones en dirección al eje del movimiento constante de manera que en régimen permanente se garantiza un flujo estacionario \(\dfrac{\partial P}{\partial x} = – \bigtriangleup P\).
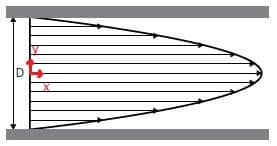
Como las láminas son infinitas, se asume que no hay velocidad con respecto al plano de simetría (coordenada perpendicular a la pantalla z (w)), pudiendo simplificar el problema a 2 dimensiones: x (u) e y (v) y eliminando los términos con derivada asociada a la coordenada z. Se simplifica por lo tanto también el término de gravedad. Además se asume densidad constante. Partiendo de las ecuaciones elimino términos nulos:
\(\displaystyle \dfrac{\partial u}{\partial x} + \dfrac{\partial v}{\partial y} + =0\)
\(\displaystyle u \cdot \dfrac{\partial u}{\partial x} + v \cdot \dfrac{\partial u}{\partial y} = – \dfrac{1}{\rho} \dfrac{\partial P}{\partial x} + \nu \left ( \dfrac{\partial^{2} u}{\partial x^{2}} + \dfrac{\partial^{2} u}{\partial y^{2}} \right )\)
\(\displaystyle u \cdot \dfrac{\partial v}{\partial x} + v \cdot \dfrac{\partial v}{\partial y} = – \dfrac{1}{\rho} \dfrac{\partial P}{\partial y} + \nu \left ( \dfrac{\partial^{2} v}{\partial x^{2}} + \dfrac{\partial^{2} v}{\partial y^{2}} \right )\)
Como además el problema es infinitamente simétrico con respecto al eje \(x\) (da igual donde estudiemos el perfil de velocidades que será el mismo en cualquier punto del canal) las derivadas con respecto a \(x\) también se anulan (excepto el gradiente de presiones constante que es quien empuja el flujo o más bien evita que la viscosidad lo frene). Quedan por lo tanto estas ecuaciones:
\(\displaystyle \dfrac{\partial v}{\partial y} =0\)
\(\displaystyle v \cdot \dfrac{\partial u}{\partial y} = \dfrac{1}{\rho} \bigtriangleup P + \nu \dfrac{\partial^{2} u}{\partial y^{2}} \)
\(\displaystyle 0 = – \dfrac{1}{\rho} \dfrac{\partial P}{\partial y} \)
Gracias al término de la primera ecuación podemos simplificar la última ecuación quedando el siguiente sistema de ecuaciones diferenciales:
\(\displaystyle \dfrac{\partial v}{\partial y} =0 \rightarrow v=cte=v_{0}\)
\(\displaystyle v \cdot \dfrac{\partial u}{\partial y} = \dfrac{1}{\rho} \bigtriangleup P + \nu \dfrac{\partial^{2} u}{\partial y^{2}} \)
\(\displaystyle 0 = – \dfrac{1}{\rho} \dfrac{\partial P}{\partial y} \rightarrow P=P(x)=P_{0} – (\bigtriangleup P) \cdot x \)
Es en este momento cuando usamos las condiciones de contorno:
- Al haber un plano de simetría justo en la mitad entre placas, la velocidad vertical en ese punto debe de ser nula (o no habría simetría)
- Todas las componentes de la velocidad deben de ser nulas en los extremos (paredes) por continuidad.
De esta forma, como sabemos que la velocidad vertical es constante según las ecuaciones y que en el medio (o incluso extremos) del flujo esta es nula, la única solución posible es que \(v=v_{0}=0\), simplificando la segunda ecuación:
\(\displaystyle \mu \dfrac{\partial^{2} u}{\partial y^{2}} = – \bigtriangleup P \rightarrow u(y)= – \left (\dfrac{1}{2 \cdot \mu} \bigtriangleup P \right ) \cdot y^{2} + A \cdot y + B \)
Si sustituimos los valores en los extremos podemos obtener el valor de los parámetros:
- \(u(-D/2)=0 \rightarrow – \left (\dfrac{1}{8 \cdot \mu} \bigtriangleup P \right ) \cdot D^{2} – A \dfrac{D}{2}+ B =0 \)
- \(u(D/2)=0 \rightarrow – \left (\dfrac{1}{8 \cdot \mu} \bigtriangleup P \right ) \cdot D^{2} + A \dfrac{D}{2}+ B =0 \)
Si sumamos las ecuaciones podemos despejar \(B\) y posteriormente \(A\) , que toman los siguientes valores:
\(B= \left (\dfrac{1}{8 \cdot \mu} \bigtriangleup P \right ) \cdot D^{2} \) \(A= 0 \)Y el perfil de velocidades resulta:
\(\displaystyle u(y)= \left (\dfrac{1}{8 \cdot \mu} \bigtriangleup P \right ) \cdot \left (D^{2} – 4y^{2} \right ) \)
Completamente realista y respetando las condiciones de contorno:
- Se anula la velocidad en los extremos y además el máximo se alcanza a mitad del canal \(y=0\)
- El valor de la velocidad es proporcional al gradiente de presiones e inversamente proporcional al término de viscosidad, es decir, a mayor “fuerza” que empuje el fluido más velocidad adquiere y a menor viscosidad menos se “frena”.
Este problema tiene muchas variaciones. El mismo flujo pero en vez de con un gradiente de presiones constante “externo”, un gradiente de presiones constante debido al término de gravedad. Un canal inclinado de manera que afecta parcialmente la gravedad. Un canal en el cual una de las placas se desplaza a una cierta velocidad (problema de Couette). Un canal que en vez de dos placas infinitas el canal es un tubo infinito (problema de Poiseuille), etc.
Ejemplo integral: cohete
Tenemos un cohete muy simplificado consistente en una entrada de aire, una cámara de combustión y una salida de aire que se encuentra en un banco de pruebas (el motor no se mueve, está quieto).
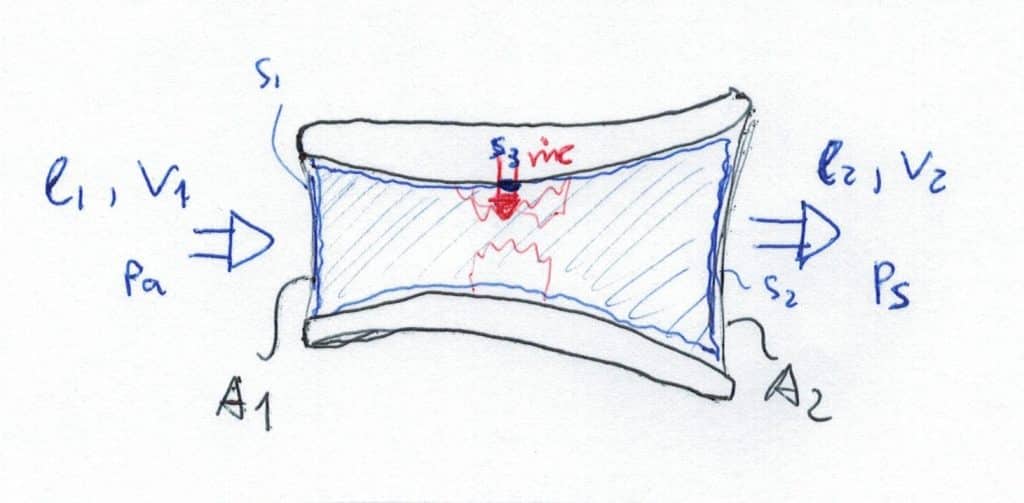
Queremos calcular el valor del empuje que suministra el motor partiendo de datos conocidos. El cohete tiene un área de entrada de aire \(A_{1}\) a densidad \(\rho_{1}\) y presión igual a la presión atmosférica \(P_{a}\) a velocidad media \(v_{1}\) perpendicular a la sección. Se produce una combustión tras inyectar una masa por unidad de tiempo de combustible igual a \(\dot{m}_{c}\) que varía las propiedades del gas haciéndolo salir a una presión \(P_{s}\) en un área \(A_{2}\) con densidad \(\rho_{2}\) y velocidad media perpendicular a la sección \(v_{2}\).
Se asume flujo estacionario \(\dfrac{\partial}{\partial t}=0\) y efecto de la gravedad despreciable sobre el gas.
Como es una resultante emplearemos las ecuaciones integrales para obtener la relación entre los caudales de entrada y salida y el empuje ejercido por el motor. Las ecuaciones para un volumen de control que no se desplaza son:
\(\displaystyle \oint_{A} \rho \cdot (\vec{u} \cdot \vec{n}) \ dA =0\) \( \displaystyle \oint_{A} \rho \cdot \vec{u} \cdot (\vec{u} \cdot \vec{n}) \ dA= \oint_{A} \vec{t_{n}} \ dA \)Desarrollando la ecuación de conservación de masa:
\( \int_{S_{1}} \rho \cdot \vec{u} \cdot \vec{n} \ dA + \int_{S_{2}} \rho \cdot \vec{u} \cdot \vec{n} \ dA + \int_{S_{3}} \rho \cdot \vec{u} \cdot \vec{n} \ dA = -\rho_{1} v_{1} A_{1} + \rho_{2} v_{2} A_{2} – \dot{m}_{c} =0 \rightarrow \)\( \rightarrow \boxed{ \rho_{2} v_{2} A_{2} = \rho_{1} v_{1} A_{1} + \dot{m}_{c}} \)
Para analizar el término de las fuerzas antes descomponemos la integral. La resultante que se ejerce sobre la “carcasa” del motor es equivalente a la integral de las fuerzas de superficie que se ejercen sobre ella. Por lo tanto:
\(\displaystyle \vec{R}_{S} = \oint_{ {S}_{s} } \vec{t_{n}} \ dA = \int_{ {S}_{s_{libre}} } \vec{t_{n}} \ dA + \int_{ {S}_{s_{f}} } \vec{t_{n}} \ dA = \int_{ {S}_{s_{libre}} } \vec{t_{n}} \ dA – \int_{ {S}_{f_{s}} } \vec{t_{n}} \ dA \)Introduciendo los términos apropiados en la ecuación integral de conservación de cantidad de movimiento:
\( \displaystyle \int_{A} \rho \cdot \vec{u} \cdot (\vec{u} \cdot \vec{n}) \ dA= \oint_{A} \vec{t_{n}} \ dA = \int _{ {S}_{f_{libre}} } \vec{t_{n}} \ dA + \int _{ {S}_{f_{s}} } \vec{t_{n}} \ dA = \) \( \displaystyle = \underbrace{ \int _{ {S}_{f_{libre}} } \vec{t_{n}} \ dA + \int_{ {S}_{s_{libre}} } \vec{t_{n}} \ dA} \ – \ \vec{R}_{S} = \oint _{ {S}_{libre} } \vec{t_{n}} \ dA \ – \ \vec{R}_{S} \)La suma de ambas superficies constituye un volumen cerrado que es sometido a presión atmosférica \(P_{a}\) en toda su superficie excepto en la tobera de salida, donde la presión existente es la presión de salida de gases \(P_{s}\)
Aplicamos entonces el principio de superposición para dividir la integral en 2 integrales: una en el volumen cerrado donde sólo hay presión atmosférica constante y otra en la que la única presión existente es la aplicada sobre la tobera de salida igual a \(P_ {s}-P_{a}\)
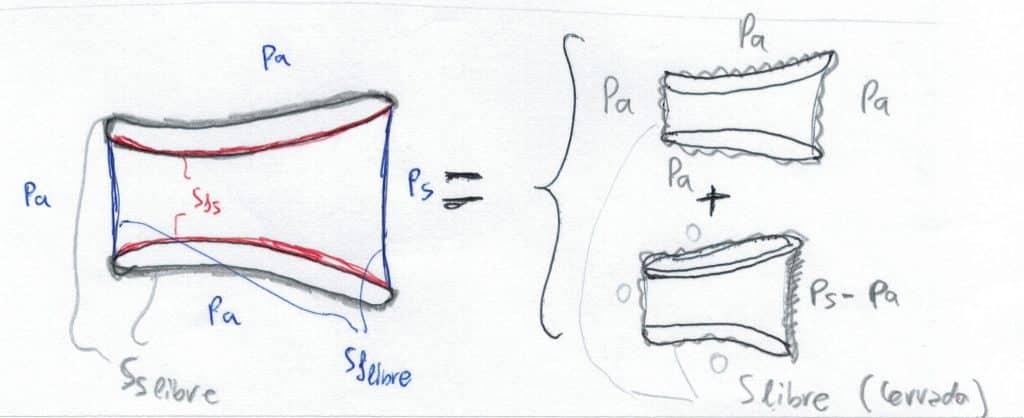
Por el Teorema de la Divergencia de Gauss podemos hacer 0 la integral sobre la superficie cerrada \(\displaystyle \oint_{S_{libre}} P_{a} \cdot \vec{n} \ dA = 0\) y el término que sobrevive es \(\displaystyle \int_{S_{2}} (P_{s}-P_{a}) \cdot \vec{n} \ dA\)
La ecuación queda:
\( \displaystyle \oint_{A} \rho \cdot \vec{u} \cdot (\vec{u} \cdot \vec{n}) \ dA= \int_{S_{2}} (P_{s}-P_{a}) \cdot \vec{n} \ dA – \vec{R}_{S} \)
\( \displaystyle \vec{R}_{S} = \int_{S_{f_{1}}} \rho \cdot \vec{u} \cdot (\vec{u} \cdot \vec{n}) \ dA + \int_{S_{f_{2}}} \rho \cdot \vec{u} \cdot (\vec{u} \cdot \vec{n}) \ dA + \int_{S_{2}} (P_{s}-P_{a}) \cdot \vec{n} \ dA = \\ = \displaystyle – \rho_{1} \cdot A_{1} \cdot v^{2}_{1} \cdot \vec{i} + \rho_{2} \cdot A_{2} \cdot v^{2}_{2} \cdot \vec{i} – (P_{s}-P_{a}) \cdot A_{2} \cdot \vec{i}\)Sustituyendo la equivalencia entre flujos de la ecuación de conservación de masa y definiendo el empuje \( T \) como la fuerza positiva opuesta a la eyección del fluido llegamos a la expresión final:
\( \displaystyle -R_{x} = \boxed{T = \rho_{1} \cdot A_{1} \cdot v_{1} ( \underbrace{ v_{2} – v_{1} }_{gas} ) + \underbrace{ \dot{m}_{c} \cdot v_{2}}_{comb} + \underbrace{(P_{s}-P_{a})}_{presion} \cdot A_{2} }\)
Es decir, que el empuje se genera por:
- Acelerar el caudal de gas inicial que entra por la tobera: yo aumento su velocidad hacia la derecha y el gas me “empuja” a mi hacia la izquierda.
- Acelerar el caudal de combustible que entra en la tobera desde una velocidad inicial que suponemos nula.
- La diferencia de presión entre la presión en la cara de salida de gases y la presión atmosférica a la que se encuentra “el resto del motor” y que lo empuja hacia la izquierda como si hubiese algún tipo de repulsión.

![Demostración de la ecuación de Bernoulli [Fluidos] Portada Bernoulli](https://ingenieriabasica.es/wp-content/uploads/2020/08/Portada-Bernoulli-200x200.jpg)