
Introducción
En esta entrada hablaremos acerca de Leonhard Euler. Me parece el matemático más influyente y de los más importantes que ha visto el mundo, y por ello le dedico el puesto honorífico de la primera entrada dedicada a grandes científicos. Su obra ha trascendido a lo largo de la historia y ha sido fundamental para el desarrollo de otros grandes matemáticos como Lagrange o Laplace, del cual se conoce la siguiente cita:
Lean a Euler, lean a Euler, él es el maestro de todos nosotros
Pierre Simon Laplace
Biografía
Primeros años y eduación
Leonhard Paul Euler nació en Basilea, Suiza, el 15 de abril de 1707. Su padre, Paul Euler, era un pastor calvinista y amigo de Johann Bernoulli, que en ese momento era ya considerado el principal matemático europeo, y que ejercería una gran influencia sobre el joven Leonhard.
A la edad de 13 años se matriculó en la Universidad de Basilea y en 1723 (16 años) recibió el título de maestro de Filosofía. En aquella época Euler se dedicaba a estudiar teología, griego y hebreo, siguiendo los deseos de su padre, y con la vista puesta en llegar a ser también pastor. Además, Euler daba clases particulares todos los sábados por la tarde con Johann Bernoulli, quien descubrió rápidamente el increíble talento para las matemáticas de su nuevo alumno. Johann Bernoulli intervino para convencer a Paul Euler de que Leonhard estaba destinado a ser un gran matemático.

Desarrollo profesional
Cuatro años más tarde fue invitado personalmente por Catalina I para convertirse en asociado de la Academia de Ciencias de San Petersburgo, donde coincidió con otro miembro de la familia Bernoulli, Daniel, a quien en 1733 relevó en la cátedra de matemáticas.
En el año 1735 Euler sufrió una fiebre casi fatal, y tres años después de dicho acontecimiento quedó prácticamente ciego del ojo derecho.

Posteriormente, en 1741 marchó a Alemania para aceptar un cargo en la Academia de Berlín. Allí vivió 25 años y escribió más de 380 artículos. Sin embargo, a pesar de su gran aportación, fue obligado finalmente a dejar Berlín. El motivo de esto fue, en parte, un conflicto de personalidad entre el matemático y el propio rey Federico, que llegó a ver a Euler como una persona muy poco sofisticada y a estar descontento con sus habilidades prácticas de ingeniería.
Últimos años
Euler más tarde sufrió cataratas en su ojo sano, el izquierdo, lo que le dejó prácticamente ciego pocas semanas después de haber sido diagnosticadas. A pesar de ello, sus problemas de visión no afectaron a su productividad intelectual, dado que lo compensó con su gran capacidad de cálculo mental y su memoria fotográfica. Por ejemplo, Euler era capaz de repetir la Eneida de Virgilio desde el comienzo hasta el final sin dudar en ningún momento.
Euler calculaba sin esfuerzo aparente, como los hombres respiran, o como las águilas se sostienen en el aire.
François Arago
En 1766 Euler aceptó una invitación para volver a la Academia de San Petersburgo y pasar allí el resto de su vida.
Finalmente, el 18 de septiembre de 1783, Euler falleció en la ciudad de San Petersburgo tras sufrir un accidente cerebrovascular. El matemático y filósofo francés Nicolas de Condorcet escribió su elogio funerario para la Academia francesa:
… dejó de calcular y de vivir.
Nicolas de Condorcet

Su legado
Euler trabajó prácticamente en todos los ámbitos de las matemáticas: geometría, cálculo, trigonometría, álgebra, teoría de números, además de física continua, teoría lunar y otras áreas de la física. Adicionalmente, hizo aportaciones relevantes a la lógica matemática con su diagrama de conjuntos.
Es considerado el matemático más prolífico de la historia. Su actividad de publicación fue incesante (un promedio de 800 páginas de artículos al año en su época de mayor producción, entre 1727 y 1783), y una buena parte de su obra completa está sin publicar. Se le considera el ser humano con mayor número de trabajos y artículos en cualquier campo del saber, solo equiparable a Gauss.
Contribución a la notación matemática
- Popularizó el uso de la letra \(\pi\) para relacionar la longitud de una circunferencia y su diámetro. Para más información acerca del número pi visita esta entrada
- Introdujo la letra \(i\) para denotar el número complejo \(\sqrt{-1}\).
- Popularizó el uso de las letras a,b,c para denotar los lados de un triángulo y A,B,C para los vértices opuestos a cada lado.
- Introdujo el símbolo \(\sum\) de sumatorio.
- Empleo de f(x) para denotar a una función f que depende de x. Además, dió una definición para el concepto de función: «Una función de una magnitud variable es cualquier expresión analítica formada por la cantidad variable y por cantidades constantes»
El número de Euler
Identidad de Euler
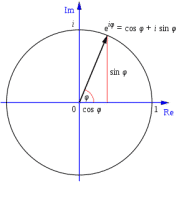
La identidad de Euler es un caso especial de la fórmula de Euler en el que se involucran 5 de los números más importantes de las matemáticas: \(i,\pi,e,0 \ y \ 1\), y tiene la siguiente forma:
\(e^{\pi i}+1=0\)Función \(\phi\) de Euler
Si n es un número entero positivo, entonces \(\phi(n)\) se define como el número de enteros positivos menores o iguales a n y coprimos con n, es decir, se puede definir como:
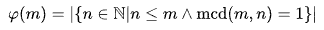
Generando como valor la cantidad de números que cumpen dicha condición. Para más información: Enlace a Wikipedia
Series. Desarrollos en serie. Infinitos
El problema de Basilea
El Problema de Basilea es un famoso problema de teoría de números, planteado por primera vez por Pietro Mengoli, y resuelto por Leonhard Euler en 1735. Consistía en encontrar la suma exacta de los inversos de los cuadrados de los enteros positivos, esto es, la suma exacta de la serie infinita:
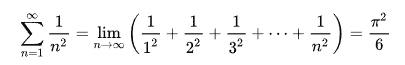
Que obtuvo siguiendo un desarrollo en serie de \(\frac{sin(x)}{x}\) e igualando términos. Para el desarrollo: Demostración en Wikipedia
Euler trabajó numerosos desarrollos en serie y estudió los límites y sumatorios infinitos, comprendiendo cuando un número es muy grande o muy pequeño, de manera que numerosas ecuaciones podían simplificarse sin perder generalidad. Todo esto junto con el estudio de las funciones se encuentra en su obra: Introductio in analysin infinitorum (1748) . En dicha obra también se estableció el tratamiento analítico de las funciones trigonométricas en Europa, definiéndolas como series infinitas presentadas en las llamadas «Fórmulas de Euler».
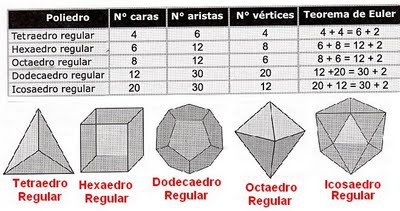
Fórmula de Euler para poliedros convexos
Un poliedro es un cuerpo geométrico de 3 dimensiones cuyas caras son planas y encierran un volumen finito. Los segmentos que unen dichas caras se denominan aristas y los puntos donde se cortan las aristas se denominan vértices.
Un poliedro convexo es un poliedro tal que, si tomamos dos puntos cualesquiera de su volumen, podemos unirlos mediante un segmento que esté contenido en el poliedro. Es decir, que no presenta agujeros ni pliegues.
Para cualquier poliedro convexo, Euler formuló un teorema que siempre se cumple:
\(C+V=A+2\)Siendo:
C=Número de caras
V=Número de vértices
A=Número de aristas
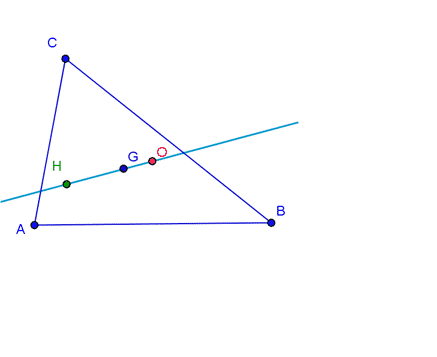
Recta de Euler
Leonhard Euler demostró que en cualquier triángulo el ortocentro, el circuncentro y el baricentro se encuentran alineados. A dicha recta que une los puntos la denominamos recta de Euler. Además demostró que, si un triángulo es equilátero, entonces el circuncentro, baricentro y ortocentro coinciden en el mismo punto. Demostración en Wikipedia
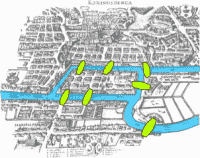
Teoría de grafos
El problema de los puentes de Königsberg
Otras contribuciones
Sudoku
Sorprendentemente, Euler sentó las bases del popular juego que conocemos actualmente como Sudoku. Si bien no lo inventó como tal ni su objetivo era convertirlo en un pasatiempo, creó un sistema de probabilidades para representar una serie de números en filas, columnas y celdas sin que ninguno de ellos se repitiera, generando 9 celdas únicas.
En 1970 la editorial Math Puzzles and Logic Problems publicó por primera vez un pasatiempos basado en dicho sistema. No obstante quedó en el olvido.
En 1984 el periódico japonés Monthly Nikolist publicó una sección de pasatiempos llamada Sūji wa dokushin ni kagiru («Los números deben estar solos»). El nombre se abrevió a Sūdoku (sū = número, doku = solo) y más tarde se popularizó en todo el mundo.

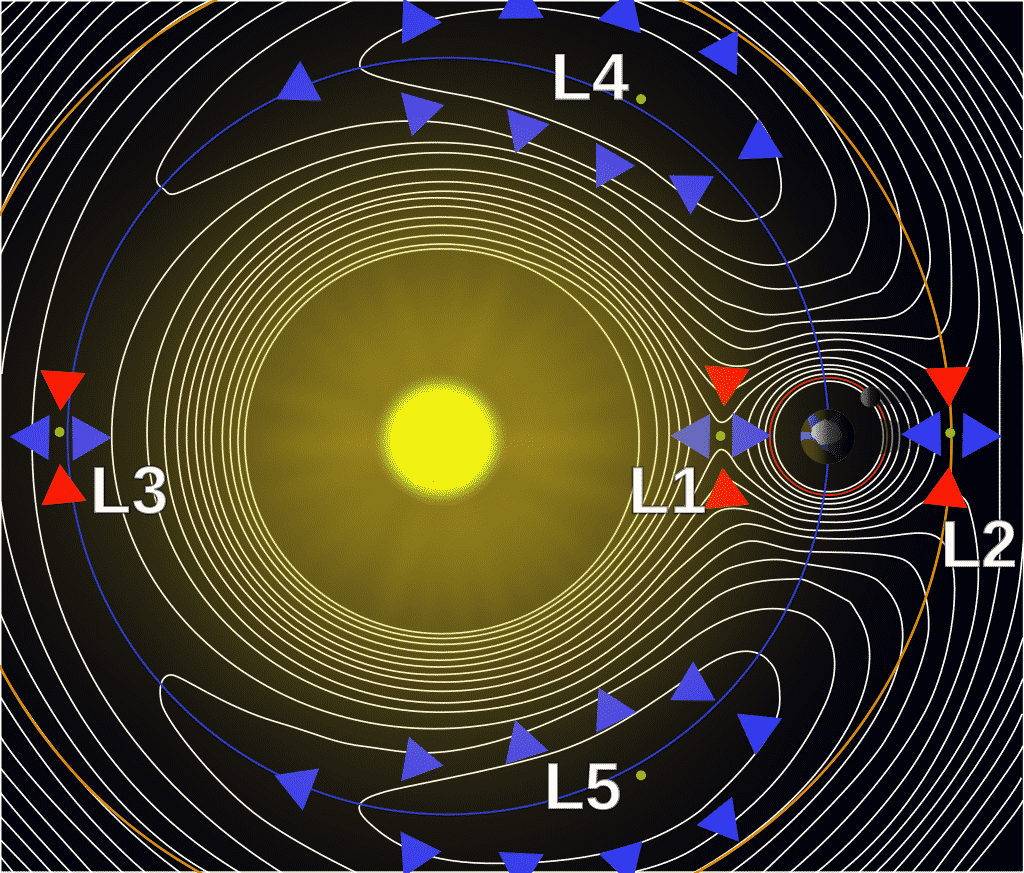
Problema de los 3 cuerpos
El problema de los tres cuerpos consiste en determinar, en cualquier instante, las posiciones y velocidades de tres cuerpos, de cualquier masa, sometidos a la atracción gravitacional mutua. Para ello se parten de unas condiciones iniciales en posición y velocidad, siendo 18 valores; sus 3 coordenadas de posición [3×3] y las tres componentes de su velocidad [3×3].
Lamentablemente su solución es caótica (Un pequeño cambio en las condiciones iniciales supone una solución completamente diferente) y no lineal, siendo necesario el empleo de desarrollos en serie y/o métodos computacionales.
El problema de los tres cuerpos restringido o de Euler es una simplificación del problema, suponiendo que la masa de uno de los cuerpos es despreciable y que las órbitas son aproximadamente circulares (Suficientemente válido para el sistema Sol-Tierra-Luna). En el problema circular, existen cinco puntos de equilibrio llamados puntos de Lagrange, en los cuales el tercer cuerpo se puede encontrar teóricamente estacionario respecto a los otros dos.



gracias