
¡Buenas! En este artículo vamos a hablar de una figura matemática muy curiosa: La Trompeta de Gabriel.
Esta trompeta no es ni mucho menos la que porta la Fama, el icono de la Universidad de Sevilla, ni tampoco produce sonido, aunque es aún mas sorprendente.
El Cuerno o Trompeta de Gabriel
La Trompeta de Gabriel (también llamada trompeta de Torricelli, en honor al físico y matemático Evangelista Torricelli, quien la ideó) es una figura geométrica de revolución que se obtiene al girar alrededor del eje X la función \(f(x)=\frac{1}{x}\) desde x=1 a \(\infty\)
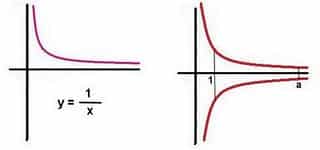
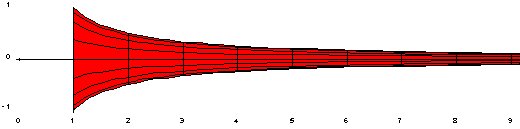
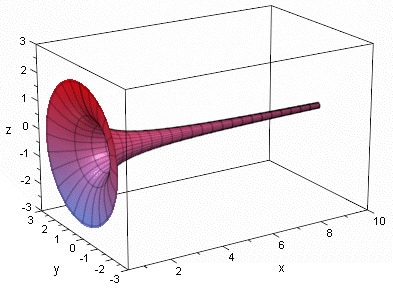

El nombre de Gabriel hace referencia a dicho arcángel, el cual toca la trompeta que anuncia el Día del Juicio Final, asociando de este modo lo infinito con lo finito.
Cálculo de volumen y área: Integrales
Para calcular el área y el volumen de esta figura geométrica vamos a emplear como es lógico las integrales.
Antes de poder integrar necesitamos dos cosas: Una función y un recinto de integración. Primero hallamos una parametrización en coordenadas polares para la región x,y,z (En polares, al ser de revolución es más cómodo).
Tenemos: \(\left\{ \begin{matrix} x = x & 1\leq x\leq \infty \\ y = r\cdot\cos(\theta) & 0\leq r \leq \frac{1}{x} \\ z = r\cdot\sin(\theta) & 0\leq \theta \leq 2\pi \\ \end{matrix} \right.\)
Siendo el jacobiano r:
\(\begin{vmatrix} \frac{\partial x}{\partial x} & \frac{\partial y}{\partial x} & \frac{\partial z}{\partial x}\\ \frac{\partial x}{\partial r} & \frac{\partial y}{\partial r} & \frac{\partial z}{\partial r}\\ \frac{\partial x}{\partial \theta} & \frac{\partial y}{\partial \theta} & \frac{\partial z}{\partial \theta} \end{vmatrix}\)=\(\begin{vmatrix} 1 & 0 & 0 \\ 0 & cos(\theta) & sen(\theta)\\ 0 & -r*sen(\theta) & r*cos(\theta) \end{vmatrix}\) = r
En Wikipedia, Wolfram, Brilliant… emplean el principio de Cavalieri para el cálculo del volumen y la superficie en una variable (Que, de hecho, fue el método que Torricelli empleó).. Sin embargo, he decidido emplear esta parametrización y el uso de integrales dobles y triples ya que son mucho más intuitivas y requieren menos fórmulas.
Cálculo de la superficie
Cuando queremos integrar en una superficie necesitamos 2 variables. Como sabréis, si lo que queremos es calcular las dimensiones de una región la cual es mismamente nuestra región de integración el integrando o función a integrar es 1 (Multiplicado por el jacobiano)
Nuestras variables son \(\theta\) y \(x\) ya que en el caso de la superficie nuestra r está fijo como \(r=\frac{1}{x}\) en todo momento.
\( S= \int_{1}^{\infty} \int_{0}^{2\pi} r d\theta dx = \int_{1}^{\infty} \int_{0}^{2\pi} \frac{1}{x} d\theta dx = \) \(= 2\pi \int_{1}^{\infty} \frac{1}{x} dx = 2\pi*[ln(\infty)-ln(1)]=2\pi ln(\infty)=\infty\)Observamos que obtenemos una integral impropia que genera un valor infinito para la superficie.
Cálculo del volumen
Cuando queremos integrar un volumen necesitamos 3 variables. Al igual que en el caso anterior, como lo que queremos integrar es nuestra propia región de integración, el jacobiano es el único integrando.
Nuestras variables son \(\theta\) , \(x\) y \(r\), ya que en este caso r va a ir variando entre 0 y \(\frac{1}{x}\) para rellenar el volumen.
\(V= \int_{1}^{\infty} \int_{0}^{\frac{1}{x}} \int_{0}^{2\pi} r d\theta dr dx =2\pi \int_{1}^{\infty} \int_{0}^{\frac{1}{x}} r dr dx = \) \(= 2\pi \int_{1}^{\infty} \frac{1}{2} \frac{1}{x^{2}} dx = \pi * -[\frac{1}{x}]_{1}^{\infty}=\pi * [1-\frac{1}{\infty}]=\pi\)Conclusiones
Descubrimos que el valor de la superficie es infinito mientras que el valor del volumen es finito y es ni más ni menos que el recurrente número pi.
La explicación que se da a este fenómeno o paradoja es el caso de querer pintar la trompeta.
Si intentamos pintar la superficie exterior con una capa de pintura uniforme no acabaríamos nunca porque la superficie, como hemos demostrado, es infinita.
No obstante, si intentamos pintar la superficie interior llegaría un momento en el que el hueco entre superficies es tan pequeño que prácticamente sería imposible pintarlas por dentro ya que se solaparían. De esta forma, si colocásemos verticalmente la trompeta y la llenásemos de pintura llegaría un momento en que comenzaría a rebosar la pintura debido a que hemos llenado su volumen. No se filtraría más pintura ya que, como hemos dicho antes, la distancia teórica entre superficies internas sería menor que el tamaño de las moléculas de pintura. Esta es la magia del infinito.
Por si lo estáis pensando: Está demostrado matemáticamente que no existe ninguna figura con área finita pero volumen infinito. Vaya, me he quedado con un artículo menos.



El amor de ella se encuentra al otro extremo de la trompeta…
JAJAJAJAJA F:(
literal
¿Y la curva de Koch?