💡La Paradoja de San Petersburgo💡

Ya sabéis que en este blog nos encantan las paradojas. La paradoja de la cuerda y el conejo, La paradoja del cumpleaños y La trompeta de Gabriel son ejemplos de paradojas ya enunciadas.

En esta ocasión vamos a analizar una paradoja basada en la estadística que no va a dejar indiferente a nadie.

Todo empezó con una inocente carta que un Bernoulli (Si, esa familia suiza que prácticamente ha estado presente en todos los ámbitos de las ciencias y conocida principalmente por La ecuación de Bernoulli) envió a un amigo planteándole el problema que veremos a continuación. La cosa es que cuando el propio autor intentó hallar la solución al problemita que él mismo había planteado se dió cuenta de que no fue capaz. Pasaron los años y el problema/paradoja se distribuyó entre las grandes mentes de San Petersburgo y no fue hasta 25 años después que se le pudo dar una solución. Es así como surge La Paradoja de San Petersburgo.

Enunciado de la Paradoja de San Petersburgo

El problema consiste en estimar, dada una apuesta con su correspondiente posible ganancia y riesgo, cuánto dinero sería justo que pagase el jugador por jugar.

El jugador paga un dinero por jugar y hace lo siguiente: Lanza una moneda varias veces hasta que salga cruz y cuenta los lanzamientos que ha empleado para que haya salido cruz. Si llamamos \(n\) al número de lanzamientos empleados, entonces el jugador recibe \(2^{n}\)€

• De esta forma, si en la primera tirada sale cruz -> Gana 2€
• Si sale cruz en la segunda tirada -> Gana 4€
• Si sale cruz en la tercera tirada -> Gana 8€
• …
• Si sale cruz en la tirada \(n\) -> Gana \(2^{n}\)€

Es decir, que en el momento que sale cruz el juego acaba y se paga el premio. Obviamente, cuanto más tarde en salir la cruz, mayor es la ganancia.

Una vez conoces el funcionamiento del juego, te pregunto. ¿Cuánto dinero estarías dispuesto a pagar por jugar una ronda?

Obviamente al ser mínimo 2€ el premio, esa es la mínima cantidad que intuitivamente deberíamos de pagar. Si ya nos ponemos más matemáticos, y como realmente hay un 50% de que fallemos la primera tirada, hay un 50% de que ganemos 4€ o más y por lo tanto es intuitivo pensar que 3€ seguiría siendo un precio justo pero aún bajo (50% de acabar ganando 2€ y 50% de acabar ganando 4€ o más).

Pero claro, ese “o más” es el problema. Y es que no tenemos que decir por qué cantidad nosotros jugaríamos (Porque en ese caso yo jugaría por 0.01€), sino por qué cantidad sería justo que jugásemos de forma que a la larga ni la banca ni tú perdáis incluyendo todos los posibles resultados.

Análisis del problema

Los más matemáticos lo tendrán claro. ¿Apuestas? ¿ROI? —–> Esperanza matemática, esperanza matemática, esperanza matemática…

Y obviamente lo que hay que hacer en este caso es calcular la esperanza matemática. Su definición y aplicaciones son esenciales en la estadística, pero para no extender mucho el artículo yo la definiría como una suma ponderada de probabilidades.

En nuestro caso en concreto, la variable aleatoria “Lanzamientos hasta que sale cruz” es una variable aleatoria discreta. Por ello, la esperanza matemática es igual a la suma de la probabilidad de cada posible suceso multiplicado por el premio del suceso.

Es decir, un sumatorio que englobe todas las posibles tiradas \(n\) en el que se sume la probabilidad de que salga X multiplicado por el dinero que se ganaría.

Por ejemplo, si yo tiro un dado tal que:

• Si sale el 1 o el 6 gano 1€
• Si sale cualquier otro número no gano nada

La esperanza matemática sería:

\(\frac{4}{6} \cdot 0 + \frac{2}{6} \cdot 1 = \frac{2}{6}\)

Es decir, de 1/3€ porque de media de cada 6 tiradas acertaría en 2 de ellas y por lo tanto el valor justo a pagar en ese juego sería de 1/3€ para que a la larga ni la banca ni yo perdamos de media. En la ruleta, por ejemplo, si hubiese 36 números el valor justo a pagar sería de 1/36€ porque si aciertas un número ganas x36 veces el valor apostado. Sin embargo, para que el negocio sea rentable y la banca gane añadieron el 0 verde, de forma que en la ruleta realmente la esperanza matemática es de 1/37€ , y por lo tanto de cada 1€ apostado a la ruleta a la larga te quedas con 0.97€ \( \left ( 1 \cdot \frac{36}{37} \right )\)€.

Volviendo a nuestro caso, la esperanza matemática se vuelve un sumatorio infinito puesto que yo puedo llegar a lanzar las monedas infinitas veces y que no salga cruz (Con obviamente una probabilidad infinitamente baja). La fórmula queda de esta forma:

\(E=\sum_{i=1}^{\infty} \frac{1}{2^{i}} \cdot 2^{i} = \sum \frac{1}{2} \cdot 2 + \frac{1}{4} \cdot 4 + \frac{1}{8} \cdot 8 \dots = \sum_{i=1}^{\infty} 1 = \infty\)

Al ser la ganancia inversamente proporcional a la probabilidad los sumandos son 1 y una suma infinita de 1 es igual a infinito.

La paradoja surge entonces porque siguiendo las directrices de la teoría de la decisión en estas condiciones sería justo apostar una cantidad infinita de dinero. Sin embargo, ninguna persona estaría dispuesta a jugar por más de 15-20€.

¿Qué es lo que falla entonces? ¿Las matemáticas dan un valor demasiado alto o es que nosotros subestimamos las ganancias?

Solución de La Paradoja de San Petersburgo

Más que una solución a este problema lo que se han desarrollado han sido explicaciones a la paradoja. Lo que está claro es que las matemáticas nunca fallan (Lo que falla quizás es la aplicación que les damos) y que el problema está bien planteado tal y como está. Entonces… ¿Qué sucede?

La explicación la obtuvo el propio Bernoulli 25 años después: La utilidad del dinero.

Cualquier incremento en riqueza, no importa cuan insignificante, siempre resultará en un incremento en utilidad que es inversamente proporcional a la cantidad de bienes ya poseídos. Los matemáticos, en su teoría, valoran el dinero en proporción a la cantidad del mismo; la gente con sentido común, en la práctica, lo valora en proporción a la utilidad que puede obtener de él.

Daniel Bernoulli, Academia de Ciencias de San Petersburgo (1938)

Es decir, que matemáticamente 500 millones de euros es el doble de 250 millones de euros. Sin embargo, para nosotros es prácticamente lo mismo porque nosotros miramos la utilidad. De hecho, lo que sucede en nuestro juego es que a medida que aumenta el premio la utilidad marginal tiende a cero. Pero sin embargo el valor de la apuesta crece linealmente hasta infinito.

No nos renta, por lo tanto, apostar una cantidad elevada de dinero para tener la posibilidad de recibir miles de millones de millones de euros.

¿Sigues sin estar de acuerdo con el juego? Te propongo un cambio: fijemos un número máximo de lanzamientos tal que si no ha salido cruz hasta ese momento no ganas nada.

Es decir, si fijamos el número máximo de lanzamientos en 3:

• Tienes un 50% de probabilidad de ganar 2€
• Tienes un 25% de probabilidad de ganar 4€
• Tienes un 12.5% de probabilidad de ganar 8€

Por lo tanto, la esperanza matemática se reduce a:

\(E=\sum_{i=1}^{3} \frac{1}{2^{i}} \cdot 2^{i} = \frac{1}{2} \cdot 2 + \frac{1}{4} \cdot 4 + \frac{1}{8} \cdot 8 = 1 + 1 + 1 = 3\)

Es decir, que bajo dichas condiciones, 3€ es un precio justo para jugar.

Pero… ¿Por qué es tan bajo en comparación con el caso anterior? Porque hay un 12.5% que se ha quedado en el aire. En el problema original ese 12.5% se iba dividiendo en porcentajes más pequeños que a su vez multiplicaban valores más grandes, de forma que si los lanzamientos no tienen límite el premio sería seguro. Si no estuviesen limitadas las apuestas en la ruleta con la Martingala ganaríamos siempre.

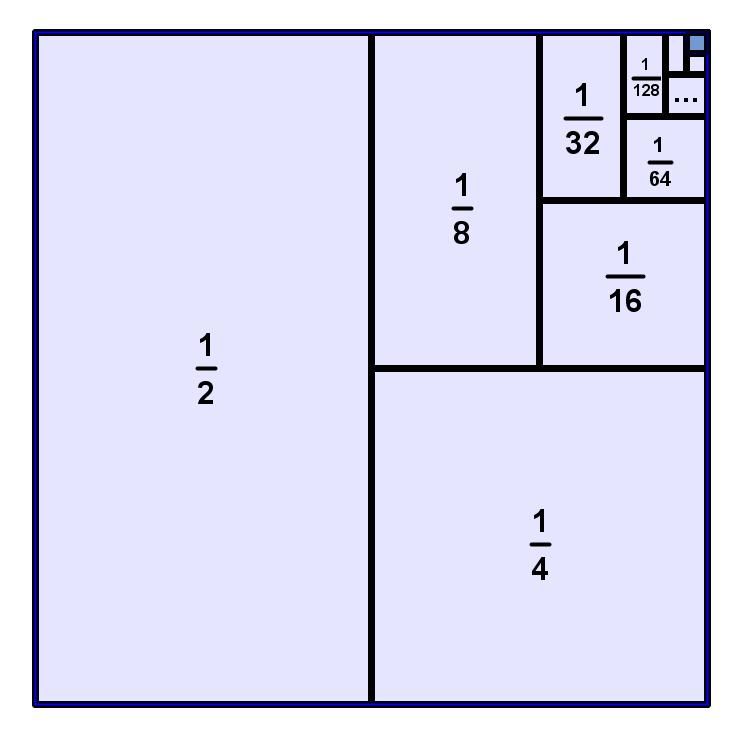
Pongamos por ejemplo el caso de que limitamos las apuestas a 20. Por lo tanto, la esperanza matemática nos diría que el precio justo a apostar serían 20€. ¿Caro? ¿Barato? La cosa es que a parte de tener la posibilidad de ganar 2€ o 4€ fácilmente (Al 75%), tenemos un 0.0001% aproximadamente de ganar 1 millón de euros. ¿Mucho? ¿Poco? Ahí están los números y su tamaño, tan difícil de medir para la mente humana, es de vital importancia.

Pongamos el ejemplo de estar dispuesto a pagar 250€ por jugar. Eso implicaría que sigue existiendo la posibilidad de ganar 1 millón de euros al 0.0001%, pero además surge una posibilidad, muy baja pero no nula, de ganar hasta \(1.8 \cdot 10^{75}\)€. Eso implicaría una montaña de euros de \(3.8 \cdot 10^{72}\) metros, lo que se traducirían en \(1.5 \cdot 10^{58}\) años luz, \(3 \cdot 10^{61}\) veces la distancia de la Tierra a Plutón, cuya masa serían \(1.35 \cdot 10^{73}\) kg, es decir, \(6.75 \cdot 10^{42}\) VECES la masa del Sol. Esto se parece a lo que le sucedió a un rey que subestimó las potencias del 2. Y podemos llegar a ganar ese dinero con sólo 250€.

Ufff, que dolor de cabeza. Con un milloncete de euros me conformo, ¿Para qué quiero más? El dinero comienza a perder utilidad… Y tú, ¿Hasta cuánto estarías dispuesto a apostar? Porque un número infinito de euros… es mucho, ¿No?

---

Simulaciones

Para poder ver realmente qué es lo que sucede y comprobar si la teoría se cumple realicé una serie de simulaciones del juego.

A continuación se muestran las gráficas con los resultados en las que destaca principalmente el precio justo por juego. Esto consiste simplemente en dividir la ganancia total entre el número de veces que se ha jugado.

Aparece también por ejemplo el premio máximo obtenido y en qué juego sucedió.

En caso de que no se puedan apreciar correctamente los números puede ampliarse la vista con la lupa (Ctrl+Rueda de ratón hacia arriba) o abrir la imagen en una pestaña nueva.

Juego sin límites

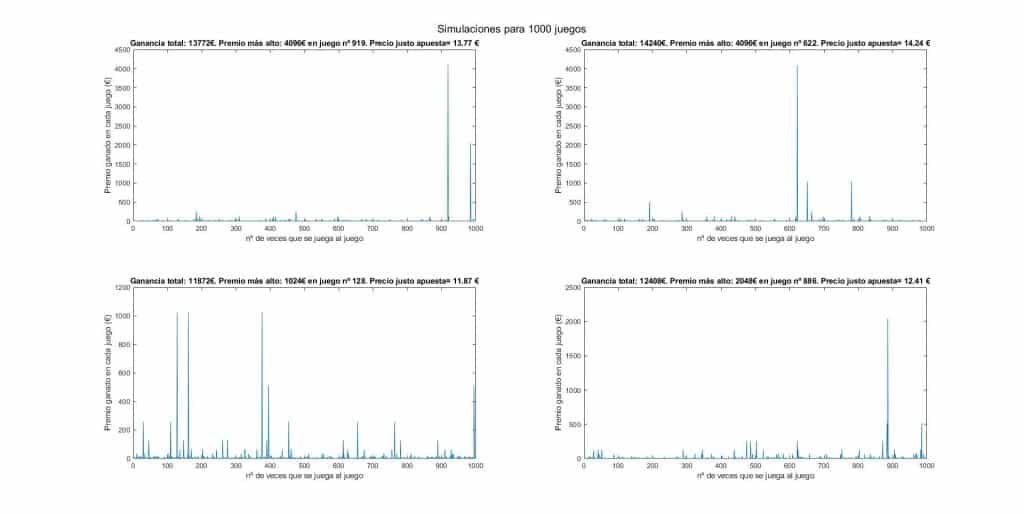
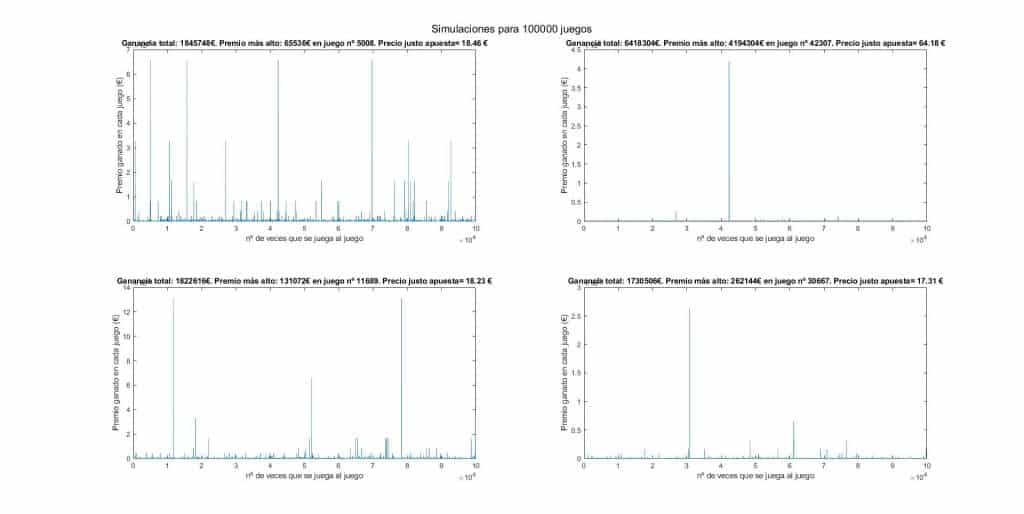
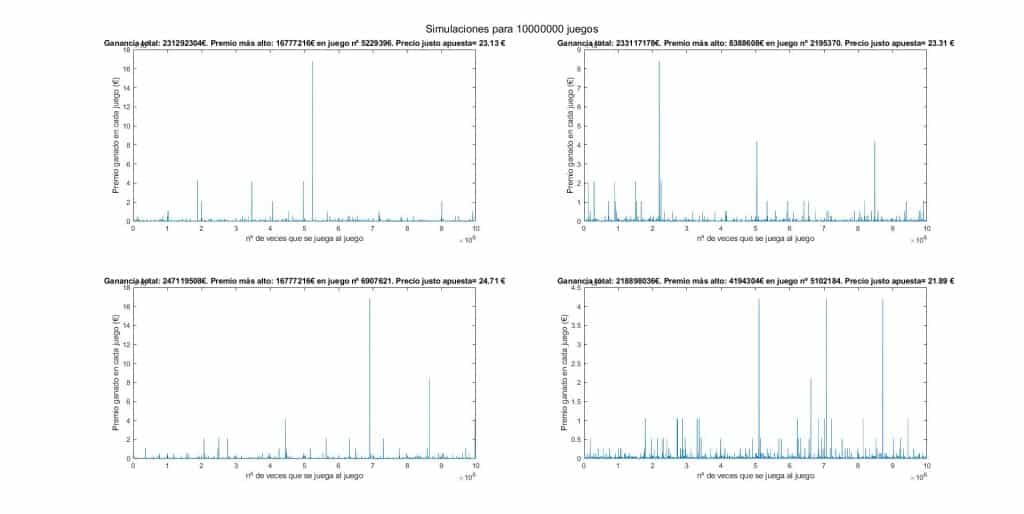
Se observa que, a medida que se realiza un mayor número de simulaciones, el precio justo de la apuesta tiende a equilibrarse ya que al final se compensan las simulaciones. Además, se ve que conforme aumenta el número de simulaciones también va aumentando ligeramente el precio justo de la apuesta. Esto se debe a que para que salga por ejemplo un premio asociado a una probabilidad del 10^-8% habrá que realizar un número de simulaciones del orden de 10^10.

Como el precio de la apuesta se va equilibrando constantemente, a mayor número de simulaciones más probable es que salga finalmente un premio gordo con un % de salir muy pequeño que incremente notablemente las ganancias y por lo tanto suba aún más el precio justo por apuesta.

Esto, en el caso de realizar un número de simulaciones elevadísimo (Mucho más del que puede soportar mi ordenador), nos llevaría a un incremento constante del precio justo por juego hasta llegar al infinito.

Recordad que el número máximo de simulaciones que he realizado es de 10^7, lo que estadísticamente corresponde a un premio máximo de sólo 10^7€ (De hecho se cumple en 2 de las 4 gráficas). Y eso nos da ya de por si un precio justo de 1€ por jugada. A eso hay que sumarle el resto de miniganancias que a su vez lo van incrementando. 1€ + 1€ + 1€…. De realizar 10^40 simulaciones no sólo se tenderá a ganar un premio de 10^40€ (+1€ precio justo) sino que además se obtendrán de media 10^33 premios de 10^7€ (10^40€), lo que a su vez nos dará otro euro al precio justo. Con un número infinito de juegos se tenderá por lo tanto a un precio justo de infinito, quedándose demostradas experimentalmente las matemáticas.

Juego limitado

También realicé una simulación del caso limitado. Limité el número máximo de fallos seguidos a 8 y por lo tanto según la esperanza matemática el precio justo de la jugada debería de ser de 8€. ¿Saldrá así?

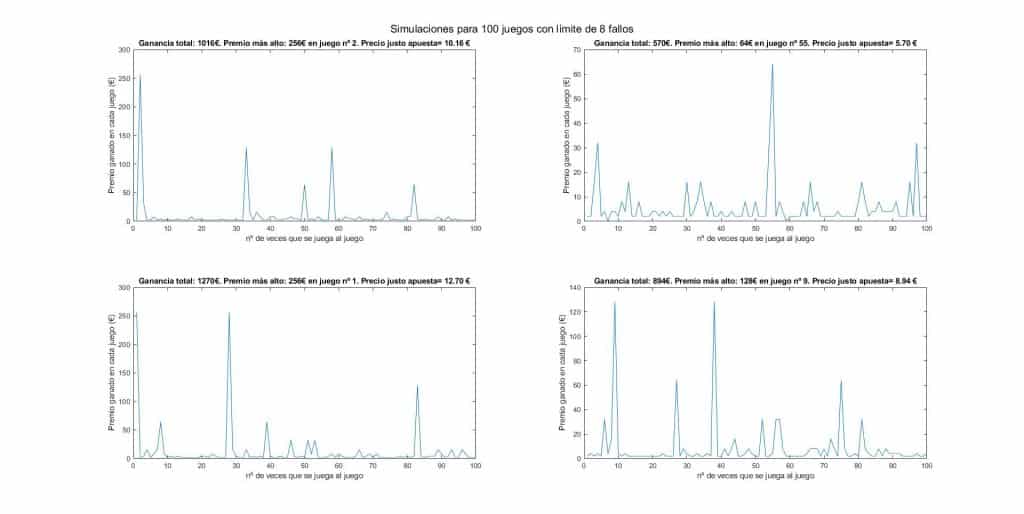
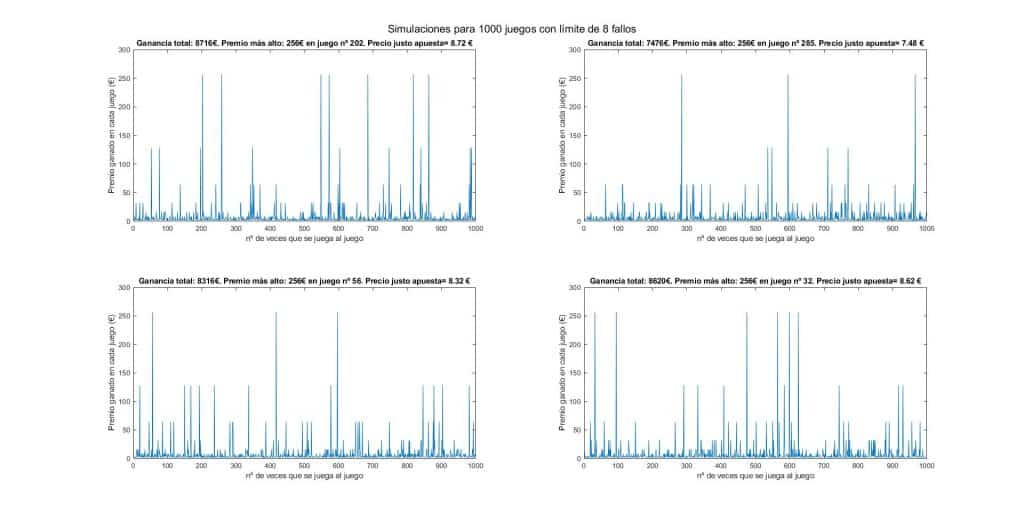
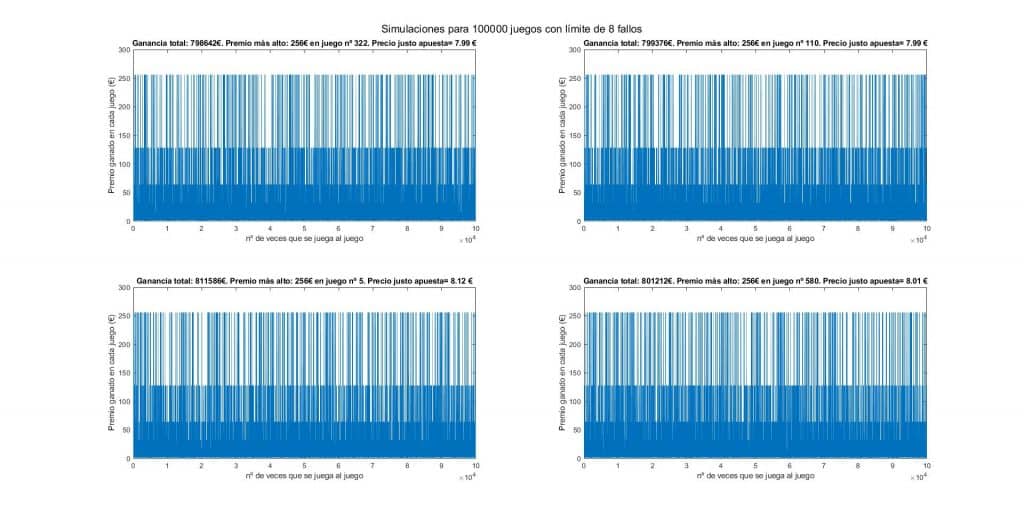
Efectivamente, se cumplen las matemáticas. Obviamente al aumentar el número de tiradas el valor se estabiliza y tiende a 8€.

Códigos de MATLAB

Estos son los códigos empleados para generar las gráficas. Para variar el número de simulaciones se cambia el valor de n y para variar el límite en el segundo caso es editando limite

Generación sin límite

n=10^3;

for c=1:4
suma=0;
valores=zeros(1,n);
n_tiradas=zeros(1,n);
for i=1:n

    flag=0;
    k=1;
while flag==0
    random=rand();
    if random<=0.5 %Sigue jugando
        k=k+1;
    else
        flag=1;
    end
end
        valores(i)=i;
        n_tiradas(i)=k;
end
premios=2.^n_tiradas;
[a,b]=max(premios);
ganancia_total=sum(premios');
precio_justo=ganancia_total/n;
precio_justo=round(precio_justo,2);

subplot(2,2,c)
str2=sprintf('Simulaciones para %d juegos',n);
sgtitle(str2)

plot(valores,premios);
xlabel('nº de veces que se juega al juego') 
ylabel('Premio ganado en cada juego (€)') 
str=sprintf('Ganancia total: %d€. Premio más alto: %d€ en juego nº %d. Precio justo apuesta= %.2f €',ganancia_total,a,b,precio_justo);
title(str)
end

Generación limitada

n=10^2;
limite=8;

for c=1:4
suma=0;
valores=zeros(1,n);
n_tiradas=zeros(1,n);
for i=1:n

    flag=0;
    k=1;
while flag==0
    random=rand();
    if random<=0.5 %Sigue jugando
        k=k+1;
        if k==limite+1
            k=0;
            flag=1;
        end
    else
        flag=1;
    end
end
        valores(i)=i;
        n_tiradas(i)=k;
end
premios=2.^n_tiradas;

for g=1:length(premios)
    if premios(g)==1
        premios(g)=0;
    end
end


[a,b]=max(premios);
ganancia_total=sum(premios');
precio_justo=ganancia_total/n;
precio_justo=round(precio_justo,2);



subplot(2,2,c)
str2=sprintf('Simulaciones para %d juegos con límite de 8 fallos',n);
sgtitle(str2)

plot(valores,premios);
xlabel('nº de veces que se juega al juego') 
ylabel('Premio ganado en cada juego (€)') 
str=sprintf('Ganancia total: %d€. Premio más alto: %d€ en juego nº %d. Precio justo apuesta= %.2f €',ganancia_total,a,b,precio_justo);
title(str)

end