La paradoja del cumpleaños

Tabla de contenidos

Introducción a la paradoja

¡Buenas! No hay ningún otro día más apropiado como este para hablar de cumpleaños, y por ello os presento la paradoja del cumpleaños.

Seguro que muchas veces os habéis preguntado qué probabilidad hay de que dos personas cumplan años. Eso se puede deber en parte a que siempre en el colegio había gente que cumplía años el mismo día.

Vamos a considerar que un año tiene 365 días. Eso son 365 posibles días (¡Son muchos días!) para cumplir años, agrupados entre los 12 meses del año.

Si yo os pregunto, ¿Cuál es el número mínimo de personas necesarias en un grupo para que la probabilidad de que dos personas cumplan años el mismo día sea mayor a de que nadie cumpla años el misma día?

Cualquier persona emplearía por intuición el siguiente razonamiento. Si hay 365 posibles días y la mitad es 182,5 , si en el grupo hay 183 personas la probabilidad de que dos personas cumplan años el mismo día es ligeramente superior al 50%.

Pero se equivocan. ¿Y si os dijera que en un grupo de 24 personas, la probabilidad de que 2 personas cumplan años el mismo día es del 54%?

El hecho de que sólo hagan falta 24 personas va contra nuestra intuición. Es por ello que se le llama la paradoja del cumpleaños.

Demostración matemática de la paradoja del cumpleaños

Para poder calcular la probabilidad de que en un grupo de N personas al menos 2 personas cumplan años el mismo día vamos a aplicar un razonamiento bastante intuitivo.

Partiremos de un concepto básico de Estadística el cual nos dice que la probabilidad de que un suceso ocurra es 1 menos la probabilidad de que no ocurra. Es decir, p= 1-q. Expresamos los porcentajes en tanto por 1. Es decir, que un p de 0,43 representa un 43%.

p = Probabilidad de que al menos 2 personas cumplan años el mismo día
q = Probabilidad de que ninguna persona cumpla años el mismo día

Y, en vez de calcular directamente la probabilidad p que es la que nos interesa, calcularemos q ya que es mucho más sencillo.

Supongamos que tenemos una fila «infinita» de personas y que preguntaremos la fecha de su cumpleaños a las N primeras personas, estimando la probabilidad de que llegado a la N persona no se haya repetido ninguna fecha.

El razonamiento es simple. La probabilidad de un suceso se calcula de esta forma:

\(Probabilidad=\frac{Sucesos \ favorables}{Sucesos \ posibles}\)

En nuestro caso la probabilidad de NO repetir día sería el número de días libres / números de días del año.

Además, al ir preguntando, la probabilidad de que no se repita un cumpleaños para la persona n implica que no se hayan repetido para las personas anteriores, por lo que habría que multiplicar por la probabilidad de la anterior. Así sucesivamente hasta llegar a la persona 1.

La probabilidad de sacar 1 rojo en la ruleta es aproximadamente del 50%. Pero la probabilidad de sacar 2 rojos seguidos es del 25%. Y la de sacar 3 rojos seguidos de 12,5%. ¿Claro?

Comenzamos estudiando el caso de 1 persona. En este caso la probabilidad de no repetir día es de \(\frac{365}{365}\), es decir 1. Al ser la primera fecha es imposible que se repita.
Con 2 personas. La probabilidad de NO repetir día es la probabilidad de no haber repetido día en la persona anterior y la de no repetir en esta, lo que se traduciría por \(\frac{365}{365} * \frac{364}{365}\)
Para 3 personas lo mismo. No haber repetido fecha al ir preguntando a cada una de las anteriores personas ni en esta última persona, es decir, \(\frac{365}{365} * \frac{364}{365} * \frac{363}{365}\)

…

Una vez encontrado el patrón de comportamiento vamos a realizar un poco de abstracción matemática. Para N personas sería la siguiente fórmula:

\(q(N)= \frac{365}{365} *\frac{364}{365}* \frac{363}{365}* \frac{362}{365} \cdots = \prod_{n=1}^{N-1} \frac{365-n}{365}\)

Observamos que, a medida que N crece, la probabilidad tiende a 0 rápidamente. Para el caso de que N=366 observamos fácilmente que la probabilidad de NO repetir fecha es 0. Es decir, es imposible porque en un caso IDEAL ha dado la casualidad de que las 365 personas a las que hemos preguntado anteriormente han cumplido años cada uno en un día distinto. Pero ya la persona nº 366 obligatoriamente debe repetir día (Considerando un año con 365 días)

\(\prod_{n=1}^{366-1} \frac{365-n}{365} = \frac{365}{365} *\frac{364}{365}* \frac{363}{365}* \frac{362}{365} \cdots \frac{2}{365} *\frac{1}{365}* \frac{0}{365} = 0\)

La probabilidad de que 2 personas coincidan sería p=1-q

Análisis funcional

Este productorio es cómodo si queremos calcular un valor para un N dado. Sin embargo, sería interesante realizar un análisis funcional a la paradoja del cumpleaños, ¿No?

Es por ello que, empleando factoriales, podemos introducir una función que estudie los valores de esta probabilidad

\( q=\left\{{\begin{array}{ll}{\frac {365!}{365^{n}(365-n)!}},&1\leq n\leq 365\\0,&n>365\end{array}}\right. \)

Lo que para la probabilidad p que queremos calcular de «Probabilidad de que dos personas cumplan el mismo día» se traduce en:

\( p=\left\{{\begin{array}{ll}1-{\frac {365!}{365^{n}(365-n)!}},&1\leq n\leq 365\\1,&n>365\end{array}}\right. \)

Link a gráfico en wolframalpha para valores de N=1 a 40

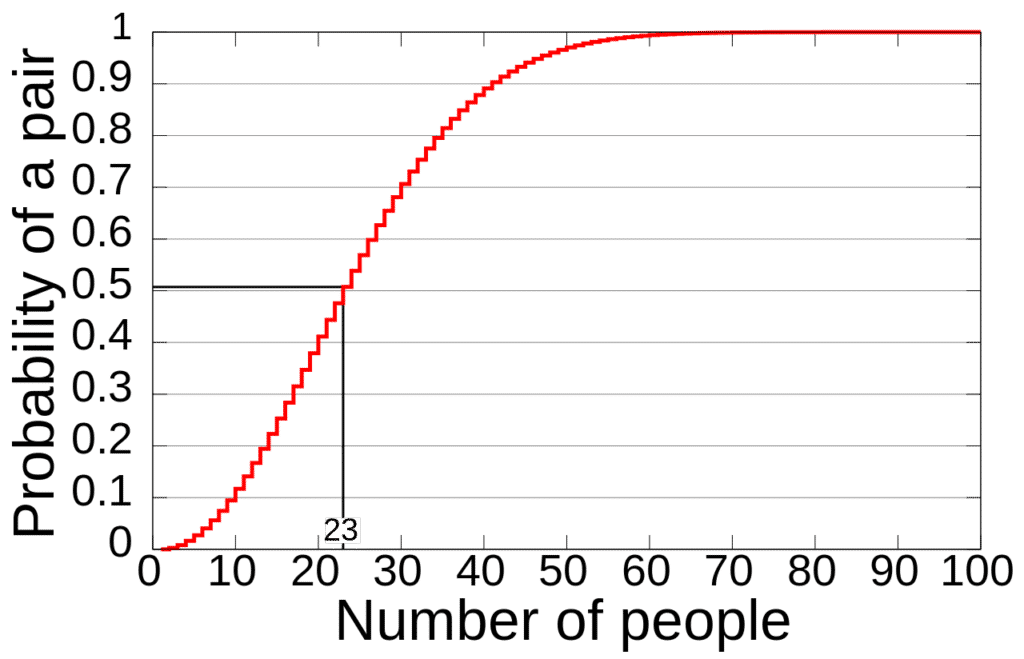
Gráfica probabilidad en la paradoja del cumpleaños

Dando resultados impresionantes como que con solo 50 personas la probabilidad es del 97%!!!

Jugadores de fútbol que cumplen años el mismo día

La paradoja del cumpleaños nos da resultados sorprendentes como de que, en cada partido de fútbol si contamos a los 11 jugadores de cada equipo, al árbitro y a los entrenadores (25 personas), ¡Hay una probabilidad del 57% de que dos personas cumplan años el mismo día!

Si no os lo creéis o simplemente queréis hacer pruebas sin abrir la wikipedia de todas y cada una de las personas y anotar sus cumpleaños haced lo siguiente: