La Ruleta. Toda la información. Métodos matemáticos para las apuestas

Todos conocemos La Ruleta, el famoso juego de casino en el que apuestas por una serie de números y, si la bola cae sobre una de tus apuestas, te llevas un beneficio proporcional al riesgo sufrido y lo apostado. Bueno, no es proporcional del todo…

Descubre en este artículo todos los datos acerca de la ruleta y técnicas que se emplean a la hora de apostar para «intentar» ganar a la casa. Ya de antemano aviso de que NO se puede ganar de ningún modo y no quiero promover dicho juego por ese mismo motivo. No obstante, los métodos están ahí y unos son mejores que otros…

La versión de la ruleta que conocemos hoy en día es una variación del juego que ideó el matemático Blaise Pascal en el siglo XVII. Originalmente la ruleta tenía 36 números, ordenados meticulosamente y separados entre sí de tal forma que no existen zonas en las cuales cierta apuesta tenga mayor probabilidad (A menos de apostar números seguidos en concreto).

Debido a la gran popularidad del juego (No nos engañemos, es muy emocionante ver cómo la bola va saltando y saltando mientras miramos nuestro número…) , las empresas vieron en ella un negocio. Sin embargo, al ser estadísticamente equilibrada, a la larga el dinero que se apostaba acababa saliendo por igual (Probabilidad de 1/36 de acertar un número, ganando x36 lo apostado). Por ello, en 1842 los hermanos Blanc modificaron la ruleta añadiendo el número 0.

De esta forma la probabilidad de acertar lo apostado es de 1/37 mientras que se mantiene la ganancia x36, quedando un margen de 2,073% de beneficio para la casa (Ese 1/37 de caer en el 0)

No contentos con el beneficio, en algunos países se ideó una nueva versión en la que se añadía otro cero más (00), quedando el beneficio en 5,263% (2/38)

Tipos de ruleta

Ruleta Francesa

Es la empleada a nivel europeo y en muchas casas de apuesta online. Consta de 37 números de los cuales uno de ellos es el 0 verde, de forma que si en una ronda la bola cae en dicha casilla se perderán todas las apuestas. Ahí la casa gana su 2,073% de beneficio

Ruleta Americana

Es una variación de la francesa mucho más egoísta, siendo en este caso 38 el número de casillas, entre las cuales destaca el 0 y el 00. En caso de caer en cualquiera de dichas casillas la casa se lleva el dinero de las apuestas, siendo el beneficio aún mayor (5,263%) y no habiendo ventajas respecto a la francesa.

Conclusiones

Hay que elegir siempre la ruleta francesa por motivos obvios. Existen diferencias entre ambas además de la presencia del 00 como puede ser la forma de juego (Mayor velocidad en la americana), el tamaño del tapete o la disposición de los números.

Se supone que además en la ruleta francesa existe la regla «En prisión«, la cuál dictamina que si en una apuesta sencilla la bola cae en el 0, no se pierde la apuesta sino que se guarda para la siguiente ronda o se recupera la mitad de lo apostado en caso de arrepentimiento. No obstante, lo normal es que la casa omita esta regla… Pero es algo que debe tenerse en cuenta.

Tipos de apuestas

Apuestas sencillas

Se apuesta a un conjunto de números, siendo la probabilidad de acertar de 18/37 y obteniendo x2 de ganancia en caso de ganar.

Los números están distribuidos de manera que ningún número que contenga a un(os) conjunto(s) se encontrará justo al lado de otro del mismo.

En total hay 18 números rojos, de los cuales 9 son impares y 9 pares. Y de los cuales 9 son menores o igual a 18 (1 al 18) y 9 son mayores que 18 (19-36) . Lo mismo ocurre para los otros 18 negros. De esta forma se equilibra totalmente las apuestas y se hace la distribución de cada uno de los números única.

Rojo o Negro

Cada número tiene un color asignado. Es la apuesta más evidente y popular.

Par o Impar

Se apuesta a números pares o impares. El 0, a pesar de ser par, no se tiene en cuenta

Falta o Pasa

Falta si el número es (1-18) y Pasa si el número es (19-36)

Apuestas múltiples

Se apuesta el dinero a uno o varios números que se encuentran separados en la ruleta.

Apuestas a un número (Pleno)

Se apuesta todo a uno de los 37 números. Se paga x36 de lo apostado.

Apuestas a una pareja o caballo

Se apuestan a dos números a la vez, obteniendo x18 de ganancia.

Cuadro

Se apuestan a cuatro números a la vez, obteniendo x8 de ganancia.

Columnas

Se a puesta a una de las columnas (12 números). Se obtiene x3 de ganancia.

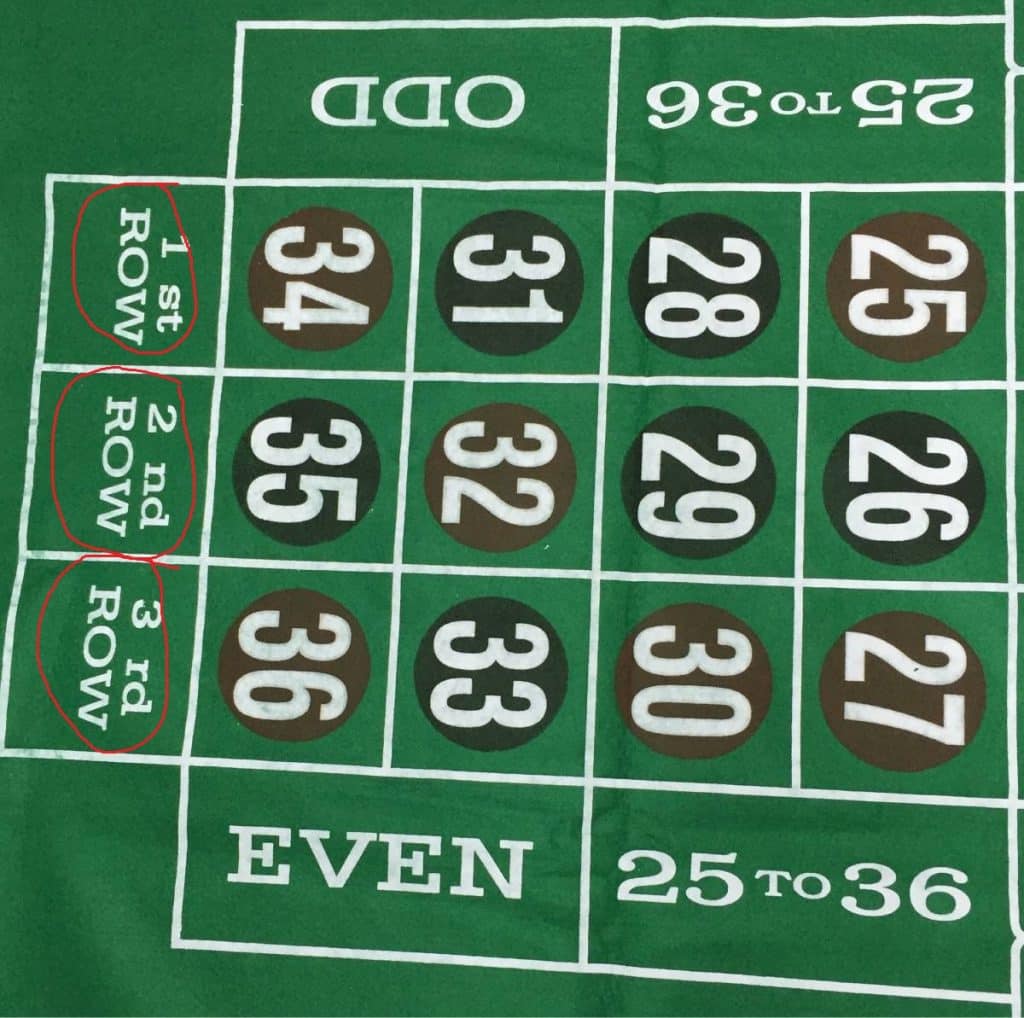
Docenas

Se apuesta a una de las docenas (1-12,13-24,25-36). Se obtiene x3 de ganancia.

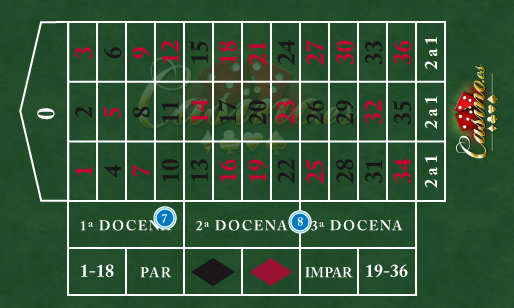
Apuestas clásicas por sectores

En este tipo de apuestas se juegan por sectores de la ruleta. Los números a los que se juegan se encuentran agrupados en una zona en concreto de la ruleta.

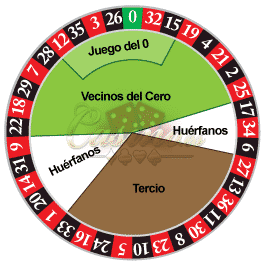
Juego del 0

Se juegan 6 números (Sin incluir el 0), obteniendo x6 de ganancia.

Vecinos del 0

Se juegan 16 números (Sin incluir el 0), con x2,25 de ganancia

Huérfanos

Se juegan 8 números (Sin incluir el 0), obteniendo x4,5 de ganancia.

Tercio

Se juegan 12 números, obteniendo x3 de ganancia.

Conclusiones

Hay muchos tipos de apuesta y cada uno tiene sus preferidos. Hay que destacar que el riesgo/ganancia es el mismo en todas las apuestas. El beneficio es inversamente proporcional a la probabilidad de acertar.

Ej: Apuesto a una combinación en la cuál se juegan 8 números por igual –> Prob: 8/36 –> Ganancia: 36/8 = x4,5 sobre lo apostado

Métodos matemáticos

Desde que se popularizó su uso se han ideado métodos de apuestas mediante algoritmos que intentan maximizar el beneficio / reducir el riesgo de pérdida jugando con la probabilidad y variando la cantidad de la apuesta en función de cómo van saliendo las apuestas. Os presento los métodos más conocidos.

La Martingala

La conocidísima, archiconocida, archiconocidísima, la más popular… La Martingala. Empleada por todo el mundo que mínimamente haya intentando ganarle a la casa siguiendo un algoritmo de apuestas en lugar de apostar a lo loco.

Ya lo adelantamos al principio: No existe ninguna técnica que funcione para ganar a la larga. A pesar de ello, La Martingala es el sistema de apuestas más popular debido a su sencillez y que teóricamente ganarías siempre a la ruleta.

El Algoritmo

En primer lugar debemos de definir nuestra apuesta inicial, a la que llamaremos x, y decidir a qué vamos a apostar. Debemos de elegir una apuesta sencilla (Rojo-Negro, Par-Impar, Pasa-Falta) para asegurarnos de que la ganancia es x2 en todo momento y el riesgo es de 1/2

El método consiste en:

• Apostamos la apuesta inicial si ganamos la ronda
• Multiplicamos la apuesta anterior x2 en caso de pérdida durante cada una de las tiradas de nuestra ronda hasta que ganemos la ronda.

No hay más. Pongo un ejemplo apostando al rojo con x=1€. Una ronda se considera un conjunto de tiradas antes de que ganemos, quedando cerrada la ronda.

• Ronda 1: Apostamos 1€ (-1€) ganamos –> +1€ de beneficio
• Ronda 2: Apostamos 1€ (-1€) perdemos –> Apostamos 2€ (-3€) perdemos –> Apostamos 4€ (-7€) ganamos —> Obtenemos 8€ –> +1€ de beneficio
• Ronda 3: Apostamos 1€ (-1€) perdemos –> Apostamos 2€ (-3€) ganamos –> Obtenemos 4€ –> +1€ de beneficio
• ……
• Ronda 50: Apostamos 1€ (-1€) perdemos –> Apostamos 2€ (-3€) perdemos –> Apostamos 4€ (-7€) perdemos —> Apostamos 8€ (-15€) perdemos–> Apostamos 16€ (-31€) perdemos –> Apostamos 32€ (-63€) ganamos —> Obtenemos 64€ –> +1€ de beneficio
• ….
• Ronda n: ……. Apostamos \(2^{k}\)€ \((-[2^{k+1}-1])\)€ ganamos–> Obtenemos \(2^{k+1}\)€ –>+1€ de beneficio
• …
• Ronda m: …… Apostamos \((2^{k}*x)\)€ \((-[(2^{k+1}*x)-x])\)€ ganamos–> Obtenemos \((2^{k+1}*x)\)€ –>+\(x\)€ de beneficio

Siendo k el número de tiradas perdidas durante la ronda y x el valor de la apuesta inicial. Observamos que en cada ronda una vez que ganamos obtenemos como beneficio la cantidad inicial apostada

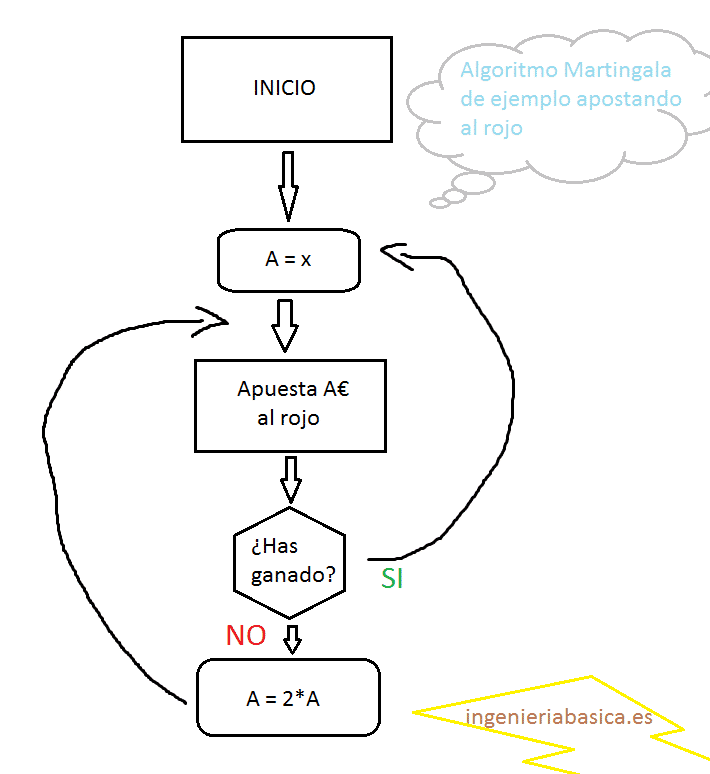
¿Es perfecto?

En un mundo ideal en el que tuvieramos dinero infinito y no hubiera apuesta máxima SÍ. No obstante, el dinero no es infinito y todos los casinos tienen limitada la apuesta máxima. Por lo tanto, si bien jugando un par de rondas se puede ganar algo, en cuanto haya varios fallos seguidos la cantidad que debemos apostar crecerá exponencialmente, haciendo inviable la apuesta y perdiéndolo todo.

Muchos que estén leyendo esto se están frotando las manos y van a intentar una apuesta inicial de 1€ teniendo como dinero disponible 50€ por ejemplo. El número de fallos seguidos que pueden soportarse son 4, ya que no podremos tirar una 5ª oportunidad al estar sin fondos. Sí, las matemáticas vuelven a superar a la intuición ya que estamos subestimando el incremento exponencial. ¿ Y si empezamos con 100€? Soportaremos sólo 5 fallos, a pesar de tener disponible el doble de dinero que antes.

Creedme, he hecho pruebas con simuladores poniendo como saldo inicial billones de euros y he llegado a perder 30 veces seguidas (¡Es posible!), lo que supone una pérdida de 2.147.483.647€ (Billones de euros!). Haced vuestras pruebas aquí, tenéis todo el dinero del mundo (Que nunca es infinito):

https://www.bettingsimulation.com/

Sistema Fibonacci

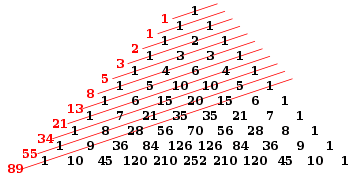
Es similar a la Martingala pero siguiendo la serie de Fibonacci: 1,1,2,3,5,8,13,21…n

El Algoritmo

Siendo \(n_{k}=n_{k-1}+n_{k-2}\) para \(k\geq 3\), con \(n_{1}=n_{2}=1\), y \(n_{0}=0\)

Cada vez que ganamos apostamos 1€. Y cuando perdamos apostamos el número inmediatamente posterior al jugado según la serie de fibonacci.

La apuesta en el caso de pérdida es \(n_{k+1}\), siendo lo perdido en ese momento un total de \(n_{k+3}-1\), y siendo k el número de veces perdidas previamente en el momento de apostar. En caso de ganancia obtendríamos \(2*n_{k+1}\).

Si desarrollamos, dado un número de apuestas perdidas k, en caso de ganar:

• Apostamos \(n_{k+1}\)
• Ganamos \(n_{k+1}+n_{k+1}\)
• Nuestra pérdida acumulada es \(n_{k+3}-1=(n_{k+2}+n_{k+1})-1=((n_{k+1}+n_{k})+n_{k+1})-1\)
• Nuestro saldo neto es: Ganancia – Pérdida acumulada= \(1-n_{k}\)

Quedando patente en el último punto que con un k mayor de 2 estaríamos perdiendo dinero.

Observamos que al cerrar la ronda (Ganar):

• Si no hemos perdido ninguna -> Obtenemos 1€ en dicha ronda
• Si hemos perdido 1 -> Nos quedamos como estábamos antes de tirar
• Si hemos perdido 2 -> Nos quedamos como estábamos antes de tirar
• Si hemos perdido 3 -> Estamos con nuestro saldo – 1€
• Si hemos perdido 4 -> Estamos con nuestro saldo – 2€
• ….
• Si hemos perdido 7 -> Estamos con nuestro saldo – 12€

¿Qué tiene de especial?

Es un sistema conservador, el cual se podría usar en caso de disponer de poco dinero ya que las apuestas no crecen exponencialmente y pueden controlarse o al menos se puede seguir jugando.

Por ejemplo, llevando perdidas 7 rondas tendríamos que apostar según Fibonacci 21€; mientras que según la Martingala tendríamos que apostar 255€.

Sin embargo, el inconveniente es evidente. En la Martingala SIEMPRE ganamos a menos que nos quedemos sin dinero. En Fibonacci únicamente ganamos dinero si finalizamos la ronda sin haber perdido nunca. Nos permiten hasta 2 pérdidas (Es decir, tirar una 3º vez de la ruleta y ganarla) para finalizar la ronda sin perder ni ganar nada.

Si en una ronda llevamos 3 perdidas, lo siguiente va a ser perder tanto dinero como tiradas vayamos fallando a pesar de que ganemos finalmente.

Fibonacci vs Martingala

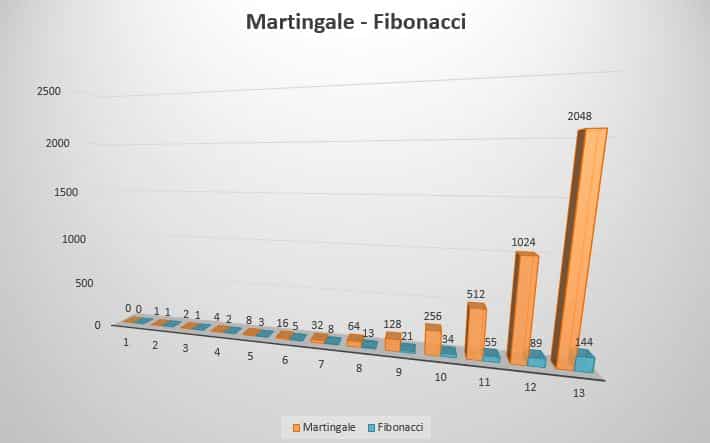
Tras hacer un par de pruebas he comprobado que para 10.000 tiradas:

Disponiendo de poco dinero (2.000€)

• Con la Martingala nos quedamos en 0€ alrededor de la ronda 3000.
• Con Fibonacci solemos ganar algunos casos, siendo la ganancia estimada en 1500€.

Disponiendo de mucho dinero (20.000€)

• La Martingala llega a ganar en más pruebas, siendo la ganancia del orden de 5000€. Cuanto mayor es nuestro dinero, menor es el número de pérdidas y mayor nuestra ganancia.
• Fibonacci sigue un ritmo similar al caso de poco dinero, siendo la ganancia de 1500€ en general.

Conclusiones

Se acaba perdiendo dinero en ambas… No obstante hay veces en las que se gana dinero. Y en general se extrae que si bien se pierde a la larga, cuanto mayor dinero tenemos menos probabilidades tenemos de perder empleando la Martingala. Sin embargo, a Fibonacci no le afecta la cantidad que tengamos.

Faltaría un estudio variando y combinando nº de tiradas y saldo disponible, os lo dejo a vosotros:

https://www.bettingsimulation.com/

Estrategia de D’Alembert

El célebre matemático del siglo de las luces D’Alembert, el mismo de la Paradoja de D’Alembert, también ideó un método para la ruleta.

Consiste en:

• Elegimos una cantidad inicial para apostar
• Si ganamos -> Reducimos en 1€ nuestra cantidad inicial y la apostamos
• Si perdemos -> Aumentamos en 1€ nuestra cantidad inicial y la apostamos

Me parece muy interesante ya que fijamos una cantidad la cual nos puede servir para indicarnos cuando salir del juego, cosa esencial para evitar la bancarrota porque cuanto más tiempo pasemos más probabilidades tenemos de perderlo todo.

Ejemplo

Pongamos un ejemplo comenzando con 5€:

Apostamos 5€ (-5€) y perdemos

Apostamos 6€ (-11€) y perdemos

Apostamos 7€(-18€) y ganamos –> Estamos en (-4€)

Apostamos 6€ (-10€) y perdemos

Apostamos 7€ (-17€) y ganamos –> Estamos en (-3€)

Apostamos 6€ (-9€) y ganamos –> Estamos en (+3€)

…..

Se observa que se gana dinero sólo si se gana el mismo número de veces que de derrotas (Y, obviamente si tenemos mas victorias que derrotas), de tal forma que para cuando lleguemos al número inicial tendremos tantos € de beneficio como victorias/derrotas hayamos tenido. Es decir, el número de tiradas totales/2.

Además, el beneficio es independiente de nuestra apuesta inicial, lo cual indica que lo mejor es hacer una apuesta inicial baja. Sin embargo, limitamos nuestras ganancias en positivo ya que si tenemos más victorias que derrotas y no podemos seguir disminuyendo el numero de apuestas deberíamos de comenzar desde 0.

Conclusiones

Puede ser un método para jugar un par de minutos y ganar unos euros. La principal ventaja es que si tenemos la misma proporción de victorias/derrotas ganamos dinero. Y si tenemos más victorias que derrotas ganamos aún más.

No obstante, al ser la probabilidad de ganar inferior al 50% (48,65%) a la larga tendríamos más derrotas que victorias, por lo que perderemos dinero.

Estrategia de Labouchere

Llegando casi al final del artículo os presento la estrategia más compleja: La Estrategia de Labouchere.

Es similar a la estrategia D’Alembert ya que se va sumando o restando en caso de pérdida o ganancia respectivamente.

El método

Al igual que en D’Alembert, se parte de una apuesta inicial, la cual será nuestro objetivo de ganancia. Digamos que queremos ganar 9€. Primeramente deberemos de repartir esa cantidad en números pequeños formando una serie (De 5-6 dígitos) de menor a mayor tipo: 1-1-2-2-3

El método consiste en:

• Sumamos el primer y último dígito de la serie y lo apostamos.
• Si ganamos-> Tachamos dichos dígitos y repetimos con lo siguientes dígitos.
• Si perdemos añadimos la apuesta realizada (Suma de los dígitos) al final de la serie y repetimos.

Así hasta que nos quedemos sin números en la serie, que ocurrirá cuando obtengamos el mismo número de victorias que derrotas. Si tenemos más victorias que derrotas la finalizaremos antes.

El beneficio al completar la serie será la suma total que establecimos al principio. Pongamos un ejemplo con los 9€:

1-1-2-2-3

Apostamos (1+3) 4€ –> Perdemos –> 1-1-2-2-3-4

Apostamos (1+4) 5€ –> Ganamos –> 1-2-2-3 [Observamos que nos hemos quitad un dígito respecto al principio]

Apostamos (1+3) 4€ –> Ganamos –> 2-2

Apostamos (2+2) 4€ –> Perdemos –> 2-2-4

Apostamos (2+4) 6€ –> Ganamos –> 2

Apostamos 2€ –> Perdemos –> 0-2-2

Apostamos 2€ –> Perdemos –> 2-2-2

Apostamos (2+2) 4€ –> Ganamos –> 2

…. Llegados a este punto tenemos un beneficio de 7€. Podemos seguir en bucle hasta que ganemos una victoria más de la cuenta y lo finalicemos.

Conclusiones

La principal ventaja de emplear este método es que podemos marcarnos una ganancia límite y de hecho vamos jugando siempre con esa ganancia en mente. Por ello, al igual que con D’Alembert, puede aplicarse para una ganancia pequeña en un par de minutos y así conseguir unos euros. Además, no crece exponencialmente por lo que lo podemos controlar. Del mismo modo, en caso de tener una serie con números grandes debido a un gran número de derrotas, podemos reagruparla en otra serie. Por ejemplo:

3-5-11 es equivalente a 1-2-2-4-4-6. De manera que podemos seguir apostando en caso de no tener suficiente saldo para completar la apuesta.

Conclusión final y cálculo de probabilidades

Probabilidades

Os dejo por aquí una serie de fórmulas para calcular las probabilidades de las apuestas.

• La probabilidad de acertar una apuesta es \(\frac{x}{37}\), siendo x el número de números involucrados en la apuesta. Llamémosla p. Para poder expresarlo en %, hacemos 100*p
• La probabilidad de ganar n veces seguidas una apuesta es de \(p^{n}\)
• La probabilidad de fallar n veces seguidas una apuesta es de \((1-p)^{n}\)

Apostando a una apuesta sencilla, con p= 18/37, la probabilidad de fallar 7 veces seguidas es de \((\frac{19}{37})^{7}= 0.0094 \), es decir, un 0,94%. Lo que indica que de cada 100 rondas que hagamos por ejemplo de la martingala, en 1 de ellas tendremos 7 pérdidas seguidas, lo que implicaría tener un negativo de 127€

Conclusión final

Lo vuelvo a repetir: No se puede ganar a la ruleta a la larga. Si queréis hacer experimentos usad webs online para ello y sacad conclusiones.

La única forma en la que se puede ganar a la ruleta es a corto plazo. Y ello se debe a que, a diferencia de la ruleta, nosotros nos podemos ir cuando queramos.

¿Cómo podemos aprovecharnos de esto?

Hay apuestas más o menos volátiles. Las de mayor volatilidad presentan menor % de ganar pero, en caso de hacerlo, el premio es elevado (Apuestas a un número por ejemplo). Las de menor volatilidad son más lentas pero con menos riesgo (Apuesta de rojo-negro).

Lo que tienen las apuestas menos volátiles es que requieren de tiempo para ir obteniendo beneficios a la larga. Sin embargo, al estar jugando con desventaja al tener el 0, a la larga es como perdemos precisamente.

La única posibilidad de poder ganar algo es apostar a 1-4 números hasta ganar e irnos. O hacer una única serie de Labouchere e irnos. De este modo, si hemos tenido suerte y hemos podido ganar antes de estar en pérdidas podemos irnos con un par de € ya que al no jugar a la larga y no equilibrarse los % de victorias y derrotas estamos evitando el efecto del 0 y si tenemos suerte podemos evitar el implacable e inevitable efecto de las matemáticas. El inconveniente es que puede que por ejemplo llevemos 37 tiradas y no hayamos aún acertado nuestro número. En este caso estaríamos en pérdidas completamente. No se puede asegurar nada y por ello no recomiendo jugar a la ruleta con dinero real.