Demostración de las fórmulas de área y volumen mediante integrales

¡Buenas! En esta entrada se demostrará matemáticamente las fórmulas que todos conocemos de área y volumen de cuerpos conocidos como cubos, círculos, esferas, pirámides…

Para ello, cómo no, emplearemos la integral, una herramienta matemática esencial para cualquier tipo de cálculo que incluya una suma infinitesimal de diferentes valores.

Para poder comprender a la perfección determinados cálculos expuestos hay que saber como mínimo integrar en una variable, y es muy recomendable visitar este artículo: Integrales dobles y triples. Cambios de variables

Las fórmulas

Para calcular un área o volumen, lo que se hace es calcular la integral (Simple, doble, triple, curvilínea, de superficie…) de la función constante f=1 sobre el recinto cuyas dimensiones queremos calcular.

Paralelepípedo

Emplear integrales para este cuerpo geométrico es equivalente a matar moscas a cañonazos; no obstante, como primera utilidad básica de las integrales dobles y triples vamos a calcular su volumen

Volumen

Nuestro recinto de integración es un paralelepípedo de lados \(a\), \(b\) y \(c\). Por lo tanto, el volumen consiste en integrar \(1\) en un recinto definido por dichas dimensiones:

\(\displaystyle \int_{0}^{c} \int_{0}^{b} \int_{0}^{a} \ dxdydz = \int_{0}^{c} \int_{0}^{b} a \ dydz = \int_{0}^{c} a \cdot b \ dz = a \cdot b \cdot c\)

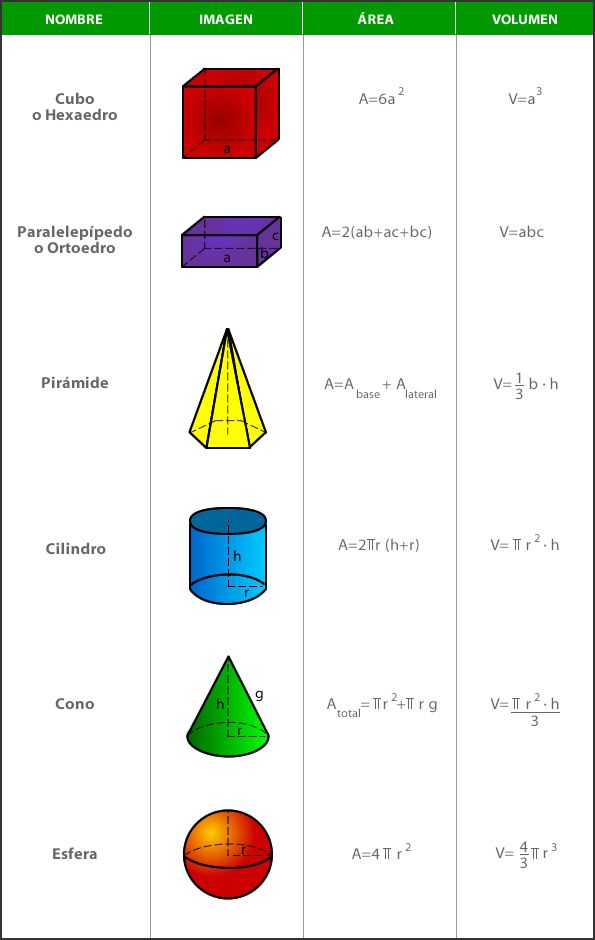
Círculo

Todo el mundo conoce sus fórmulas: \(2\pi r\) y \(\pi r^{2}\). Pero, ¿Cómo se deducen?

Antes que nada, hay que saber que si queremos representar gráficamente una función con forma de circunferencia no se puede representar tan fácilmente de la forma y=f(x) ya que no es inyectiva, es decir, para un valor de x aparecen 2 valores de y (La fórmula general para un radio r y centrado en el origen de coordenadas es \(x^{2} + y^{2} = r^{2}\). (En el caso de querer pintar un círculo, basta con cambiar = por <=). Por ello se emplea la parametrización:

\(x = r \cdot cos(\theta)\)

\(y= r \cdot sin(\theta)\)

Con \(r \in [0,R] \) y \(\theta \in [0,2\pi]\)

Cuyo determinante jacobiano, para el cambio de variables es: \(r\)

Si quieres saber más de la circunferencia y cómo se obtiene su fórmula de una manera más detallada, este es tu artículo

Aquí puedes jugar un poco con la ecuación de la circunferencia: Enlace a Desmos

Perímetro

El recinto es ese «alambre» que conforma el borde externo del círculo. Por lo tanto, la curva parametrizada de dicho alambre es:

\(C(\theta) = (R \cdot cos(\theta), R \cdot sin(\theta))\)

Y su derivada con respecto al ángulo recorrido resulta:

\(C'(\theta) = (-R \cdot sin(\theta), R \cdot cos(\theta))\), con \(||C'(\theta)|| = 1\)

La integral curvilínea sobre una función se define como:

\(\displaystyle \int_{C} f(s) \ ds := \int_{0}^{2 \pi} f(C(\theta)) \cdot ||C'(\theta)|| \ d\theta\)

Sustituyendo nuestros valores sabiendo que nuestra función a integrar es \(f=1\):

\(\displaystyle \int_{0}^{2 \pi} R\ d\theta = 2 \pi R\)

Una alternativa más intuitiva es pensar que si la longitud de un tramo \(ds\) de una circunferencia es igual a el radio por el ángulo \(d\theta\) recorrido, el perímetro (es decir, la longitud total) es igual a una suma infinitesimal de todos los tramos recorriendo la circunferencia de \(0\) a \(2\pi\):

\(\displaystyle \int_{0}^{2\pi} R \ d\theta = 2 \pi R\)

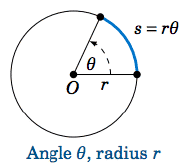
Área

Para calcular el área basta con calcular la integral sobre el recinto delimitado por la circunferencia. Para facilitar los cálculos pasamos de coordenadas cartesianas \((x,y)\) a polares \((r,\theta)\) empleando el jacobiano \(r\) para el cambio de variable. El recinto será delimitado por el radio \(r \in [0,R]\) y recorrido por el ángulo \(\theta \in [0,2\pi]\)

\(\displaystyle \iint_{S} \ dxdy= \int_{0}^{2\pi} \int_{0}^{R} r \ dr d\theta= \int_{0}^{2\pi} \dfrac{R^{2}}{2} d\theta = \pi R^{2}\)

Del mismo modo, una alternativa intuitiva es pensar que si tomamos un sector muy pequeño de una circunferencia, podemos aproximar dicho sector como si fuese un triángulo rectángulo, de forma que el área de un pequeño triángulo de altura \(ds=R \cdot d\theta\) resultado de recorrer un \(d\theta\) es \(\dfrac{R \cdot ds}{2} = \dfrac{R^{2}}{2} d\theta\)

Si sumamos el área de todos los triángulos recorriendo toda la circunferencia podemos obtener el área del círculo:

\(\displaystyle \int_{0}^{2\pi}\dfrac{R^{2}}{2} \ d\theta = \pi R^{2}\)

Esfera

En el caso de las esfera sus fórmulas son algo más desconocidas. \(\dfrac{4}{3} \cdot \pi \cdot r^{3}\) para el volumen y \(4 \cdot \pi \cdot r^{2}\) para el área de su superficie.

Al igual que con el círculo, emplearemos otras coordenadas, las coordenadas esféricas. La ecuación de la esfera en cartesianas es \(x^{2}+y^{2}+z^{2}\leq R\).

La parametrización es:

\(x = r \cdot sin(\theta) \cdot cos(\phi)\)

\(y = r \cdot sin(\theta) \cdot sin(\phi)\)

\(z = r \cdot cos(\theta)\)

Con \(r \in [0,R]\) , \(\phi \in [0,2\pi]\) y \(\theta \in [0,\pi]\)

Cuyo jacobiano es \(r^{2} \cdot sin(\theta)\)

Aquí puedes jugar un poco con la ecuación de la esfera: Entra a Geogebra 3D y pega esto en el editor: Superficie(r*sen(u)*cos(v),r*sen(u)*sen(v),r*cos(u),u,0,pi,v,0,2pi)

Área

Para calcular el área, basta con calcular la integral sobre el recinto recorrido por la parametrización con el radio fijo, es decir, \(r=R\). Calculamos la integral haciendo el cambio de variable con el jacobiano.

\(\displaystyle \iint_{S} \ dxdy= \int_{0}^{\pi} \int_{0}^{2\pi} R^{2} \cdot sin(\theta) \ d\phi d\theta= 2 \cdot \pi \cdot R^{2} \int_{0}^{\pi} sin(\theta) \ d\theta = 4 \cdot \pi \cdot R^{2}\)

Volumen

Para el volumen calculamos la integral de todo el recinto \(dxdydz\) empleando las variables \(drd\theta d\phi\)

\(\displaystyle \iiint_{V} dxdydz= \int_{0}^{\pi} \int_{0}^{R} \int_{0}^{2\pi} r^{2} \cdot sin(\theta) \ d\phi dr d\theta= 2 \cdot \pi \int_{0}^{\pi} \int_{0}^{R} r^{2}\cdot sin (\theta) \ dr d\theta =\)

\(\displaystyle = 2 \cdot \pi \cdot \dfrac{R^{3}}{3} \int_{0}^{\pi} sin(\theta) \ d\theta=\dfrac{4}{3} \cdot \pi \cdot R^{3} \)

Pirámide

La forma de calcular el volumen de una pirámide de base cuadrada \(b\) y altura \(h\) es idéntica a la de un paralelepípedo; la complicación es establecer los límites de integración (el recinto).

Tirando de lógica, la coordenada \(z\) va a ser libre, variando desde 0 a h. Las coordenadas \(x\) e \(y\) van a depender de la coordenada \(z\) en cuanto a los máximos valores que toman, partiendo desde -b/2 a b/2 como máximo en la base y tomando como valor único 0 cuando la \(z=h\) (pico de la pirámide). Basándonos en este planteamiento, tomamos los límites de las variables:

\(– \dfrac{b}{2} \cdot (1-\dfrac{z}{h}) \leq x \leq \dfrac{b}{2} \cdot(1-\dfrac{z}{h})\)

\( – \dfrac{b}{2}\cdot(1-\dfrac{z}{h}) \leq y \leq \dfrac{b}{2} \cdot(1-\dfrac{z}{h}) \)

\(0 \leq z \leq h\)

Volumen

Calculamos la integral sobre el recinto delimitado por \(dxdydz\):

\(\displaystyle V=\iiint_{V}dxdydz=\int_{0}^{h} \int_{ – \frac{b}{2}\cdot(1-\frac{z}{h}) }^{ \frac{b}{2} \cdot(1-\frac{z}{h}) } \int_{ – \frac{b}{2}\cdot(1-\frac{z}{h}) }^{ \frac{b}{2} \cdot (1-\frac{z}{h}) } \ dx dy dz= \)

\(\displaystyle = \int_{0}^{h} b^{2}\cdot(1-\frac{z}{h})^{2} \ dz = b^{2} \int_{0}^{h} (1+\frac{z^{2}}{h^{2}}-\frac{2z}{h}) \ dz = \dfrac{1}{3} b^{2} \cdot h\)

Cono

El cono es muy similar a la pirámide. No obstante, debemos de emplear coordenadas polares para poder parametrizar correctamente la base circular. Emplearemos las variables \( \ z, \ r \ y \ \theta \). Siguiendo una deducción similar a la pirámide nos queda:

\(0 \leq z \leq h\)

\(0 \leq r \leq R \cdot (1-\frac{z}{h})\)

\( 0 \leq \theta \leq 2\pi\)

Volumen

Calculamos la integral sobre el recinto delimitado por \(dxdydz\) y hacemos el cambio de variable a polares con jacobiano \(r\)

\(\displaystyle V=\iiint_{V}dxdydz=\int_{0}^{h}\int_{0}^{ R \cdot (1-\frac{z}{h}) }\int_{0}^{2\pi} r \ d\theta dr dz=2\pi \int_{0}^{h}\int_{0}^{ R \cdot (1-\frac{z}{h})} r \ dr dz =\)

\(\displaystyle = \pi \int_{0}^{h} R^{2} \cdot (1-\dfrac{z}{h})^{2} \ dz = \pi R^{2} \int_{0}^{h} (1 + \dfrac{z^{2}}{h^{2}} – \frac{2z}{h}) \ dz = \dfrac{1}{3} \pi \cdot R^{2} \cdot h\)

Que, como anticipábamos, al igual que la pirámide, su fórmula de volumen es:

\(\dfrac{1}{3} \cdot Area \ de \ la \ base \cdot Altura\)

Cilindro

El cilindro es quizás la figura más intuitiva a la hora de calcular el área de la superficie y su volumen. A pesar de ser obvio, vamos a mostrar cómo se podría calcular su volumen de forma integral (Siendo, claramente, área de la base * altura) para que se comprenda mejor el funcionamiento de integrales triples.

Emplearemos las variables \(\ z, \ r \ y \ \theta\) tal que:

\(0 \leq z \leq h\)

\( 0 \leq r \leq R\)

\(0 \leq \theta \leq 2\pi\)

Volumen

Calculamos la integral sobre el recinto delimitado por \(dxdydz\) y hacemos el cambio de variable a polares con jacobiano \(r\):

\(\displaystyle V=\iiint_{V}dxdydz=\int_{0}^{h}\int_{0}^{R }\int_{0}^{2\pi}r \ d\theta dr dz=2\pi \int_{0}^{h} \int_{0}^{R}r \ drdz = \)

\(\displaystyle = \pi \cdot R^{2} \cdot \int_{0}^{h} dz= \pi \cdot R^{2} \cdot h\)