El problema de los puentes de Königsberg es uno de los problemas matemáticos más conocidos y analizados, ya que gracias a dicho problema se sentaron las bases de la topología y la teoría de grafos, muy importantes en las matemáticas.
Historia
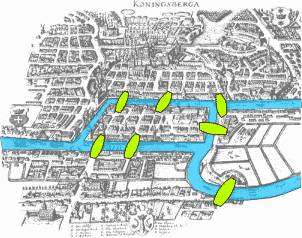
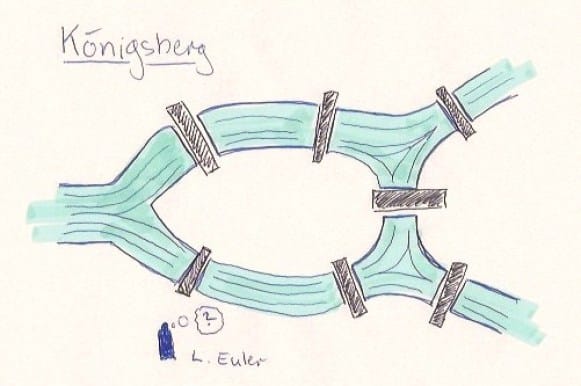
Königsberg (Actualmente Kaliningrado, Rusia) era una ciudad de la antigua Prusia Oriental. Esta ciudad es atravesada por el río Pregel, el cual llega un punto en el que rodea a la isla de Kneiphof para posteriormente separarse en dos ramas, de tal forma que se divide el terreno en 4 regiones. Cada una de las regiones se conectaban entre sí mediante 7 puentes como se indica en la imagen.
El problema
Dado el mapa de Königsberg, con el río Pregel dividiendo el plano en cuatro regiones distintas, que están unidas a través de los siete puentes, ¿es posible dar un paseo comenzando desde cualquiera de estas regiones, pasando por todos los puentes, recorriendo sólo una vez cada uno, y regresando al mismo punto de partida?
¿Crees que puedes resolverlo? Toma un papel y dedícale un par de minutos. No te desesperes si no lo logras
La resolución
Uno de los matemáticos que se encontraban por Königsberg por aquella época era Euler, ya que trabajaba en la Academia Prusiana de las Ciencias.
Al no ser un problema relativamente extenso, puede ser resuelto empleando fuerza bruta (Comprobando todas y cada una de las combinaciones), llegando a la conclusión de que el problema no tiene solución.
Basándose en dicho problema, Euler demostró por qué no tenía solución, y elaboró un teorema que podría aplicarse a cualquier tipo de regiones que quieren ser unidas cumpliendo una serie de normas.
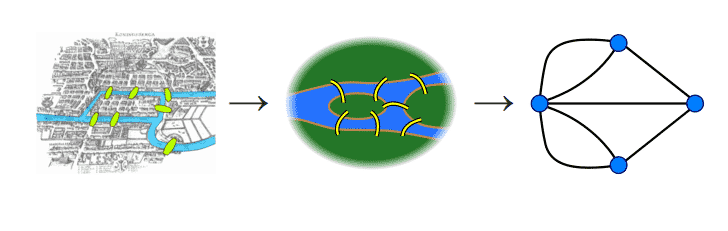
Para poder iniciar el desarrollo, Euler recurre a una abstracción del problema, centrándose en las regiones a unir (Puntos, Nodos) y en los puentes (Líneas, Aristas). Denominamos grado al número de aristas que salen de un nodo.
Teorema 1
Un camino euleriano es un camino que pasa por cada arista una y sólo una vez.
Se dice que un grafo contiene un camino euleriano <=> El grafo es conexo y tiene como máximo una pareja con grado impar
- Un grafo es conexo cuando todos los puntos se conectan entre sí, y no quedan ningunos aislados formando otro grafo
- Es grado par cuando de un nodo parten 2, 4, 6… aristas. Es impar cuando parten 1,3,5… aristas. Se habla de pareja porque si hay uno impar inevitablemente debe de haber otro impar.
Teorema 2
Un ciclo euleriano es un camino euleriano cerrado, es decir, que coincide el punto final e inicial.
Se dice que un grafo contiene un ciclo euleriano <=> El grafo es conexo y todos los nodos presentan grado par
Aplicación
La solución del problema no sólo exige un camino euleriano, sino que además exige que forme un ciclo euleriano (Punto inicial = Punto final), de forma que el grado de los nodos debe de ser par.
Se observa fácilmente que el grado de los nodos es 5,3,3,3. Por lo tanto, el problema no tiene solución.
Pero, ¿Y si quitamos un puente?
Se observa que si quitamos cualquiera de los puentes, se nos queda un grafo con nodos de grado par excepto una pareja de grado impar. En este caso tenemos un camino euleriano, y ciertamente podemos pintar el grafo sin repetir aristas y sin levantar el lápiz. No obstante, el problema no tendría la solución pedida ya que no forma un ciclo euleriano. Es decir, el punto inicial y final no coinciden. Además, otra consecuencia del teorema es que en este caso el punto inicial debe de ser uno de los nodos impares y el punto final debe ser el otro nodo impar.
Ejemplos para practicar
Os dejo una serie de grafos para que saquéis vuestras propias conclusiones. ¿A que ahora los veis con otros ojos? ¡Dejad las soluciones en los comentarios!
1 y 2
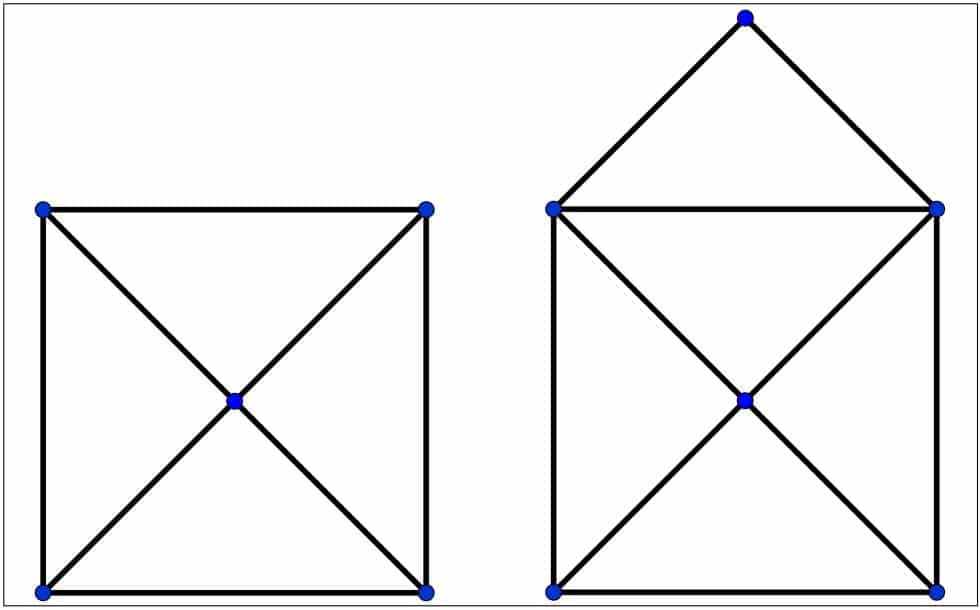
3
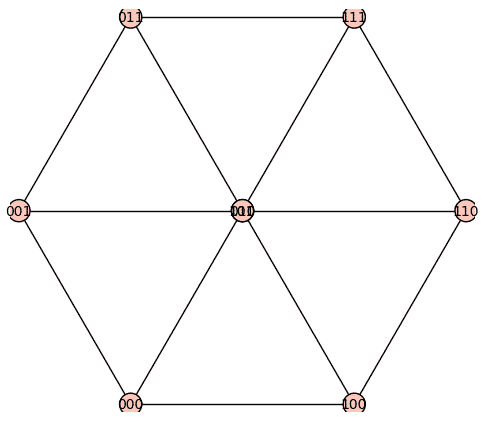
4
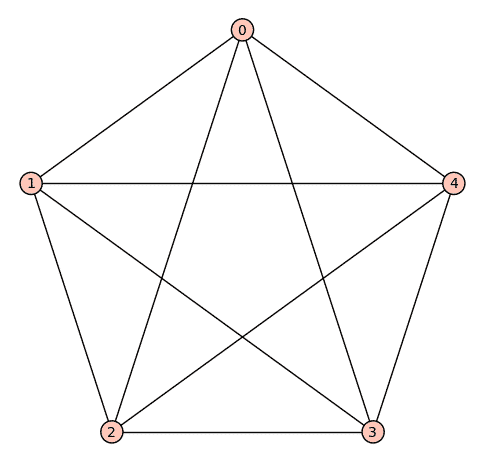
5
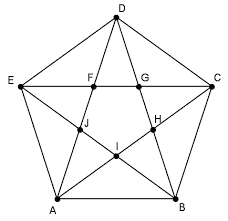
6
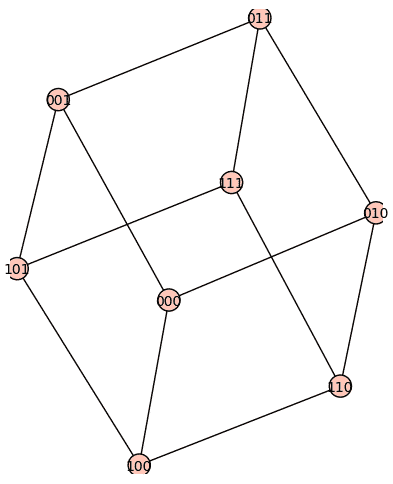
7





Muy buen articulo! Me encantó
Chsm el America
Vien
ñami