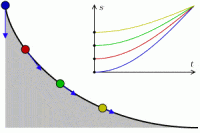
¿Qué es una curva braquistócrona?
La curva braquistócrona (brachistos – ‘el más corto’, chronos – ‘tiempo’) es la curva entre dos puntos tal que, si un cuerpo se deja rodar por efecto de la gravedad de manera ideal (sin rozamiento ni agentes externos) y partiendo de velocidad nula, se recorre en el menor tiempo posible.
Historia de la curva braquistócrona
En 1696, Johann Bernoulli (el mismo Bernoulli que descubrió a Leonhard Euler), propuso un problema como desafío al resto de matemáticos:
Dados dos puntos del plano A y B no alineados vertical ni horizontalmente, existen infinitas curvas que los unen. Se propone hallar, de entre todas las curvas, la que hace mínimo el tiempo de llegada de una bola que parte de A en reposo y llega a B por efecto de la gravedad y sin tener en cuenta el rozamiento.
El problema fue resuelto por el propio Bernoulli y por otros grandes matemáticos como L’Hôpital o Leibniz, así como por el grandísimo Newton quien, para resolver dicho problema, creó el cálculo variacional.
Demostración matemática de la curva braquistócrona
Relación entre velocidades
Para hallar la curva que nos piden necesitamos dar una relación explícita \(y=y(x)\) o paramétrica del tipo:
\( \begin{cases}
y=y(t)\\
x=x(t)
\end{cases} \)
Lo que vamos a hacer en primer lugar es hallar una relación entre la posición de la bola a medida que recorre la curva y el tiempo mínimo. Para ello imaginamos que hacemos “zoom” a mitad de la curva ya con la bola en movimiento y observamos la relación entre velocidades y geometría.
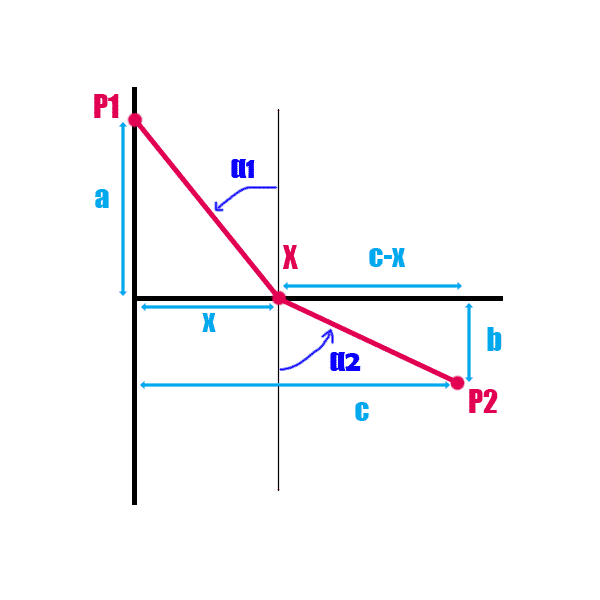
La bola se encuentra en un punto \(P_{1}\) descendiendo con un ángulo \(\alpha_{1}\) con respecto a la vertical a velocidad \(v_{1}\) y tras girar levemente hacia un ángulo de descenso \(\alpha_{2}\) varía su velocidad \(v_{2}\) hasta llegar a un punto \(P_{2}\). Las coordenadas de los puntos son, en base al sistema de referencia de la imagen:
\(\begin{cases} P_{1}=(0,a) \\ P_{2}=(c,-b)\end{cases}\)El punto \(X\) es el punto de coordenadas \(X=(x,0)\) en el cual se realiza el cambio de ángulo y simplemente sirve como punto “virtual” para definir la relación entre ángulos.
El tiempo que tarda la bola en ir de \(P_{1}\) a \(P_{2}\) es el tiempo de \(P_{1}\) a \(X\) + el tiempo de \(X\) a \(P_{2}\) . El tiempo que se tarda en recorrer cada uno de los dos tramos se obtiene simplemente dividiendo la longitud del tramo entre la velocidad.
\(T=T(x)=\dfrac{\sqrt{a^{2}+x^{2}}}{v_{1}} + \dfrac{\sqrt{b^{2}+(c-x)^{2}}}{v_{2}}\)
Dicho tiempo es una función que, fijadas las coordenadas de los puntos, depende exclusivamente de \(x\).
Si queremos buscar el mínimo simplemente debemos derivar e igualar a cero:
\(\dfrac{dT}{dx}=0=\dfrac{x}{v_{1} \sqrt{ a^{2}+x^{2} }} – \dfrac{c-x}{\sqrt{ b^{2}+(c-x)^{2} }}=0 \iff\)
\(\iff \dfrac{x}{v_{1} \sqrt{ a^{2}+x^{2} }} = \dfrac{c-x}{\sqrt{ b^{2}+(c-x)^{2} }} \)
Geométricamente, la relación entre las longitudes y el seno de los ángulos es:
\(\begin{cases} sin(\alpha_{1}) = \dfrac{x}{\sqrt{a^{2}+x^{2}}} \\ sin(\alpha_{2}) = \dfrac{c-x}{\sqrt{b^{2}+(c-x)^{2}}} \end{cases}\)De forma que la relación entre geometría y velocidad que minimiza el tiempo de desplazamiento es:
\(\dfrac{ sin(\alpha_{1}) }{v_{1}} = \dfrac{ sin(\alpha_{2}) }{v_{2}} = \dfrac{ sin(\alpha) }{v} = cte\)
Es decir, que la relación entre el ángulo de incidencia y la velocidad de incidencia sea constante. Al inicio con velocidad nula interesa una caída vertical (ángulo con respecto a la vertical nulo) y a medida que aumenta la velocidad se va suavizando el ángulo. Esta fórmula coincide de hecho con la Ley de Snell (refracción), descubierta experimentalmente y que cumple el Principio de de Fermat o de Menor Tiempo: La luz tiende a escoger el camino por el cuál llega antes. Impresionante. ¿no?
Además, al ser dicha relación siempre constante en todo momento, las variables de ángulo y velocidad no tienen por qué ser valores discretos sino que pueden ser variables continuas, pudiendo aplicar dicha fórmula a una curva de curvatura suave (y no a trompicones como sucedería si la evolución fuese como la imagen).
Obtención de la braquistócrona
Antes de comenzar el estudio hay que introducir algo de física en el problema ya que se ven involucradas magnitudes relacionadas con el movimiento. En un entorno ideal la energía mecánica permanece constante, y eso implica que la velocidad que adquiere la partícula va a depender exclusivamente de la disminución de altura.
Aplicando lo expuesto anteriormente y considerando \(y\) como la disminución en altura:
\(E_{c} – E_{p} = 0 = \dfrac{1}{2} m v^{2} – m g y \iff \)
\( \iff v^{2} = 2 g y \rightarrow v= \sqrt{2 g y}\)
Una vez relacionadas la velocidad con la altura gracias a la física, volvemos al problema geométrico. Si observamos la imagen, la relación entre la pendiente de la curva y el ángulo de la tangente es tal que
\(\dfrac{dx}{dy} = tan(\alpha)\)
Si desarrollamos la tangente y lo expresamos todo en base al \(sin(\alpha)\) gracias a la fórmula fundamental de la trigonometría:
\(tan(\alpha) = \dfrac{sin(\alpha)}{cos(\alpha)} = \dfrac{sin(\alpha)}{\sqrt{1-sin^{2}(\alpha)}}\)
Sabiendo del desarrollo anterior la relación entre ángulo y velocidad que minimiza el tiempo y sustituyendo el seno en la ecuación
\(\dfrac{sin(\alpha)}{v}=k \rightarrow sin(\alpha) = k \cdot v\)
\(\dfrac{dx}{dy} = \dfrac{k \cdot v}{\sqrt{1-k^{2} \cdot v^{2}}} \)
Escribiendo ahora \(v\) en función de \(y\):
\(\dfrac{dx}{dy} = \dfrac{k \cdot \sqrt{2 g y} }{\sqrt{1-k^{2} \cdot 2 g y}} \)
Dividiendo el numerador y denominador entre \(k \sqrt{2g}\) y definiendo la constante \(K\) como producto de las otras constantes:
\(\dfrac{dx}{dy} = \dfrac{\sqrt{y} }{\sqrt{\dfrac{1}{k^{2} \cdot 2 g}- y}} = \sqrt{\dfrac{y}{K-y}} \)
Por lo tanto, basta integrar para obtener una relación \(x=x(y)\)
\(\displaystyle x(y) = \int dx = \int \sqrt{\dfrac{y}{K-y}} dy \)
Haciendo el cambio de variable:
\(\begin{cases} y=K sin^{2} (t) \\ dy=2 K sin(t) cos(t) dt \end{cases}\)\(\displaystyle x(y) = \int \sqrt{\dfrac{ K sin^{2} (t) }{K- K sin^{2} (t) }} 2 K sin(t) cos(t) dt =\)
\(\displaystyle = 2 K \int sin^{2}(t) dt = 2 K \int 1-cos^{2}(t) dt = 2 K \int 1- \left [\dfrac{1+cos(2t)}{2} \right ] dt =\)
\( = 2K \left (\dfrac{1}{2} t – \dfrac{sin(2t)}{4} \right )\)
Llegando a las ecuaciones paramétricas:
\(\begin{cases} x(t)= 2K \left (\dfrac{1}{2} t – \dfrac{sin(2t)}{4} \right ) = \dfrac{K}{2} (2t – sin(2t)) \\ y(t)=K sin^{2} (t) = \dfrac{K}{2} (1- cos(2t)) \end{cases}\)Que representa, para cada valor de \(K\), la ecuación de una Cicloide, que es la curva “pintada” por un punto fijo de una circunferencia que se desplaza rotando. Esta curva tiene muchas otras propiedades y es conocida desde la antigüedad.
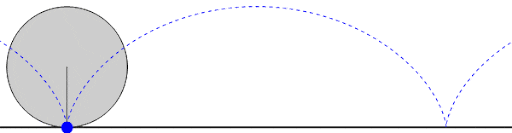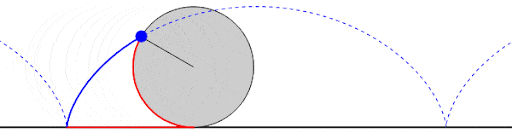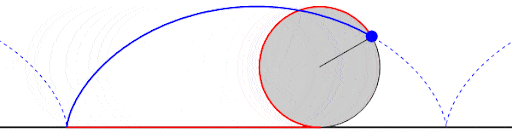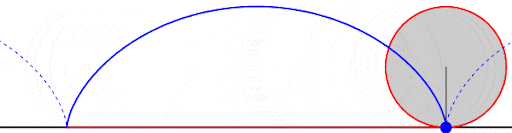
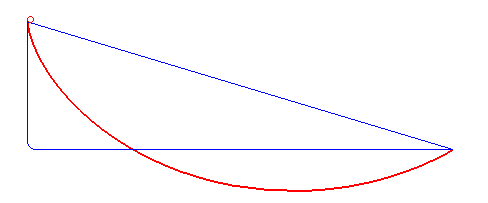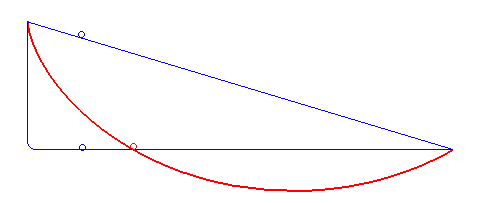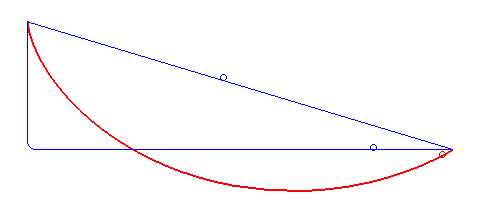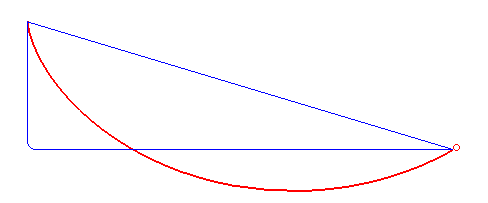
La tautócrona
Una tautócrona o curva isócrona (tauto-/iso- mismo y chronos tiempo) es una curva para la cual el tiempo tomado por una bola que desliza sin rozamiento por efecto de la gravedad hasta el punto más bajo es independiente de su punto de partida. Esta curva también es sorprendentemente una cicloide.
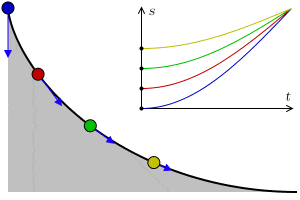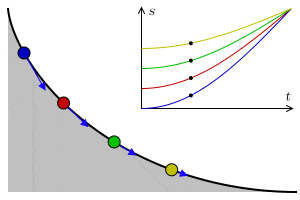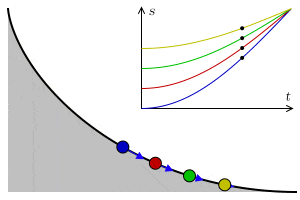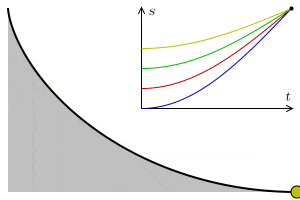
Esta propiedad recuerda a la de un péndulo, que para pequeñas oscilaciones su tiempo de oscilación depende exclusivamente de la longitud de la cuerda y del valor de la gravedad, no del punto de partida.
\({\displaystyle t=\pi {\sqrt {\frac {r}{g}}}}\)
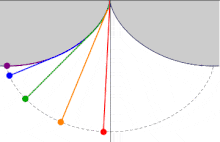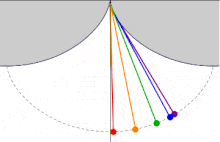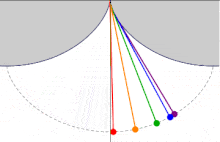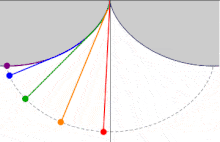
Es alucinante que la misma curva tenga estas dos propiedades tan interesantes. ¿Qué te parece? ¿Son las matemáticas tan aburridas como te pensabas? ¡En el próximo artículo demostraré matemáticamente la propiedad de la tautócrona para aquellos escépticos!