El ladrillo de Euler es un ortoedro en el que tanto las longitudes de las aristas como de sus diagonales son números enteros. En este artículo vamos a desarrollar un análisis acerca del ladrillo de Euler y veremos problemas relacionados como el cuboide perfecto o ladrillo de Euler perfecto.
Introducción al ladrillo de Euler
Un ortoedro es un prisma rectangular ortogonal, cuyas caras forman entre sí ángulos diedros rectos. Un claro ejemplo de ortoedro es una caja de zapatos. Un cubo es un caso especial de ortoedro, de seis caras cuadradas iguales.
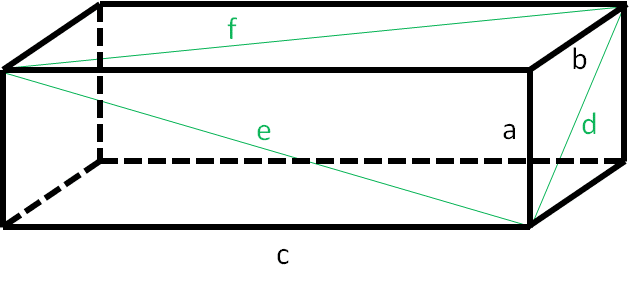
Un ladrillo de Euler, nombrado así en honor a Leonhard Euler, es un ortoedro cuyas aristas y diagonales de cara tienen longitudes enteras. Un ladrillo de Euler primitivo es aquel cuyas longitudes de arista son números primos entre sí. La relación entre aristas y diagonales es la siguiente:
\(a^{2} + b^{2} = d^{2}\)
\(a^{2} + c^{2} = e^{2}\)
\(b^{2} + c^{2} = f^{2}\)
Por lo tanto, el problema a resolver es encontrar 3 números naturales \(a, b, c\) tal que:
\(d = \sqrt{a^{2} + b^{2}}, \ \ e = \sqrt{a^{2} + c^{2}}, \ \ f = \sqrt{b^{2} + c^{2}}\)
Son números enteros positivos.
El ladrillo de Euler más pequeño lo descubrió, en el año 1719, el matemático Paul Halcke y presenta las siguientes dimensiones:
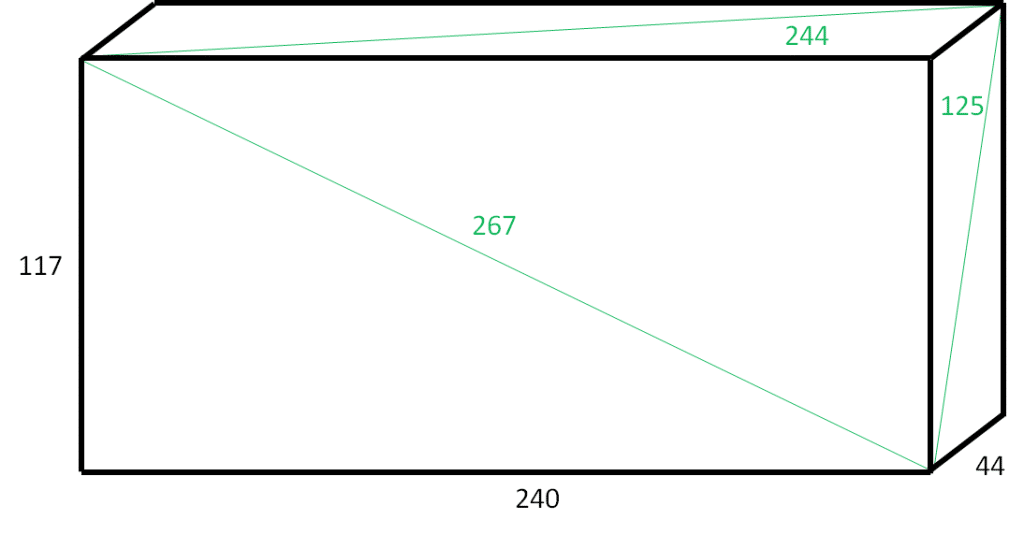
\(a = 117, \ \ b = 44, \ \ c = 240\)
\(d = \sqrt{117^{2} + 44^{2}} = 125\)
\(e = \sqrt{117^{2} + 240^{2}} = 267\)
\(f = \sqrt{44^{2} + 240^{2}} = 244\)
A continuación se presentan otros ejemplos de ladrillos de Euler:
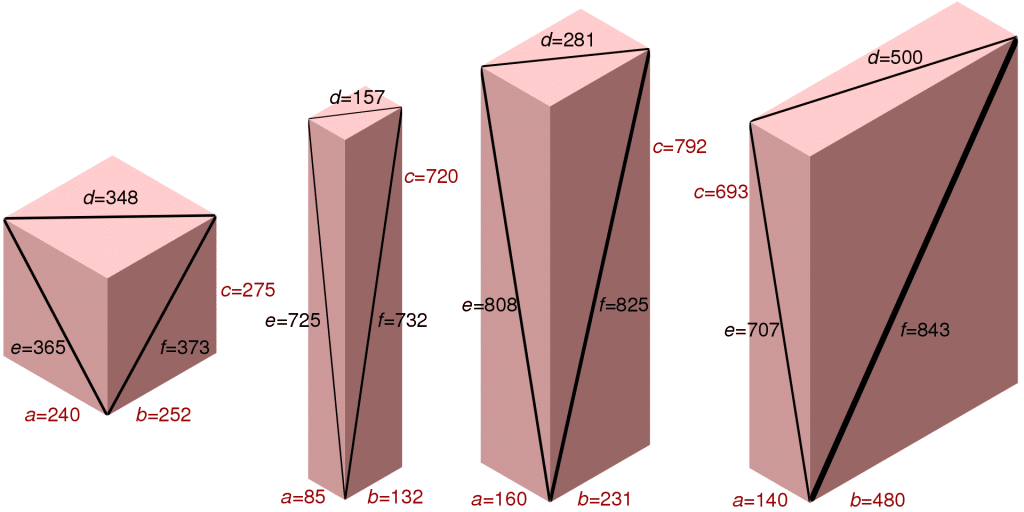
Propiedades del ladrillo de Euler y cómo hallar sus dimensiones
Terna pitagórica
Una terna pitagórica es un conjunto ordenado de tres números enteros positivos \(u, v, w\) que son solución de la ecuación diofántica cuadrática:
\(u^{2} + v^{2} = w^{2}\)
Recibe ese nombre porque dicha ecuación se relaciona con el Teorema de Pitágoras, y a sus soluciones \(u, v, w\) se les llama números pitagóricos. Las ternas cuyos tres números son primos relativos son denominados ternas pitagóricas primitivas. Ejemplos de ternas pitagóricas primitivas son:
\((3, 4, 5) \ \ \ \ (5, 12, 13) \ \ \ \ (8, 15, 17) \ \ \ \ (7, 24, 25)\)
Dado un valor de \(j\) entero (natural), Pitágoras encontró infinitas soluciones al problema en la forma de tres ecuaciones:
\(\begin{cases}u & =j^{2}-1\\ v & =2j\\ w & =j^{2}+1\end{cases}\)No obstante, dicho método no garantiza la obtención de todas las ternas Pitagóricas. Por ejemplo, la terna \((5, 12, 13)\) no es obtenible por dicho método. Hay otro método, que consiste en elegir 2 números \(m > n\) enteros positivos, de forma que el siguiente conjunto es una terna pitagórica:
\(\begin{cases}u & =m^{2} – n^{2} \\ v & =2mn \\ w & =m^{2}+n^{2}\end{cases}\)Obsérvese que realmente el primer método es este segundo método fijando \(n=1\). Las ternas propuestas de ejemplo serían las generadas con los valores:
\(m, n = (2,1), \ \ (3,2), \ \ (4,1), \ \ (4,3)\)
La terna pitagórica generada será primitiva si y solo si \(m, n\) son coprimos y solamente uno de ellos es par (si ambos \(m, n\) son impares, entonces \(u, v, w\) serán pares, y la terna no será una terna pitagórica primitiva al tener como máximo común divisor el 2).
Ecuación generadora de ladrillos de Euler
Dada una terna pitagórica \(u, v, w\), Nicholas Saunderson obtuvo unas ecuaciones paramétricas para obtener las dimensiones de un ladrillo de Euler. Dichas ecuaciones son:
\(\begin{cases}a & = u |4v^{2} -w^{2}| \\ b & = v |4u^{2} – w^{2}| \\ c & = 4uvw \end{cases}\)Si calculamos las diagonales y simplificamos, su valor es:
\(\begin{cases}d & = w^{3} \\ e & = u (4v^{2} + w^{2}) \\ f & = v (4u^{2} + w^{2}) \end{cases}\)Por ejemplo, si partimos de la terna \( (5, 12, 13)\), obtenemos el siguiente ladrillo de Euler:
\(a = 2035, \ \ b = 828, \ \ c = 3120\)
\(d = 2197, \ \ e = 3725, \ \ f = 3228\)
Cabe destacar que dicha ecuación permite generar infinitos ladrillos de Euler partiendo de cualquier terna pitagórica, la cuál a su vez se puede generar a partir de infinitos valores de \(j\) o de \((m, n)\). No obstante, no todos los ladrillos de Euler son generados por dicha ecuación. El ladrillo \((240, 252, 275)\) es un ejemplo de ello.
Si \((a,b,c)\) son las dimensiones de un ladrillo de Euler, entonces un ortoedro de dimensiones multiplicadas por \(k\): \((k a, k b, k c)\) es también un ladrillo de Euler. Si para que un ortoedro sea un ladrillo de Euler se tiene que cumplir que:
\(d = \sqrt{a^{2} + b^{2}}, \ \ e = \sqrt{a^{2} + c^{2}}, \ \ f = \sqrt{b^{2} + c^{2}}\)sean números enteros, partiendo de que lo son, si sustituimos \((k a, k b, k c)\) obtenemos:
\(d = k \sqrt{a^{2} + b^{2}}, \ \ e = k \sqrt{a^{2} + c^{2}}, \ \ f = k \sqrt{b^{2} + c^{2}}\)Siendo por lo tanto también números enteros. Los ladrillos de Euler tienen otras propiedades cuyo desarrollo puede encontrarse aquí.
El ladrillo de Euler perfecto
Un ladrillo de Euler perfecto es un ladrillo de Euler cuya diagonal espacial es también un número entero. Es decir, que debe cumplirse que:
\(d = \sqrt{a^{2} + b^{2}}, \ \ e = \sqrt{a^{2} + c^{2}}, \ \ f = \sqrt{b^{2} + c^{2}}, \ \ g = \sqrt{a^{2} + b^{2} + c^{2}}\)
sean todos números enteros.
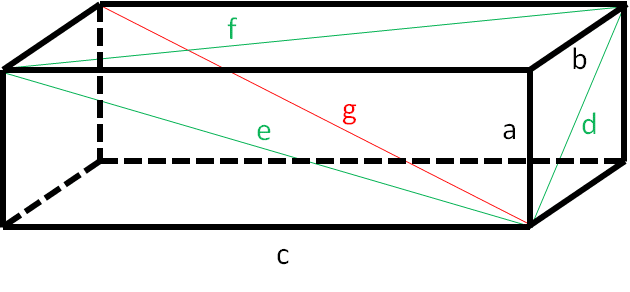
A día de hoy, no sólo no se ha encontrado ningún ladrillo de Euler perfecto, sino que tampoco ha sido posible demostrar que pueda obtenerse o no.
No obstante, por fuerza bruta se ha demostrado que, si un ladrillo de Euler perfecto existe, debe cumplirse que:
- El lado pequeño debe ser mayor que \(5 \cdot 10^{11}\)
- El lado impar debe ser mayor que \(2.5 \cdot 10^{13}\)
- la diagonal espacial debe ser mayor que \(9 \cdot 10^{15}\)
Hay muchas otras propiedades de divisibilidad y relación entre las aristas que algebraicamente puede demostrarse que dichos ladrillos deben cumplir, y que ayudan a reducir enormemente la búsqueda. No obstante, el tamaño de las cifras mencionadas nos da una idea de la complejidad de la búsqueda.
Hay otro tipo de cuboides, llamados cuboides casi perfectos, en los que 6 de estas 7 dimensiones \((a, b, c, d, e, f, g)\)son números enteros. Por ejemplo, es posible que todas las diagonales, incluyendo la espacial, así como 2 aristas sean números enteros, o que todas las aristas y diagonales excepto una sean números enteros.
Repercusiones de encontrar un ladrillo de Euler perfecto
Hay muchos problemas en las matemáticas como este que parecen acertijos algebraicos o pequeños juegos que llaman la atención de los matemáticos y los afrontan como retos. No obstante, detrás de una demostración, hay un trasfondo teórico brutal así como grandes repercusiones en las matemáticas. Obtener las dimensiones de un ladrillo de Euler perfecto no sólo supondría un “logro”, sino que:
- El descubrimiento de un ladrillo de Euler perfecto sería un avance significativo en teoría de números y geometría, proporcionando una comprensión más profunda de las propiedades de las ternas pitagóricas y sus relaciones con las ecuaciones diofánticas.
- Los ladrillos de Euler perfectos están vinculados al teorema de Pitágoras, lo que implica aplicaciones en geometría euclidiana y la posibilidad de nuevas construcciones geométricas y demostraciones.
- Aunque no directamente aplicable, podría inspirar enfoques matemáticos dentro de la física teórica y encontrar aplicaciones en campos como la cristalografía.
- Podría mejorar algoritmos para encontrar ternas pitagóricas, lo que tendría aplicaciones en criptografía, teoría de códigos y geometría computacional.
A pesar de ser un problema tan antiguo y bastante estudiado, eso no significa que no pueda obtenerse una solución. Podría ponerse como ejemplo la Conjetura de Poincaré (1904), uno de los 7 problemas del milenio que fue resuelto en 2003.