El Teorema de Bayes es una herramienta fundamental en la estadística, que permite actualizar la probabilidad de una hipótesis en función de la evidencia disponible. Fue definido por el matemático y estadístico inglés Thomas Bayes en el siglo XVIII, pero su utilidad y relevancia se extienden hasta nuestros días, y se aplica en una amplia variedad de campos, como la medicina, la inteligencia artificial y la economía, entre otros.
En esencia, el teorema de Bayes establece una relación entre la probabilidad de una hipótesis o evento, y la probabilidad de la evidencia, dadas ciertas condiciones previas. En otras palabras, nos permite actualizar nuestra creencia sobre una hipótesis a medida que obtenemos nueva información relevante.
En este artículo, exploraremos con mayor detalle los fundamentos del teorema de Bayes, su aplicación en diferentes áreas, y algunos ejemplos prácticos que ayuden a comprender su utilidad y aplicabilidad.
Conceptos básicos de probabilidad
La probabilidad es un concepto fundamental en estadística y matemáticas en general que nos permite cuantificar la incertidumbre asociada a eventos o resultados. Al conjunto de posibles sucesos mutuamente excluyentes \(A_{i}\) se le denomina espacio muestral y se denota por:
\(E = \{A_{1}, A_{2} … A_{n}\} = A_{1} \cup A_{2} \cup … \cup A_{n}\)
Siendo \(A_{i}\) cada uno de los posibles eventos o resultados de un experimento. La probabilidad de que un evento \(A_{1}\) tenga lugar se define como el número de situaciones en las que el evento \(A_{1}\) tiene lugar (\(n(A_{1})\)) dividido entre el número total de situaciones, es decir:
\(\displaystyle P(A_{1}) = \dfrac{n(A_{1})}{\sum n(A_{i})}\)
Pongamos el ejemplo de un dado de 6 números: 1,2,3,4,5 y 6. La probabilidad de que al lanzarlo salga un 3 es de:
\(P(3) = \dfrac{1}{6}\)
Puesto que sólo hay un 3 en el dado y pueden salir 6 resultados diferentes con la misma probabilidad.
Por otra parte, la probabilidad de que salga un número par es de:
\(P(par) = \dfrac{3}{6} = \dfrac{1}{2}\)
Puesto que pueden salir 3 números pares (2,4 y 6) entre los 6 posibles resultados.
No obstante, hay situaciones en las que la ocurrencia de un evento depende de otros eventos, y por lo tanto la probabilidad de que algo suceda no es independiente. Es entonces cuando se define la probabilidad condicional y según el teorema de Bayes:
Dada una partición \(A_{1}, A_{2} … A_{n}\) del espacio muestral, y dado un suceso cualquiera \(B\), el teorema de Bayes expone:
\(P(A_{i}|B) = \dfrac{P(A_{i} \cap B)}{P(B)} = \dfrac{P(A_{i}) P(B|A_{i})}{\sum P(A_{k}) P(B|A_{k})}\)
El desarrollo del denominador viene dado de la siguiente manera:
\(\sum P(A_{k}) P(B|A_{k}) = \sum \left (P(A_{k}) \dfrac{P(B \cap A_{k})}{P(A_{k})} \right ) = \sum P(B \cap A_{k}) = P(B) \)
Finalmente, otra relación entre probabilidades que surge de aplicar dicho Teorema es la equivalencia entre probabilidades condicionales. Se tiene que:
\(P(A_{i}|B) = \dfrac{P(A_{i} \cap B)}{P(B)} \rightarrow P(A_{i} \cap B) = P(A_{i}|B) P(B)\) \(P(B|A_{i}) = \dfrac{(B \cap A_{i})}{P(A_{i})} \rightarrow P( B \cap A_{i}) = P(A_{i} \cap B) = P(B|A_{i}) P(A_{i}) \iff\)\(\iff P(A_{i}|B) P(B) = P(B|A_{i}) P(A_{i})\)
Lo cuál es extremadamente útil para calcular probabilidades de hechos que no se conocen cuando se conoce el complementario.
Para comprender mejor estos cálculos se va a poner un ejemplo. En una fábrica se fabrican coches y motos. El 40% de la producción son coches y el 60% son motos. Además, cada vehículo lo pintan de negro o de blanco. En el caso de los coches, el 10% de los coches los pintan de blanco y el 90% de negro, mientras que en las motos el 60% las pintan de negro y el 40% de blanco.
Si se elige al azar un vehículo que ha salido de producción, ¿Qué probabilidades hay de que sea un vehículo negro?
El esquema con las probabilidades se muestra a continuación:
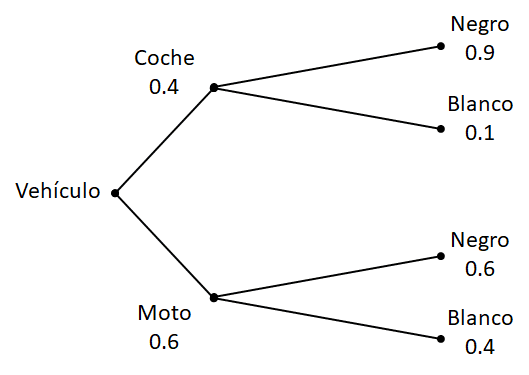
Denominamos \(C\) a coches, \(M\) a motos, \(N\) a negros, \(B\) a motos. La probabilidad de que el color sea negro sabiendo que es un coche lo denotamos como \(P(N|C)\) y la probabilidad de que el vehículo fuese una moto sabiendo que el vehículo es negro se denotaría \(P(M|N)\). El resumen de probabilidades que salen instantáneamente de los datos del enunciado es el siguiente:
\(P(C) = 0.4\)
\(P(M) = 0.6\)
\(P(N|C) = 0.9\)
\(P(B|C) = 0.1\)
\(P(N|M) = 0.6\)
\(P(B|M) = 0.4\)
Y lo que queremos calcular es la probabilidad de que salga un vehículo negro. Esto se calcularía como:
\(P(N) = P(N|C) P(C) + P(N|M) P(M) = 0.9 \cdot 0.4 + 0.6 \cdot 0.6 = 0.72\)
Es decir, un 72%. Por lo tanto, la probabilidad de que fuese blanco sería del 28% y se podría calcular directamente como \(1-0.72 = 0.28\). De todas formas, la vamos a calcular aplicando el teorema para ver su funcionamiento:
\(P(B) = P(B|C) P(C) + P(B|M) P(M) = 0.1 \cdot 0.4 + 0.4 \cdot 0.6 = 0.28\)
Prior, Likelihood y Posterior
En muchos artículos acerca de probabilidad Bayesiana se mencionan estos conceptos. En español se suelen denominar probabilidad a priori (Prior), probabilidad en la hipótesis (Likelihood) y probabilidad a posteriori (Posterior).
La probabilidad a priori o Prior se llama a la probabilidad de que suceda un evento sin tener más información. Es decir, sería \(P(A)\).
La probabilidad a posteriori o Posterior sería la probabilidad de que suceda dicho evento sabiendo que ha ocurrido otro que tiene cierto efecto en él, es decir, \(P(A|B)\).
La probabilidad en la hipótesis o Likelihood es la probabilidad de que sucediese el otro evento sabiendo que se ha producido el evento de interés, es decir, \(P(B|A)\).
Finalmente, hay una probabilidad que suelde denominarse de evidencia o marginal y hace referencia a la probabilidad de que suceda este otro evento secundario, \(P(B)\), que sirve para normalizar la probabilidad en la hipótesis y que permite expresar la relación entre todas:
Posterior = Prior * Likelihood/Marginal
O lo que es lo mismo, el teorema de Bayes:
\(P(A|B) = \dfrac{P(B|A) P(A)}{P(B)}\)
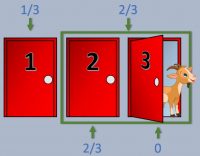
Problema de Monty-Hall usando el Teorema de Bayes
Hace un tiempo se analizó en este blog el Problema de Monty-Hall y si se podría aplicar a un tipo test. Sin embargo, se dedujo la solución más bien de palabra / lógica sin entrar en aspectos matemáticos.
El enunciado es el siguiente: 3 puertas y sólo una de ellas tiene un premio. Una vez elegimos una puerta al azar, abren la puerta vacía de las 2 restantes. Nos preguntan entonces: ¿Quieres cambiar tu elección a la otra puerta que queda sin abrir o te mantienes en la elección original?
Aquí claramente hay dos probabilidades, la probabilidad a priori de que el premio esté en la puerta original, y la probabilidad a posteriori de que el premio esté en la puerta original, y lo interesante es entonces cuantificarla para saber si seguir con esa puerta o cambiarnos.
Digamos que la probabilidad de que el premio esté en la puerta original es \(P(A) = 1/3\) puesto que a priori no tenemos ninguna información de nada y podría estar en cualquier puerta con la misma probabilidad.
Vamos a denominar como \(P(B)\) a la probabilidad de que la puerta que se abre está vacía, y lo que queremos calcular es la probabilidad de que el premio esté en la puerta original sabiendo que la puerta que se abre no tiene premio, es decir:
\(P(A|B) = \dfrac{P(A \cap B)}{P(B)} = \dfrac{P(B|A)P(A)}{P(B)}\)
Como hemos dicho, la probabilidad a priori de que la puerta original tuviera premio era \(P(A) = 1/3\). Por otra parte, la puerta que se abre siempre está vacía, por lo que \(P(B) = 1\). Además, la probabilidad de que la puerta que abren esté vacía si la original tiene premio seguirá siendo máxima, por lo tanto \(P(B|A) = 1\). Finalmente, la probabilidad resulta:
\(P(A|B) = \dfrac{1 \cdot 1/3}{1} = \dfrac{1}{3}\)
Es decir, que si nos mantenemos con la puerta original, nuestra probabilidad seguirá siendo de 1/3 como al inicio. No obstante, si cambiamos de puerta, nuestra probabilidad pasará a ser 2/3 al ser el complementario. Del mismo modo se podría calcular dicha probabilidad empleando la misma lógica y expresando como \(P(\bar{A})\) a la probabilidad a priori de que no esté en la puerta original:
\(P(\bar{A}|B) = \dfrac{P(B|\bar{A})P(\bar{A})}{P(B)} = \dfrac{1 \cdot 2/3}{1} = \dfrac{2}{3}\)
La Paradoja del Falso Positivo
Para finalizar este artículo me gustaría analizar un problema de probabilidad que es bastante contraintuitivo pero que, como siempre decimos por aquí, las matemáticas nunca mienten. Dicho problema se denomina la Paradoja del falso positivo.
La paradoja del falso positivo es un problema de estadística cuya solución arroja que en determinados casos, es más probable que el test que indica que tenemos una enfermedad sea incorrecto (falso positivo) a que tengamos la enfermedad.
Esto es bastante contraintuitivo porque si nos hacemos una prueba y sale que somos positivos, lo más probable es que lo seamos. Es cierto que ningún test es 100% perfecto, pero lo que no tendría ningún sentido es que a pesar de dar positivo fuera mucho más probable que no lo fuéramos. Y esto es lo que sucede en estos casos.
Digamos que se descubre que hay un gen que hace que las personas en edad adulta desarrollen un tipo de cáncer. Tras numerosos estudios exhaustivos en diferentes grupos de personas, se sabe a ciencia cierta que aproximadamente un 0,1% de la población presenta dicho gen. Una empresa farmacéutica ha desarrollado un test rápido que te permite saber en segundos si tienes dicho gen o no. No obstante, dicho test tiene una precisión del 99%.
Como te preocupas por tu futuro te compras el test y el resultado arroja que eres positivo. Sabiendo esta información, ¿Qué probabilidades hay de que tengas dicho gen?
Definimos la probabilidad de tener el gen como \(P(G) = 0.001\), y la probabilidad de que el test sea correcto como \(P(C) = 0.99\). Por otra parte, definimos la probabilidad de que el test sea positivo como \(P(P)\). El valor que nos interesa calcular es \(P(G|P)\), es decir, la probabilidad de tener el gen sabiendo que el test es positivo.
\(P(G|P) = \dfrac{P(P|G) P(G)}{P(P)}\)
\(P(P|G) = 0.99\)
\(P(G) = 0.001\)
\(P(P) = P(P|G)*P(G) + P(P|\bar{G})*P(\bar{G}) = 0.99*0.001 + 0.01*0.999 = 0.01098\)
El resultado resulta:
\(P(G|P) = \dfrac{P(P|G) P(G)}{P(P)} = \dfrac{0.99 * 0.001}{0.01098} = 0.0901\)
Es decir, que la probabilidad de tener el gen sería sólo del 9% en caso de ser positivo. Este es un resultado extremadamente sorprendente por lo que se comentó al inicio, y tiene un efecto brutal en la concepción de pruebas y análisis de los resultados. Es un ejemplo más de anumerismo y cómo no deberíamos de fiarnos puramente de nuestra lógica en temas estadísticos.
Sólo imaginaos que la situación fuese real y una empresa se estuviese lucrando vendiendo unos tests que no garantizan absolutamente nada… Sería indignante. ¿Y la cantidad de estadísticas falsas que saldrían?