Seguro que muchos de mis lectores habrán visto la película de 21 blackjack (y los que no, ¡estáis tardando!). Y, tanto aquellos que la vieron, como aquellos otros que no pero que suelen ver vídeos virales, seguro que se acuerdan de haber visto esta escena:
El problema está claro pero quizás la solución no es tan intuitiva. En este artículo comprenderás por qué lo que se ve en el vídeo es cierto.
Mi amigo Nico, tras ver la película, pensó que esta misma deducción podría emplearse en un examen de tipo test, agrupando respuestas, descartando una de ellas y asegurándose una probabilidad de acierto mayor. Tiene sentido. Sin embargo, no es cierto. Es una malinterpretación del problema y de las condiciones de este. Veremos por qué no funciona.
El Problema de Monty-Hall
El problema de Monty Hall o paradoja de Monty Hall es un problema matemático de probabilidad basado en el concurso televisivo estadounidense Trato hecho (Let’s Make a Deal). El problema fue planteado y resuelto por el matématico Steve Selvin, pero fue bautizado con el nombre del presentador de dicho concurso, Monty Hall.
Planteamiento
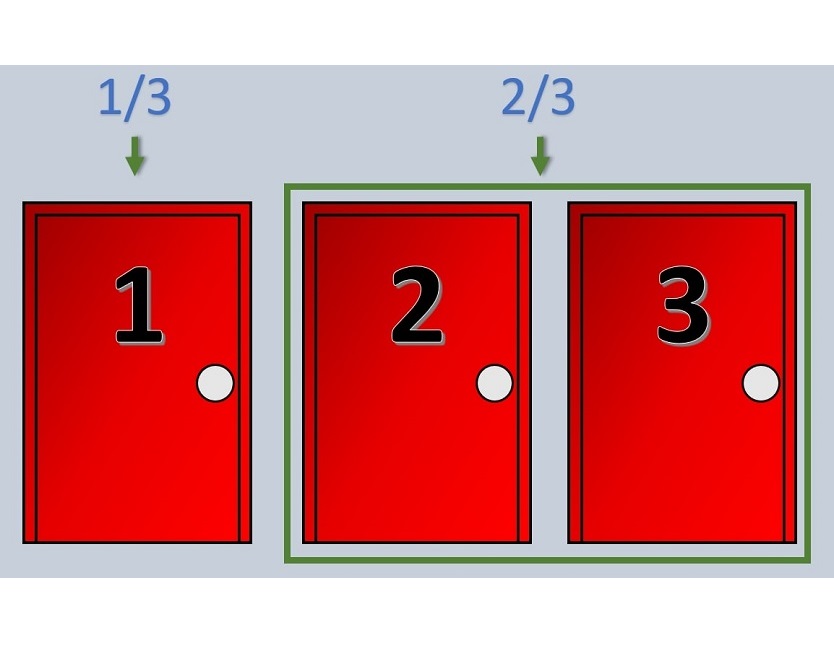
Al concursante se le da la opción de elegir una puerta ente tres. El premio consiste en llevarse lo que hay detrás de la puerta. Se sabe que detrás de una de las puertas hay un coche y detrás de las otras dos puertas hay cabras. Una vez que el concursante ha elegido una puerta y comunicado su elección, el presentador, que sabe qué hay detrás de cada puerta, decide abrir una de las otras dos puertas que han quedado sin elegir y abrirá la que contenga una cabra.
A continuación, le da al concursante la posibilidad de cambiar su elección. Puede mantener la puerta que eligió o cambiar su elección a la otra perta que queda por abrir. ¿Qué debería de hacer?¿Hay alguna diferencia?
Resolución y demostración
Uno, con una de las puertas abiertas y sólo 2 cerradas, tiende a “resetear” el problema y pensar que tiene un 50% de acertar ya que hay 2 puertas y él no tiene ni idea. Sin embargo, si empleamos la estadística, que nos hayan abierto una de las puertas supone una ventaja enorme.
Antes de nada vamos a resumir las premisas del problema:
- El presentador siempre abre una puerta
- Detrás de la puerta que abre siempre hay una cabra
- La puerta que abre el presentador es una de las que se han quedado libres
La probabilidad de que el concursante acierte en su primera elección es de 1/3 mientras que hay 2/3 de probabilidad de que haya fallado, es decir, que esté en una de las otras dos puertas. ¿Qué cambia el hecho de que el presentador abra una de las otras dos puertas? Pues lo cambia todo, porque lo hace después de esa primera elección. Esto es, la elección del jugador afecta a la puerta que abre el presentador. No es un suceso aleatorio ni inconexo.
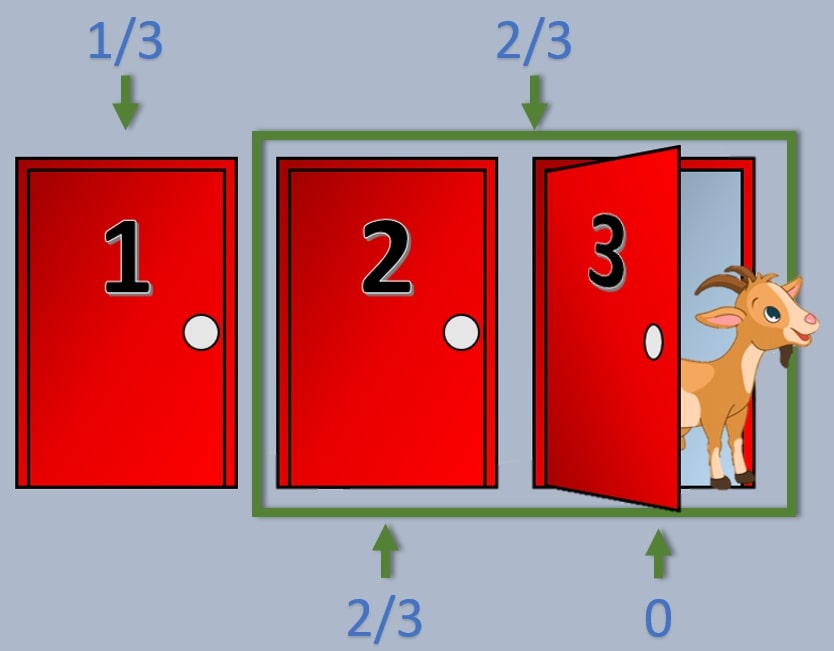
-Si el jugador en su primera elección elige la puerta con el coche (1/3 de acertar), el presentador abre cualquiera de las otras dos puertas, y el jugador pierde si cambia la elección.
-Si el jugador en su primera elección falla (2/3 de fallar), el presentador abre la otra puerta que contiene la cabra, y el jugador gana si cambia la elección.
Es decir, que si el jugador siempre cambia, tiene 1/3 de perder y 2/3 de ganar, siendo más beneficioso cambiar la elección. Si siempre cambias tu elección es como si realmente te dieran la posibilidad de elegir 2 puertas desde un principio, siendo la probabilidad de acierto de 2/3.
La explicación empleando el Teorema de Bayes con matemáticas de manera rigurosa se encuentra en el siguiente artículo:
Aplicabilidad del problema de Monty-Hall en un examen de tipo test
El problema básico está claro y no admite debate alguno. Son matemáticas y las matemáticas nunca fallan.
Ahora surge la idea de aplicar este mismo problema o concepto a una situación cotidiana en la que nos podamos ver beneficiados. Y la primera idea está clara: en un examen tipo test. Pero… ¿Cómo se podría aplicar?
Condiciones del tipo test
- Para cada pregunta hay 3 posibles respuestas.
- Siempre somos capaces de descartar una de ellas sin equivocarnos.
Resolución
Pongamos que antes de leer las preguntas directamente hacemos 2 grupos con las respuestas aleatoriamente (un grupo con una pregunta, que será la elegida, y otro grupo con dos).
Posteriormente leemos la pregunta y descartamos la respuestas. Pueden suceder dos situaciones:
- Situación 1: Nuestra elección fue la respuesta incorrecta (1/3 de que suceda). Entonces tenemos que elegir con una probabilidad de 1/2 la pregunta correcta de entre las 2.
- Situación 2: Nuestra elección fue una de las posibles respuestas correctas (2/3 de que suceda)-> En el grupo que hay dos descartamos la 100% incorrecta y nos queda sólo una. ¿Cambiamos la respuesta para aumentar la probabilidad?
Sin tener los conceptos claros uno diría que sí. Al haber descartado una de las respuestas del grupo mayoritario, el 2/3 se concentra en una única respuesta como sucedía en el problema de Monty-Hall… ¿No?
Pues no.
Aquí entra un paso más avanzado. Resulta que al hacer los grupos lo hemos hecho al azar. Por lo tanto, había 1/2 de probabilidades de agrupar la respuesta 100% incorrecta con la realmente correcta y 1/2 de haberla agrupada con la otra incorrecta.
Si calculamos la esperanza matemática puede resultar de 2 maneras pero con el mismo resultado:
1) Jugamos incluso aunque se dé la situación 1: \(E=\frac{1}{3} \cdot \frac{1}{2} + \frac{2}{3} \cdot \frac{1}{2} = \frac{1}{2}\)
2) Jugamos sólo si se da la situación 2: \(E=1 \cdot \frac{1}{2} =\frac{1}{2}\)
Es decir, que al igual que nos indica la lógica, si de 3 respuestas dudamos en 2 de ellas, la probabilidad de acertar al azar es de 1/2 independientemente de la agrupación que hagamos.
Pero… ¿Cuál es la diferencia con el problema de Monty-Hall? ¿Qué se incumple?
La diferencia es que la respuesta incorrecta es incorrecta / “se va a abrir” independientemente de la agrupación que hagamos y la elección que hagamos, siendo realmente una información extra que tenemos previa al juego. La probabilidad surge entonces de agrupar dicha respuesta incorrecta con una u otra. Por lo tanto, sería equivalente al problema de Monty-Hall en el que haya 10 puertas pero 7 de ellas ya estuviesen abiertas previamente mostrando cabras. ¿Para qué meterlas en el juego? ¿Influirían?
Una forma de saber si el planteamiento es adecuado es reducir al absurdo.
Supongamos un examen tipo test en el que haya 10 posibles respuestas, de las cuales sabemos que 8 son 100% incorrectas. En el caso de que agrupemos 1 respuesta que no sabemos en un grupo individual y las otras 9 preguntas en otro grupo de las cuales descartamos 8… ¿Tendríamos un 90% de acertar si elegimos la respuesta del grupo numeroso? Y si tuviésemos un conjunto casi infinito de respuestas de las cuales desconocemos 2 e hiciéramos lo mismo… ¿Tendríamos un 100% de acertar? No tiene sentido.
¿Qué opinas? ¿Conoces otros problemas similares? ¿Te gustó el artículo? ¡Déjame un comentario!




Es la explicación más clara sobre el problema de Monty Hall
Falacia de cabo a rabo. La explicación de 1/3 vs 2/3 es sólo válida en el caso que el concursante pueda hacer 3 apuestas. Con sólo una apuesta sobre dos puertas restantes, la posibilidad de acierto es del 50/100. ¿Por qué nunca se menciona el “pequeño” detalle de que el concursante no puede hacer tres apuestas diferentes? Todos muerden el anzuelo para comprar la moto averiada de la “respuesta anti-intuitiva”. Queda muy bien para reuniones de amigos y divertimentos matemáticos, pero es falacia grosera.
Buenas Pino,
Recientemente publiqué un artículo demostrando con el Teorema de Bayes lo que se expone en este artículo. EL enlace es: https://ingenieriabasica.es/teorema-de-bayes-probabilidad-bayesiana/#Problema_de_Monty-Hall_usando_el_Teorema_de_Bayes
Podría intentar explicártelo con más tranquilidad pero es matemáticas, la prueba está ahí, a ver si te convence 🙂
Gracias por tu respuesta!
Como bien dices en el artículo, las matemáticas nunca fallan… pero hay que aplicarlas bien. Por definición, la probabilidad de un suceso se obtiene como el cociente de los casos favorables entre los casos posibles. Por eso al principio dices que al elegir una puerta tienes 1/3 de probabilidades de acertar: divides 1 (casos favorables), entre 3 (casos posibles).
Pero en el momento en que el presentador abre una de las puertas restantes estás cambiando el problema, porque ahora el número de casos posibles ya es de sólo 2. La probabilidad de acertar con tu elección inicial es de 1/2. Si cambias de puerta, sigues teniendo probabilidad 1/2…
Por eso yo también opino que todo esto es una falacia resultante de aplicar mal las matemáticas.
Buenas Leo;
Si se diese el caso de que al abrir una de las puertas, esta se descarta Y las otras dos puertas se “mezclan”, es decir, se reinicia el problema, estaríamos en el caso que dices; a priori pasa a ser 1/2. Pero como no es el caso, la probabilidad es de 1/3 y 2/3.
Es igual a lo de las apuestas por colores en la ruleta. Si en una ruleta han salido 30 rojos seguidos, ¿qué probabilidad hay de que vuelva a salir rojo? Pues de 1/2 porque son sucesos independientes. Que en el pasado hayan salido muchos rojos no dice nada. Otra cosa muy diferente es decir: qué probabilidad hay de que empiece a jugar y saque 20 rojos seguidos? En este caso la probabilidad es bajísima, porque estás obligando a que sean sucesos dependientes.
Espero que con este último ejemplo lo hayas entendido
Buenas luisyep:
Tan sólo con aplicar la definición de probabilidad, como te he indicado, tendrías que haber visto tu error, pero reconozco que es un problema planteado de forma que te hace “picar”.
Si te parece, centrémonos en la esencia de lo que se plantea:
1. Tenemos tres puertas, una con un coche, y dos con cabras.
2. Elijas lo que elijas, el presentador va a abrir una puerta con una de las cabras.
3. Es decir, tu elección SIEMPRE se va a estar entre coger una puerta con una cabra o una puerta con un coche. No hay más posibilidades. Probabilidad de ganar: 1/2 (1 caso favorable entre dos posibles).
En cuanto a tu primer argumento: Resulta que al abrir una de las puertas ¡la estamos descartando!, porque estamos quitando una cabra siempre. La cosa sería muy distinta si el presentador abriera la puerta al azar, pero entonces a lo mejor no salía una cabra…
En cuanto a tu segundo argumento: No es el mismo caso, así que no explica nada relacionado con el problema de Monty Hall. Eso sí, podríamos hacerlo parecido si vamos quitando una casilla negra cada vez que apostamos a rojo. ¿Seguirías diciendo entonces que la probabilidad de sacar rojo cada vez es 1/2, o verías que estamos tratando un problema distinto cada vez, al igual que hemos hecho al quitar una cabra?
Un saludo
Hola Leo;
Antes de nada te agradezco enormemente que te hayas tomado la molestia no sólo de redactar un mensaje tan largo sino de volver a la página para ver mis respuestas y tal. De verdad, gracias.
A lo que me respondes, pues no sé qué decirte. No es un tema fácil ni de explicar ni de comprender. Yo he hecho lo que he podido pero es muy muy difícil cambiar la opinión de alguien.
Yo creo saber de matemáticas y no sólo mi escaso conocimiento me avala sino cientos de webs que hablan sobre este problema y dan como solución la que expongo en el artículo. Lamento no ser capaz de convencerte con mis argumentos.
Un saludo!
Hola, luisyep:
Yo también creo que es muy difícil hacer cambiar de opinión a alguien cuando está tan convencido de su postura, pero creo que no habría podido expresarlo de una forma tan elegante como has hecho tú.
Muchas gracias!
me import5a una raja ojala expliquen mejor y mas resumido pq me da paja leer todo esto
Para quien argumenta a favor del 50%, propongo una manera, creo que sencilla, de ver que en realidad es 2/3 cambiando de puerta.
Hay que darse cuenta de que en realidad no hay ningún “cambio” en la situación del problema en ningún momento, se puede plantear en conjunto a priori. Las premisas son:
1) Vas a elegir una de las tres puertas
2) El presentador va a abrir, de entre las otras dos, una puerta sin premio
3) Vas a poder cambiar tu elección inicial por la puerta restante
Sabiendo esto, la estrategia de cambiar o no cambiar de puerta se puede elegir también a priori.
Elijo que voy a cambiar de puerta. La pregunta es, entonces, ¿en cuántos de los posibles casos me acabaré llevando el premio? O lo que es lo mismo, ¿en cuántos casos no me lo llevaré?
La única forma de no llevarme el premio es que mi elección inicial sea la puerta del premio (1/3). En los otros dos casos, cuando mi elección inicial es una puerta sin premio (2/3), al cambiar de puerta me voy a llevar el premio.
Otro modo de convencerse es hacer el experimento con las dos estrategias: toma tres cartas, elige cuál de las tres será el premio, y pide a alguien que haga el papel del presentador. Juega 100 veces con la estrategia de no cambiar de puerta, y juega otras 100 veces con la estrategia de cambiar. Apunta en cada caso cuántas de las 100 veces te llevas el premio, y compara resultados.
Saludos!