Artículo anterior:
En este artículo desarrollaremos el concepto de deformación y desplazamiento, indicando cómo se produce el movimiento de los puntos de un sólido deformable tras sufrir un esfuerzo.
En el libro de París se encuentra un desarrollo alternativo, a mi parecer, más lioso y difícil de entender al que se expondrá en este artículo. Obviamente el concepto es el mismo.
Tensor de deformación
Una vez definidos los esfuerzos en un sólido deformable, vamos a analizar cómo se deforma. Es completamente intuitivo pensar que cuando aplicamos una presión sobre un cuerpo, este va a tender a deformarse. Sería como pensar en una goma elástica, pero más bien como si los átomos del cuerpo estuvieran unidos entre sí con gomas elásticas de forma que todo el cuerpo se deforma en conjunto y de forma continua.
Como hemos dicho, cuando un cuerpo elástico se encuentra bajo la acción de esfuerzos, este cambia su forma. Una forma de analizar el problema es observar la relación entre la posición de los puntos antes y después de que la deformación tenga lugar.
Definiendo la posición inicial como:
\(\vec{x}= x\vec{i} + y\vec{j} + z \vec{k}\)Y definiendo las componentes de la posición final con funciones escalares:
\(\vec{X} = \left \{ \begin{matrix} X=\phi_{x}(x,y,z)= x + u_{x}(x,y,z) \\ Y=\phi_{y}(x,y,z)= y + u_{y}(x,y,z) \\ Z=\phi_{z}(x,y,z)= z + u_{z}(x,y,z) \end{matrix} \right.\)Dada una distancia orientada infinitesimal del cuerpo indeformado \(\delta\vec{ x}\), podemos definir el gradiente de deformación como el operador que nos da la distancia \(\delta\vec{ X} \) después de la deformación
\(\delta \vec{X} = [F] * \delta \vec{x}\)
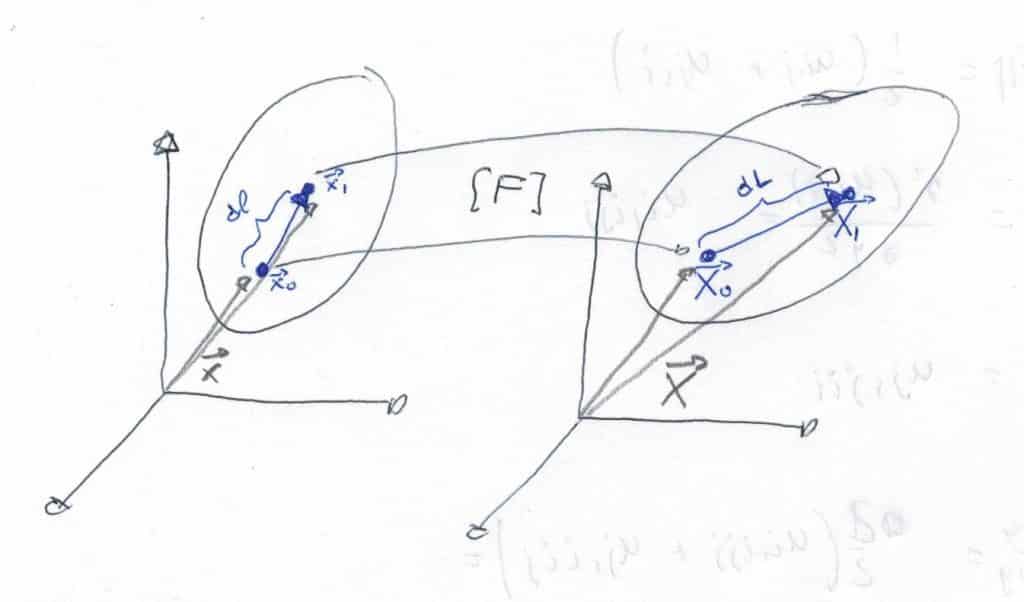
De forma que:
\([F] = \frac{\delta \vec{X}}{\delta \vec{x}} = \left [ \frac{\partial \phi_{i}}{\partial x_{j}} \right ] = [I] + \frac{\partial u_{i}}{\partial x_{j}} = \left [ \begin{matrix} 1 + \frac{\partial u_{x}}{\partial x} & \frac{\partial u_{x}}{\partial y} & \frac{\partial u_{x}}{\partial z} \\ \\ \frac{\partial u_{y}}{\partial x} & 1 + \frac{\partial u_{y}}{\partial y} & \frac{\partial u_{y}}{\partial z} \\ \\ \frac{\partial u_{z}}{\partial x} & \frac{\partial u_{z}}{\partial y} & 1 + \frac{\partial u_{z}}{\partial z} \end{matrix}\right ]\)
El siguiente paso es definir arbitrariamente el valor de la deformación directa en una dirección como:
\(\epsilon = \frac{1}{2} \frac{dL^{2} – dl^{2}}{dl^{2}}, \ con \ \left \{ \begin{matrix} dL^{2} = \delta\vec{X}^{T}*\delta\vec{X} \\ dl^{2} = \delta\vec{x}^{T}*\delta\vec{x} \end{matrix} \right.\)
(Para hacer producto escalar entre vectores debemos expresar el primero como «traspuesto» de manera que se obtiene una matriz 1×1)
Expresamos el valor de \(\delta \vec{X}\) con la definición del gradiente de deformación:
\(\delta\vec{X}^{T}*\delta\vec{X} = ([F] * \delta \vec{x})^{T}([F] * \delta \vec{x})=\delta\vec{x}^{T}[F]^{T}[F]\delta\vec{x}\)
Introduciendo en \(\epsilon\):
\(\epsilon = \frac{1}{2}\frac{\delta\vec{x}^{T}[F]^{T}[F]\delta\vec{x} \ \ – \ \ \delta\vec{x}^{T}[I]\delta\vec{x} }{\delta\vec{x}^{T}\delta\vec{x}} = \frac{1}{2}\frac{\delta\vec{x}^{T}([F]^{T}[F] – [I]) \delta\vec{x} }{\delta\vec{x}^{T}\delta\vec{x}} \)
Definiendo \([E] = \frac{1}{2} ([F]^{T}[F] – [I])\) el tensor de deformaciones de Green-Lagrange->
\(\epsilon = \frac{2}{2} \frac{\delta\vec{x}^{T}[E] \delta\vec{x}}{\delta\vec{x}^{T}\delta\vec{x}} \rightarrow \boxed{\epsilon = \vec{N}^{T} * [E] * \vec{N}}\)
Desarrollando el tensor de deformaciones de Green-Lagrange:
\([E] = E_{ij} = \frac{1}{2} (F_{ki}F_{kj} – \delta_{ij}) \rightarrow E_{ij}=\frac{1}{2} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}} +\frac{\partial u_{k}}{\partial x_{i} \frac{\partial u_{k}}{\partial x_{j}}}) \approx \frac{1}{2} (\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}}) \)Asumiendo deformaciones pequeñas, de forma que podemos despreciar el término al cuadrado de la deformación, obtenemos la forma del tensor de pequeñas deformaciones \([\epsilon]= \boxed{\epsilon_{ij} = \frac{1}{2} \left(\frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}}\right )}\)
\([\epsilon]=\left [ \begin{matrix} \frac{\partial u_{x}}{\partial x} & \frac{1}{2}(\frac{\partial u_{x}}{\partial y}+\frac{\partial u_{y}}{\partial x}) & \frac{1}{2}(\frac{\partial u_{x}}{\partial z}+\frac{\partial u_{z}}{\partial x}) \\ \\ \frac{1}{2}(\frac{\partial u_{x}}{\partial y}+\frac{\partial u_{y}}{\partial x}) & \frac{\partial u_{y}}{\partial y} & \frac{1}{2}(\frac{\partial u_{y}}{\partial z}+\frac{\partial u_{z}}{\partial y}) \\ \\ \frac{1}{2}(\frac{\partial u_{x}}{\partial z}+\frac{\partial u_{z}}{\partial x}) & \frac{1}{2}(\frac{\partial u_{y}}{\partial z}+\frac{\partial u_{z}}{\partial y}) & \frac{\partial u_{z}}{\partial z} \end{matrix} \right ] \)
El cual observamos que es simétrico.
Gradiente de desplazamientos
En vez de centrarnos en la deformación directa en una dirección, vamos a observar qué sucede con los puntos que se desplazan. Partiendo de la posición inicial y obteniendo una linealización de los desplazamientos, la posición final de los puntos es:
\(\vec{X} = \begin{cases} X = x + \frac{\partial u_{x}(x,y,z)}{\partial x} dx + \frac{\partial u_{x}(x,y,z)}{\partial y} dy + \frac{\partial u_{x}(x,y,z)}{\partial z} dz \\ Y = y + \frac{\partial u_{y}(x,y,z)}{\partial x} dx + \frac{\partial u_{y}(x,y,z)}{\partial y} dy + \frac{\partial u_{y}(x,y,z)}{\partial z} dz \\ Z = z + \frac{\partial u_{z}(x,y,z)}{\partial x} dx + \frac{\partial u_{z}(x,y,z)}{\partial y} dy + \frac{\partial u_{z}(x,y,z)}{\partial z} dz \end{cases}\)O, lo que es lo mismo:
\(\boxed{\vec{X}=\vec{x} + [M] * d\vec{r}}\)
Siendo \([M]=grad\{\vec{u}\}=\left [ \begin{matrix} \frac{\partial u_{x}}{\partial x} & \frac{\partial u_{x}}{\partial y} & \frac{\partial u_{x}}{\partial z} \\ \\ \frac{\partial u_{y}}{\partial x} & \frac{\partial u_{y}}{\partial y} & \frac{\partial u_{y}}{\partial z} \\ \\ \frac{\partial u_{z}}{\partial x} & \frac{\partial u_{z}}{\partial y} & \frac{\partial u_{z}}{\partial z} \end{matrix} \right ]\)
Denominamos \([M]\) al gradiente de desplazamientos, el cual expresa cómo los puntos de un cuerpo se desplazan.
Significado del gradiente de desplazamientos en un cuadrado con su deformada
Vamos a analizar cómo afecta el gradiente de desplazamientos a un cuadrado (Como lo deforma) viendo explícitamente el significado de cada una de las componentes de la matriz.
Deformación lineal (Diagonal de la matriz)
Se produce una deformación «en la misma dirección de la derivada». Está asociado a un cambio de volumen o deformación normal.
El gradiente representa la evolución del desplazamiento a medida que recorremos una distancia (La variable que deriva). En el primer caso, el desplazamiento hacia el eje positivo x aumenta a medida que aumenta x, de forma que tiende a alargarse. En el segundo caso, el desplazamiento hacia arriba disminuye a medida que aumenta y, de forma que tras «integrar» las deformaciones se obtiene un rectángulo más corto.
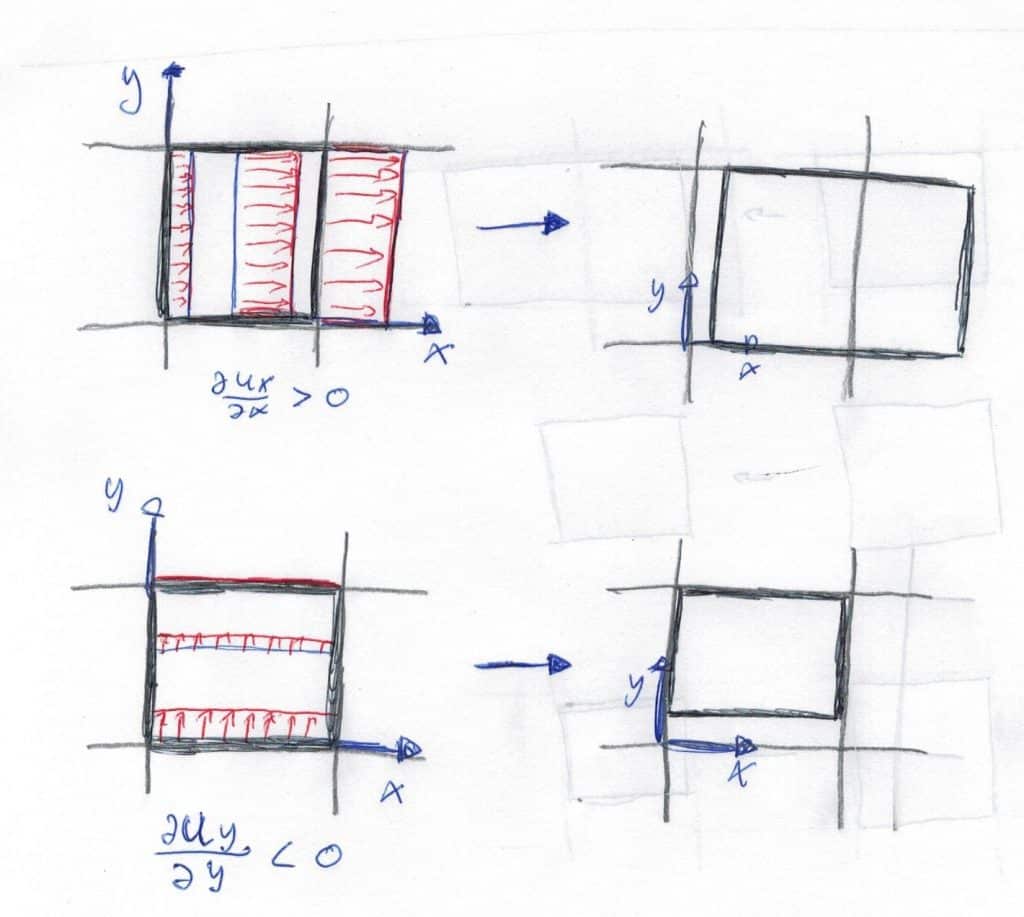
A la izquierda observamos el gradiente de desplazamientos sobre el cuadrado indeformado y a la derecha el resultado.
Deformación angular (Tangencial simétrico + rotación rígida)
Se produce una deformación angular, la cual se relaciona con una deformación tangencial simétrica y una rotación como sólido rígido. Se debe a las componentes de fuera de la diagonal las cuales representan una evolución del desplazamiento en una dirección diferente hacia la cual se deriva.
Es una deformación tangencial, y como tal, no produce una variación de volumen (Como veremos más adelante), sino que produce únicamente un cambio de forma.
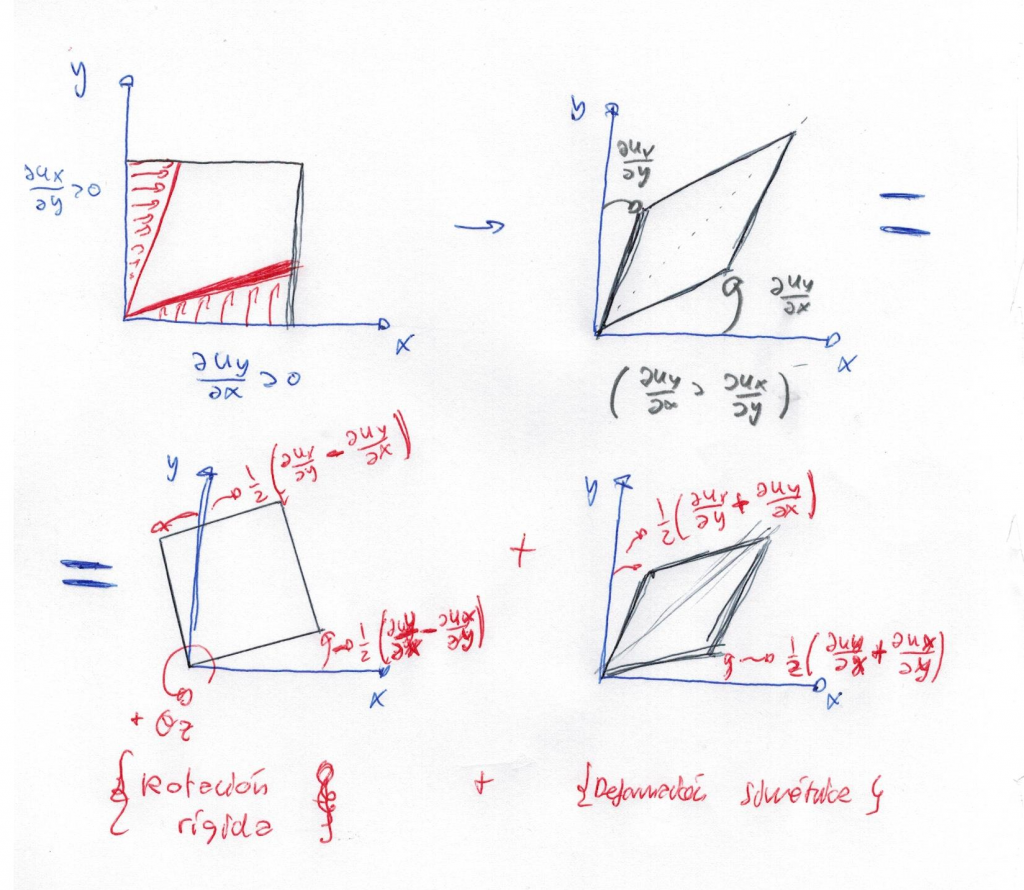
Observamos que podemos rotar y deformar simétricamente o deformar simétricamente y luego rotar. Si sumamos ambos efectos obtenemos la resultante esperada.
Desarrollo del gradiente de desplazamientos
Acabamos de ver con las deformaciones angulares que podemos expresar el gradiente de desplazamientos como una parte que rota y otra que se deforma simétricamente:
\([M]=\underbrace{\frac{1}{2} ([M] + [M]^{T})}_{[\epsilon]: \ Tensor \ de \ pequeñas \ deformaciones} + \underbrace{\frac{1}{2} ([M] – [M]^{T})}_{[\theta]: \ Tensor \ de \ rotacion}\)Donde \([\theta]\) lo definimos como el tensor de rotación:
\([\theta]= \left [ \begin{matrix} 0 & \frac{1}{2}(\frac{\partial u_{x}}{\partial y}-\frac{\partial u_{y}}{\partial x}) & \frac{1}{2}(\frac{\partial u_{x}}{\partial z}-\frac{\partial u_{z}}{\partial x}) \\ \\ \frac{1}{2}(\frac{\partial u_{y}}{\partial x}-\frac{\partial u_{x}}{\partial y}) & 0 & \frac{1}{2}(\frac{\partial u_{y}}{\partial z}-\frac{\partial u_{z}}{\partial y}) \\ \\ \frac{1}{2}(\frac{\partial u_{z}}{\partial x}-\frac{\partial u_{x}}{\partial z}) & \frac{1}{2}(\frac{\partial u_{z}}{\partial y}-\frac{\partial u_{y}}{\partial z}) & 0 \end{matrix} \right ] = \left [ \begin{matrix} 0 & -\theta_{z} & \theta_{y} \\ \theta_{z} & 0 & -\theta_{x} \\ -\theta_{y} & \theta_{x} & 0 \end{matrix} \right ] \)El cual es una matriz antisimétrica. Los signos positivos y negativos se indican en base a una rotación positiva (Eje de rotación perpendicular al folio y va en sentido antihorario) o negativa (Mismo eje de giro pero en sentido horario) para valores positivos de las derivadas.
Descomponiendo el gradiente de desplazamiento en el tensor de pequeñas deformaciones y el tensor de rotación podemos expresar el movimiento de los puntos como:
\(\vec{X}=\underbrace{\vec{x} + [\theta]*d\vec{r}}_{Movimiento \ rigido} + \underbrace{[\epsilon]*d\vec{r}}_{Deformacion}\)
Por una parte, en la asignatura de Mecánica se estudia el comportamiento del sólido rígido y sus complejos movimientos asumiendo que no se deforma. Por otra parte, en la Teoría de la Elasticidad se estudia el sólido deformable pero exclusivamente sus deformaciones. Un paso más avanzado es el de unir ambas teorías y estudiar el comportamiento absoluto de un cuerpo que se mueve con cierta velocidad y al mismo tiempo se deforma, siendo el comportamiento real de los sólidos.
Es por ello que, como en este ámbito de estudio nos centramos en las tensiones y las deformaciones en un cuerpo, ignoramos la primera parte de los desplazamientos suponiendo que el sólido se encuentra en reposo al aplicar/cesar el esfuerzo y que no se acelera en ningún momento, de forma que existe un desplazamiento de los puntos debido exclusivamente a la deformación y el cuerpo no adquiere velocidad, a diferencia de como se estudia en la mecánica del sólido rígido.
Observamos que hemos obtenido una misma definición y forma del tensor de pequeñas deformaciones empleando dos caminos; En el primero, tras definir de forma arbitraria el concepto de deformación directa y a partir de ello obtener la forma del tensor asumiendo pequeñas deformaciones. El segundo camino ha sido el de linealizar los desplazamientos y expresar el gradiente de desplazamientos en una parte de sólido rígido y en otra parte debida a las deformaciones.
Desarrollo del tensor de pequeñas deformaciones
\([\epsilon] = \begin{bmatrix} \epsilon_{xx} & \frac{\gamma_{xy}}{2} & \frac{\gamma_{xz}}{2} \\ \frac{\gamma_{xy}}{2} & \epsilon_{yy} & \frac{\gamma_{yz}}{2} \\ \frac{\gamma_{xz}}{2} & \frac{\gamma_{yz}}{2} & \epsilon_{zz} \end{bmatrix}, \quad \text{con} \quad \begin{cases} \epsilon_{ii} = \frac{\partial u_{i}}{\partial x_{i}} \\ \gamma_{ij} = \gamma_{ji} = \frac{\partial u_{i}}{\partial x_{j}} + \frac{\partial u_{j}}{\partial x_{i}} = 2 \epsilon_{ij} \end{cases}\)
Direcciones principales
Al igual que con los esfuerzos, también podemos definir direcciones principales donde las deformaciones se alinean directamente con la dirección, de forma que no hay deformaciones tangenciales en dichas direcciones.
\( [\epsilon]*\vec{n} = e*\vec{n} \ \ \ \iff \ \ \ ([\epsilon]-e[I])*\vec{n}=0 \rightarrow e^{3} – I_{1}e^{2} + I_{2} e – I_{3}=0\)Con:
\(\left\{ \begin{matrix} I_{1} = \operatorname{tr}([\epsilon]) = \epsilon_{11} + \epsilon_{22} + \epsilon_{33} = e_{I} + e_{II} + e_{III} = \epsilon_{\text{vol}} \\ \\ I_{2} = \epsilon_{11} \epsilon_{22} + \epsilon_{11} \epsilon_{33} + \epsilon_{22} \epsilon_{33} – \epsilon_{12}^{2} – \epsilon_{23}^{2} – \epsilon_{13}^{2} \\ \\ I_{3} = \operatorname{Det}([\epsilon]) \end{matrix} \right. \)El procedimiento y sus resultados es idéntico al seguido con las tensiones.
Deformación volumétrica
En un sistema de direcciones principales es fácil demostrar que:
\(\left\{ \begin{matrix} dV_{0} = dx_{I} dx_{II} dx_{III} \\ \\ dV = dV_{0} + (e_{I} dx_{I}) dx_{II} dx_{III} + (e_{II} dx_{II}) dx_{I} dx_{III} + (e_{III} dx_{III}) dx_{I} dx_{II} \\ = (1 + e_{I} + e_{II} + e_{III}) dV_{0} \end{matrix} \right.\)
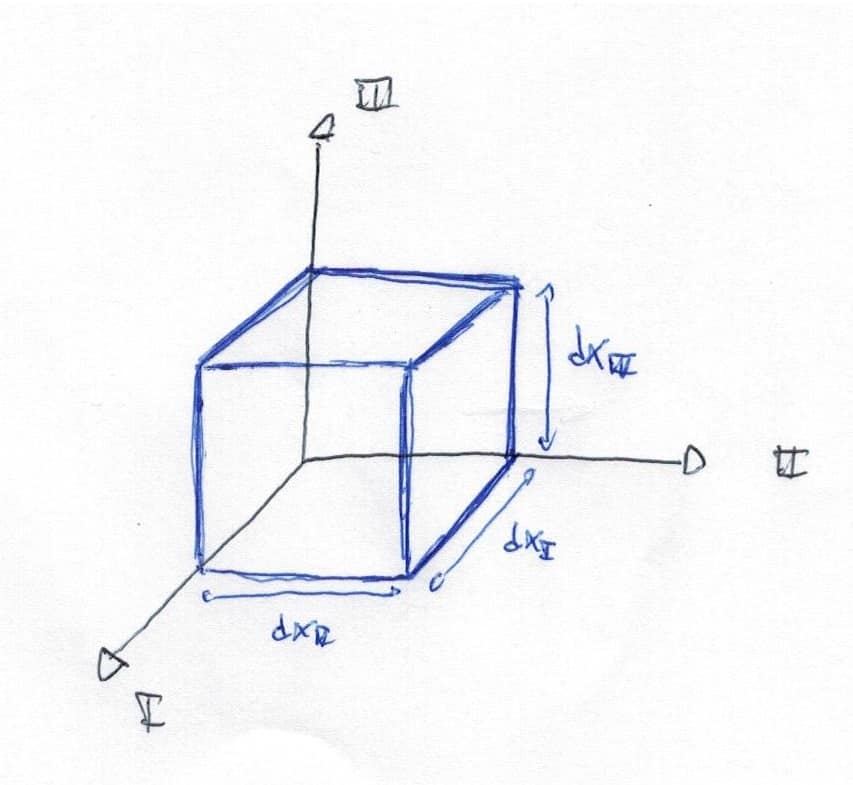
Definiendo la deformación volumétrica como:
\(\epsilon_{vol}=\frac{dV-dV_{0}}{dV_{0}} = e_{I}+e_{II}+e_{III} = tr([\epsilon]) = \boxed{ \epsilon_{xx} + \epsilon_{yy} +\epsilon_{zz} = \epsilon_{vol}}\)
De esta forma demostramos que el cambio de volumen se asocia y depende exclusivamente de las deformaciones normales.
Tensor esférico y desviador
Siguiendo un proceso análogo al seguido con el tensor de tensiones:
\([\epsilon] = [\epsilon_{esf}] + [\epsilon_{desv}] = \underbrace{\dfrac{\epsilon_{vol}}{3}[I]}_{[\epsilon_{esf}]} + \underbrace{([\epsilon] – \dfrac{\epsilon_{vol}}{3}[I])}_{[\epsilon_{desv}]}\)
Ecuaciones de compatibilidad
Si conocemos el campo de desplazamientos \(\vec{u}\) de un sólido de forma continua y univaluada, entonces podemos expresar el tensor de pequeñas deformaciones como \(\epsilon_{ij} = \frac{1}{2} (u_{i,j} + u_{j,i})\) y obtener instantáneamente una forma válida del tensor.
Sin embargo, no cualquier forma del tensor es válida para generar un campo válido de desplazamientos. Las componentes del tensor deben de verificar una serie de ecuaciones para demostrar la validez y congruencia entre ellas de forma que no se produzcan desplazamientos absurdos.
Estas ecuaciones se obtienen tras derivar dos veces la definición de las componentes del tensor de pequeñas deformaciones en función del campo de desplazamientos y comprobar la equivalencia entre los valores.
Se obtiene un total de 6 ecuaciones, de las cuales sólo 3 son linealmente independientes:
\(\begin{matrix} 1) & \dfrac{\partial^{2} \epsilon_{xx}}{\partial y^{2}} + \dfrac{\partial^{2} \epsilon_{yy}}{\partial x^{2}} &= &2*\dfrac{\partial^{2} \epsilon_{xy}}{\partial x \partial y} \\ \\ 2) & \dfrac{\partial^{2} \epsilon_{xx}}{\partial z^{2}} + \dfrac{\partial^{2} \epsilon_{zz}}{\partial x^{2}} &=& 2*\dfrac{\partial^{2} \epsilon_{xz}}{\partial x \partial z} \\ \\ 3) & \dfrac{\partial^{2} \epsilon_{yy}}{\partial z^{2}} + \dfrac{\partial^{2} \epsilon_{zz}}{\partial y^{2}} &= &2*\dfrac{\partial^{2} \epsilon_{yz}}{\partial y \partial z} \\ \\ 4) & \dfrac{\partial^{2} \epsilon_{xy}}{\partial x \partial z} + \dfrac{\partial^{2} \epsilon_{xz}}{\partial x \partial y} &=& \dfrac{\partial^{2} \epsilon_{xx}}{\partial y \partial z} +\dfrac{\partial^{2} \epsilon_{yz}}{\partial x^{2}} \\ \\ 5) & \dfrac{\partial^{2} \epsilon_{xy}}{\partial y \partial z} + \dfrac{\partial^{2} \epsilon_{yz}}{\partial x \partial y} &= &\dfrac{\partial^{2} \epsilon_{yy}}{\partial x \partial z} +\dfrac{\partial^{2} \epsilon_{xz}}{\partial y^{2}} \\ \\ 6) & \dfrac{\partial^{2} \epsilon_{xz}}{\partial y \partial z} + \dfrac{\partial^{2} \epsilon_{yz}}{\partial x \partial z} &= & \dfrac{\partial^{2} \epsilon_{zz}}{\partial x \partial y} +\dfrac{\partial^{2} \epsilon_{xy}}{\partial z^{2}} \end{matrix}\)
Por ejemplo, en la primera ecuación:
\(1) \left \{ \begin{matrix} \dfrac{\partial^{2} \epsilon_{xx}}{\partial y^{2}} & = & \dfrac{\partial(u_{x,x})}{\partial y^{2}} & = & u_{x,xyy} \\ \\ \dfrac{\partial^{2} \epsilon_{yy}}{\partial x^{2}} & = & \dfrac{\partial(u_{y,y})}{\partial x^{2}} & = & u_{y,yxx} \\ \\ 2 \cdot \dfrac{\partial^{2} \epsilon_{xy}}{\partial x \partial y} & = & \dfrac{2}{2} (u_{x,yxy} + u_{y,xxy}) & = & u_{x,xyy} + u_{y,yxx} \end{matrix} \right. \rightarrow \dfrac{\partial^{2} \epsilon_{xx}}{\partial y^{2}} + \dfrac{\partial^{2} \epsilon_{yy}}{\partial x^{2}} = 2 \cdot \dfrac{\partial^{2} \epsilon_{xy}}{\partial x \partial y}\)Lo mismo sucede con el resto de ecuaciones, y como observamos no es más que una serie de ecuaciones que verifican la validez de las componentes del tensor. Por lo tanto, cumplir estas ecuaciones es una condición necesaria pero no suficiente (Con estas ecuaciones no obtenemos la forma del tensor) para definir un tensor de deformaciones válido.
Observamos que si las componentes del tensor no tienen derivadas segundas, automáticamente cualquier forma del tensor de tensiones es válida (Compatible) ya que se verifican las ecuaciones automáticamente.
Es decir:
- Dado un campo de desplazamientos continuo y univaluado -> Podemos definir con exactitud un tensor de pequeñas deformaciones completamente válido.
- Dado un tensor de pequeñas deformaciones -> Para verificar su validez y poder obtener el campo de desplazamientos, las componentes de dicho tensor deben de verificar las ecuaciones de compatibilidad.
Artículo siguiente:

![[Elasticidad y Resistencia de Materiales] Teoría de la Elasticidad Portada-elasticidad-alta](https://ingenieriabasica.es/wp-content/uploads/2020/07/Portada-elasticidad-alta-200x136.jpg)