Artículo anterior:
En los artículos anteriores hemos definido y desarrollado el concepto de tensión y deformación. Sin embargo, no hemos hablado de la relación directa existente entre ambos conceptos. En este artículo obtendremos dicha relación para un cuerpo que se deforma al someterse a esfuerzos.
Al igual que en el artículo anterior, se emplea un desarrollo alternativo al que se sigue de forma principal en el libro de París.
A la hora de representar la relación entre deformaciones y tensiones, emplearemos la notación de Voigt, la cual nos permite expresar tensores simétricos en una forma reducida. Por este motivo, y por el posterior desarrollo de los esfuerzos tangenciales, las deformaciones tangenciales se escriben en la versión de \(\gamma\).
El ensayo de tracción
El ensayo de tracción consiste en aplicar un esfuerzo de tracción creciente sobre una probeta hasta que se produzca su rotura. El objetivo de dicho ensayo es analizar cómo se ha ido alargando la probeta a medida que ha aumentado la fuerza. Es decir, obtener su curva de tensión-deformación.
Directamente tenemos la fuerza que genera la máquina y la distancia que mide una regla. Para analizar la tensión y la deformación de la probeta hay que hacer:
\(\left\{ \begin{matrix} \sigma = \frac{F}{A_{0}} & \text{Tensión ingenieril} & , & \{\sigma_{\text{real}} = \frac{F}{A}\} \\ \\ \epsilon = \frac{\Delta L}{L_{0}} & \text{Deformación ingenieril} & , & \{\epsilon_{\text{real}} = \ln\left(\frac{L_{0} + \Delta L}{L_{0}}\right)\} \end{matrix} \right.\)Siendo \(A_{0}\) la sección de la probeta y \(L_{0}\) su longitud inicial.
- En realidad, a medida que se alarga la probeta, la sección disminuye, de forma que no deberíamos de considerarla constante, sino que sería función de la elongación.
- En el caso de la deformación, se debería de expresar como logaritmo en caso de tener deformaciones acumuladas, de forma que se expresase correctamente la deformación total.
Sin embargo, para simplificar el estudio, se considera constante la sección y no tenemos en cuenta deformaciones acumuladas.
Curva de tensión-deformación
La curva de tensión-deformación es la curva experimental que marca la relación entre tensión y deformación que sufre una probeta en el ensayo de tracción.
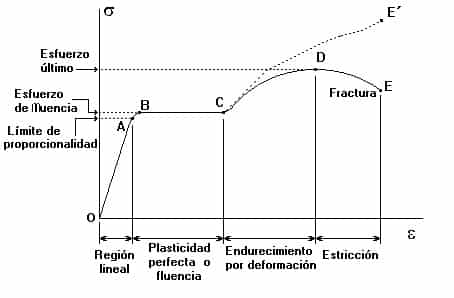
En la curva de tensión-deformación observamos varios tramos:
- O-A: Comportamiento elástico lineal, con pendiente de la recta igual al módulo de Young E
- A-B: Comportamiento elástico no lineal.
- B-C: Tramo de “creep” o fluencia. El material comienza a adquirir deformaciones permanentes y apenas es necesario aumentar la fuerza para seguir aumentando la deformación.
- C-D: Tramo de endurecimiento por deformación. El material sigue adquiriendo deformaciones plásticas permanentes y es necesario aumentar la fuerza para seguir aumentando la deformación.
- D-E: Se produce la estricción de la probeta (Disminuye su sección transversal) en una zona localizada y posteriormente se produce la rotura en dicha zona. Observamos que en este tramo existe una gran diferencia entre la tensión ingenierística y la real ya que la sección disminuye notablemente.
A partir del punto B, la deformación deja de ser elástica, de forma que al cesar el esfuerzo el material no recuperará la forma original. Para más detalles acerca de cómo se recupera y cómo se vuelve a deformar un material ya deformado, consultad el libro de París.
Observamos que durante el tramo elástico, la relación entre \(\sigma\) y \(\epsilon\) es lineal, dado por el módulo de Young \(E\)
\(\boxed{E := \dfrac{\sigma}{ \epsilon}} \ \ \) en el tramo elástico, y su valor depende de la rigidez del material.
Para materiales con mayor módulo de Young, la fuerza necesaria para producir la misma deformación es mayor, de forma que a mayor módulo, mayor es la rigidez del material.
A medida que la probeta adquiere deformaciones permanentes, comienza a disminuir su sección. La relación entre la deformación longitudinal y transversal se expresa mediante el coeficiente de Poisson \(\nu\)
\(\nu := |\dfrac{\epsilon_{t}}{\epsilon_{l}}| \rightarrow \epsilon_{trans} = – \nu * \epsilon_{l} = \boxed{-\nu * \dfrac{\sigma}{E} =\epsilon_{trans}} \)Ley de Hooke generalizada para materiales isotrópicos
En un sólido deformable isotrópico (Su comportamiento es el mismo en todas las direcciones), la elongación es proporcional a la fuerza durante el tramo de comportamiento lineal, tal y como sucedería en un muelle. Es por ello que se llama Ley de Hooke generalizada.
La constante de proporcionalidad, como imaginamos, viene dada por el módulo de Young,
\( \epsilon = \dfrac{\sigma}{E} = \dfrac{\bigtriangleup L}{L} = \dfrac{F}{A*E} \rightarrow \boxed{ \bigtriangleup L = \dfrac{F}{A*E}*L}\)
Materiales Hiperelásticos
Un material hiperelástico es un material elástico al cual se le pueden relacionar los esfuerzos y las deformaciones mediante un potencial elástico. La gran mayoría de materiales elásticos son a su vez hiperelásticos.
Podemos expresar la densidad de energía de deformación como:
\(U(\epsilon_{ij}) = \int_{0}^{\epsilon_{ij}} \sigma_{ij}(\epsilon_{kk}) d\epsilon_{ij} \rightarrow \sigma_{ij} = \frac{dU(\epsilon_{ij})}{d\epsilon_{ij}}\)Definiendo un tensor de rigidez podemos explicitar la dependencia de \([\sigma]\) con \([\epsilon]\). Definimos el tensor de rigidez \([[D]]\) como un tensor cuádruple (81 componentes) que relaciona \([\sigma]\) y \([\epsilon]\) como \(\boxed{[\sigma] = [[D]] [\epsilon] }\)
De esta forma:
\(U = \int_{0}^{\epsilon_{ij}} \sigma_{ij}(\epsilon_{kk}) d\epsilon_{ij} = \int_{0}^{\epsilon_{ij}} D_{ijkk} *\epsilon_{kk} d\epsilon_{ij} = \boxed { \frac{1}{2} \sigma*\epsilon = U}\)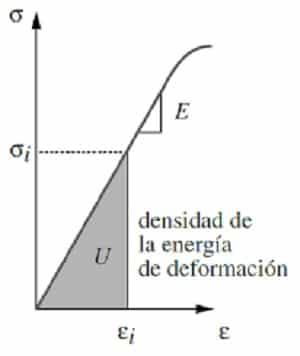
Que encuentra cierta similitud con la energía de deformación de un muelle. Recordamos que este valor es un valor de densidad de energía por unidad de volumen, es decir, \(\dfrac{J}{m^{3}}\)
Debido a términos simétricos y redundantes, de los 81 componentes sólo 21 son únicos. Además, podemos definir la inversa de la matriz de rigidez, y de esta forma expresar las deformaciones en función de los esfuerzos, una forma más cómoda para poder definir los términos de la matriz.
\([\epsilon] = [[C]] * [\sigma] \ , \ con \ [[C]] = [[D]]^{-1}\)
Para representar la relación entre los tensores de deformación y tensión así como el tensor cuádruple de rigidez, empleamos una forma reducida denominada notación de Voigt. De esta manera, se ignoran los términos simétricos y es posible expresar todos los términos imprescindibles sin problemas.
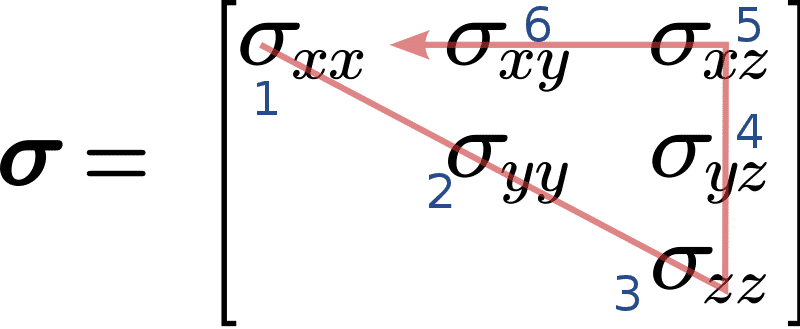
Como anunciado en la introducción, se emplea \(\gamma\) en vez de \(\epsilon\) porque son términos duplicados del tensor, y si queremos hacer el producto entre tensores en forma de voigt automáticamente aparecen duplicadas las deformaciones tangenciales y el producto puede hacerse como si fuera un simple producto escalar de vectores 1×6.
\(\left [ \begin{matrix} \epsilon_{xx} \\ \epsilon_{yy} \\ \epsilon_{zz} \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{matrix} \right ] = \underbrace{\left [ \begin{matrix} C_{11} & C_{12} & C_{13} & C_{14} & C_{15} & C_{16}\\
C_{12} & C_{22} & C_{23} & C_{24} & C_{25} & C_{26}\\
C_{13} &C_{23} & C_{33} & C_{34} & C_{35} & C_{36}\\
C_{14} &C_{24} & C_{34}& C_{44} & C_{45} & C_{46} \\
C_{15} & C_{25} & C_{35} & C_{45} & C_{55} & C_{56} \\ C_{16} & C_{26} & C_{36} & C_{46} & C_{56} & C_{66} \end{matrix} \right ]}_{Simetrica \ \rightarrow \ 21 \ componentes \ unicas} * \left [ \begin{matrix}
\sigma_{xx} \\ \sigma_{yy} \\ \sigma_{zz} \\ \sigma_{yz} \\ \sigma_{xz} \\ \sigma_{xy} \end{matrix} \right ] \)
Este tensor, que es el inverso del tensor de rigidez, se denomina el tensor de flexibilidad.
Ley de comportamiento para materiales elasticos, lineales e isotrópicos
Vamos a desarrollar las constantes de este tensor cuádruple para el caso de un material elástico, lineal e isotrópico.
- Como es lineal, podemos aplicar el principio de superposición y así desarrollar los valores de deformaciones que se produzcan de forma aislada para luego sumarlas y que actúen en conjunto.
- Si el material es isotrópico, la relación entre esfuerzo y deformación será la misma en todas las direcciones, pudiendo extrapolar un resultado al resto de direcciones.
Relación entre el tipo de esfuerzo y el tipo de deformación
Empleando un método de reducción al absurdo vamos a demostrar que esfuerzos normales NO pueden producir deformaciones tangenciales, y que esfuerzos tangenciales producen EXCLUSIVAMENTE deformaciones en la misma dirección de aplicación.
Tomaremos un cubo (Isotrópico, lineal y elástico) de referencia al cual le aplicaremos esfuerzos e hipotizaremos una deformación. Tras aplicar el mismo esfuerzo una vez rotado (Es isotrópico, la deformación debería de ser la misma), veremos que esa deformación no es posible.
Esfuerzos normales
Vamos a suponer que un esfuerzo de tracción se realiza en las caras laterales y se produce una deformación tangencial \(\epsilon_{yz} > 0 \).
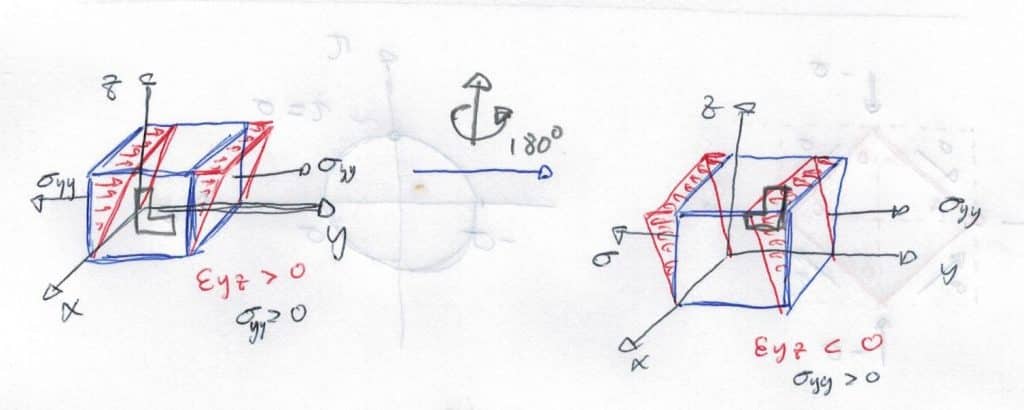
Tras girar el cubo alrededor del eje z 180º y aplicar el mismo esfuerzo, observamos que obtendríamos un \(\epsilon_{yz} < 0 \) para el mismo esfuerzo, resultando una deformación incompatible con nuestras hipótesis al no ser lineal. Haciendo el mismo ejercicio para el resto de direcciones, demostramos que esfuerzos normales NO pueden producir deformaciones tangenciales.
Esfuerzos tangenciales
Vamos a suponer un esfuerzo tangencial positivo \(\sigma_{yz} > 0 \) que produce una elongación normal.
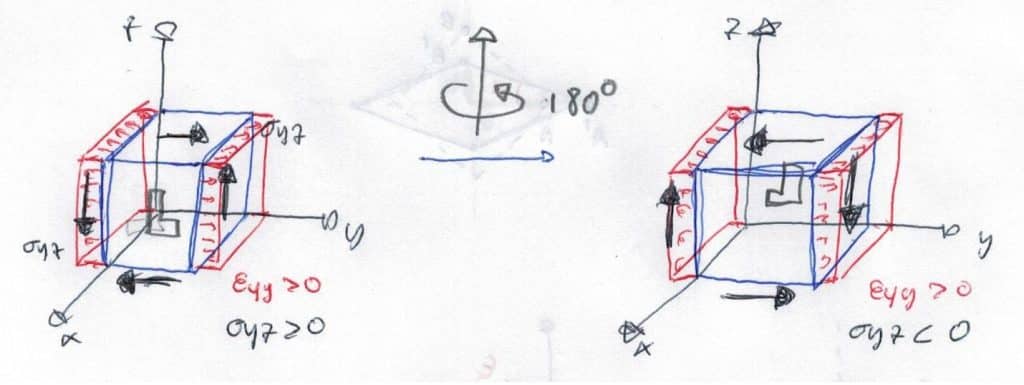
Al girar el cubo alrededor del eje z 180º, bajo el mismo sistema de referencia, el esfuerzo pasaría a ser \(\sigma_{yz} < 0 \). Sin embargo, tras cambiar el signo del esfuerzo, la deformación seguiría siendo positiva, volviendo a saltarse el concepto de lineal.
Ahora vamos a suponer el mismo esfuerzo tangencial positivo \(\sigma_{yz} > 0 \) que produce una deformación \(\epsilon_{xz} > 0 \)
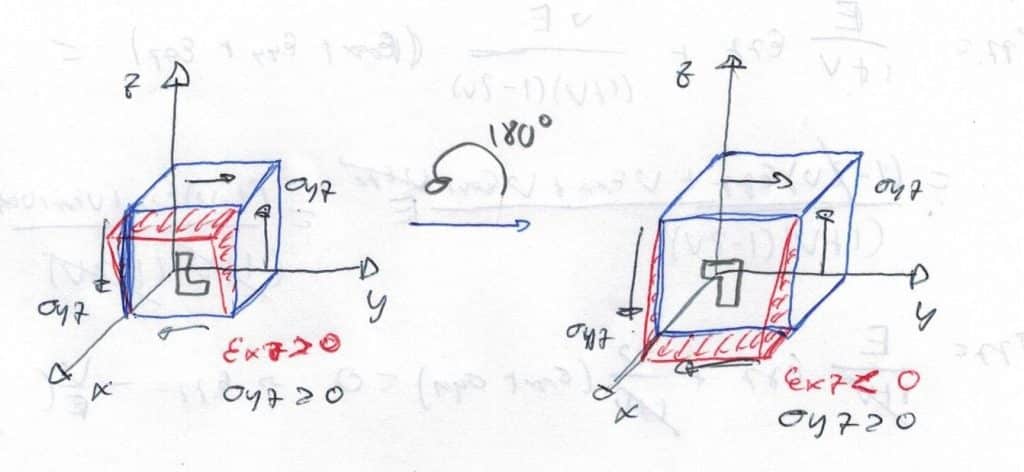
Girando el cubo 180º alrededor del eje x, el esfuerzo sigue siendo positivo. Sin embargo, la deformación ha pasado a tener el signo contrario, volviendo a incumplirse la condición de lineal
Tensor resultante
Tras el desarrollo anterior, observamos que las únicas componentes no nulas del tensor de flexibilidad son:
\( \left [ \begin{matrix} \epsilon_{xx} \\ \epsilon_{yy} \\ \epsilon_{zz} \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{matrix} \right ] = \left [ \begin{matrix} C_{11} & C_{12} & C_{13} & 0 & 0 & 0\\C_{12} & C_{22} & C_{23} & 0 & 0 & 0 \\
C_{13} & C_{23} & C_{33} & 0 & 0 & 0\\
0&0 &0 & C_{44} & 0 & 0 \\
0& 0 &0 & 0& C_{55} & 0 \\ 0&0 & 0&0 &0 & C_{66} \end{matrix} \right ] * \left [ \begin{matrix}
\sigma_{xx} \\ \sigma_{yy} \\ \sigma_{zz} \\ \sigma_{yz} \\ \sigma_{xz} \\ \sigma_{xy} \end{matrix} \right ] \)
Resultando, por ahora, sólo 9 componentes independientes
Pero, como hemos dicho, el material es isotrópico, de forma que la proporcionalidad entre esfuerzos y deformaciones debe de ser idéntica para todas las direcciones. Por ello, bajo esta hipótesis, podemos eliminar la independencia de 6 componentes, resultando únicamente 3 incógnitas para poder desarrollar la relación directa entre esfuerzo-deformación.
\( \left [ \begin{matrix} \epsilon_{xx} \\ \epsilon_{yy} \\ \epsilon_{zz} \\ – \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{matrix} \right ] = \left [ \begin{matrix} C_{11} & C_{12} & C_{12} & | & 0 & 0 & 0\\C_{12} & C_{11} & C_{12} & | & 0 & 0 & 0 \\
C_{12} & C_{12} & C_{11} & | & 0 & 0 & 0\\ – & – & – & – & – & – & – \\
0&0 &0 & | & C_{44} & 0 & 0 \\
0& 0 &0 & | & 0& C_{44} & 0 \\ 0&0 & 0& | & 0 &0 & C_{44} \end{matrix} \right ] * \left [ \begin{matrix}
\sigma_{xx} \\ \sigma_{yy} \\ \sigma_{zz} \\ – \\ \sigma_{yz} \\ \sigma_{xz} \\ \sigma_{xy} \end{matrix} \right ] \)
El por qué tomamos como independientes dichas componentes en concreto se entenderá a continuación.
Cálculo de las componentes del tensor
Diferenciamos completamente entre la parte correspondiente a las direcciones normales (1º caja) y la parte correspondiente a las direcciones tangenciales (4º caja).
Componentes normales
Vamos a comenzar estudiando el caso de un cuerpo que se somete exclusivamente a un esfuerzo normal \(\sigma_{xx}\). De el ensayo de tracción sabemos que las deformaciones que obtendremos serán:
\( \boxed{\epsilon_{xx} = \dfrac{\sigma_{xx}}{E} \ , \ \epsilon_{yy} = -\nu \dfrac{\sigma_{xx}}{E} \ , \epsilon_{yy} = -\nu \dfrac{\sigma_{xx}}{E}}\)
Aplicando el mismo concepto al resto de direcciones y empleando el principio de superposición, obtenemos que:
\(\left[\begin{matrix} \epsilon_{xx} \\ \epsilon_{yy} \\ \epsilon_{zz} \end{matrix}\right] = \left[\begin{matrix} \frac{1}{E} & -\frac{\nu}{E} & -\frac{\nu}{E} \\ -\frac{\nu}{E} & \frac{1}{E} & -\frac{\nu}{E} \\ -\frac{\nu}{E} & -\frac{\nu}{E} & \frac{1}{E} \end{matrix}\right] \left[\begin{matrix} \sigma_{xx} \\ \sigma_{yy} \\ \sigma_{zz} \end{matrix}\right] \quad \rightarrow \quad \left\{ \begin{matrix} C_{11} &=& \frac{1}{E} \\ C_{12} &=& -\frac{\nu}{E} \end{matrix} \right.\)Componentes tangenciales
La relación entre la deformación tangencial y su esfuerzo tangencial correspondiente vendrá dado por un cierto coeficiente que denominaremos como \(G\), y su relación será análoga al concepto de módulo de Young
\(\boxed{\gamma_{ij} = \dfrac{\sigma_{ij}}{G}} \ , \ con \ i \not = j\)
Definimos \(G\) como el módulo de cizalla, y a continuación obtendremos su valor por medio de constantes conocidas.
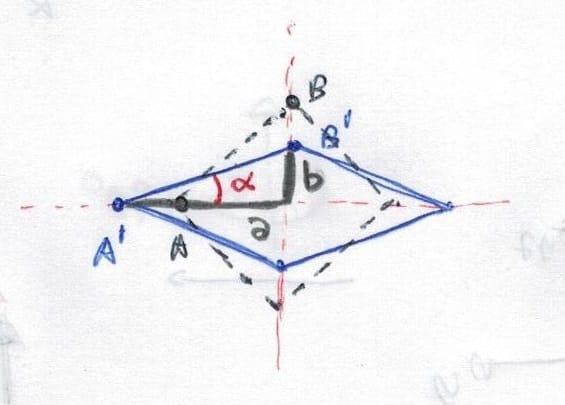
Vamos a suponer un cuadrado cuyas esquinas se someten a un esfuerzo de tracción y de compresión de igual magnitud en direcciones perpendiculares. La diagonal completa del cuadrado mide 2L.

El esfuerzo que se producirá en las caras será puramente tangencial y de valor igual al de los esfuerzos normales (Tal y como indica el círculo de Mohr para una dirección que coincide con la bisectriz de las direcciones de esfuerzos normales, donde el esfuerzo tangencial es máximo)
En primer lugar, vamos a explicitar la deformación de los puntos A y B en función de los esfuerzos aplicados:
\(\left\{ \begin{matrix} \epsilon_{A} = \frac{\sigma}{E} – \frac{\nu}{E}(-\sigma) = \sigma \frac{(1+\nu)}{E} \\ \epsilon_{B} = \frac{-\sigma}{E} – \frac{\nu}{E}\sigma = -\sigma \frac{(1+\nu)}{E} \end{matrix} \right. \quad ; \quad \left\{ \begin{matrix} a = OA + AA’ = L + L\epsilon_{A} = L\left(1+\sigma\frac{(1+\nu)}{E}\right) \\ b = OB + BB’ = L + L\epsilon_{B} = L\left(1-\sigma\frac{(1+\nu)}{E}\right) \end{matrix} \right.\)
Por otra parte, vamos a analizar la deformación desde un punto de vista geométrico;
Tras la deformación, obtendremos un ángulo \(\alpha\) cuya tangente verifica:
\(\tan{(\alpha)} = \frac{b}{a} = \frac{L \left (1-\sigma \frac{(1+\nu)}{E} \right )}{L \left (1+\sigma \frac{(1+\nu)}{E} \right )} \rightarrow \boxed{\tan{(\alpha)} =\frac{ 1-\sigma \frac{(1+\nu)}{E} }{ 1+\sigma \frac{(1+\nu)}{E} }}\)El ángulo \(\alpha\) vendrá dado por:
\(2 \alpha = \frac{\pi}{2} – \gamma \rightarrow \boxed{\alpha = \frac{\pi}{4} – \frac{\gamma}{2}}, \ \ \ \ Recordemos \ que \ \epsilon =\frac{\gamma}{2} \)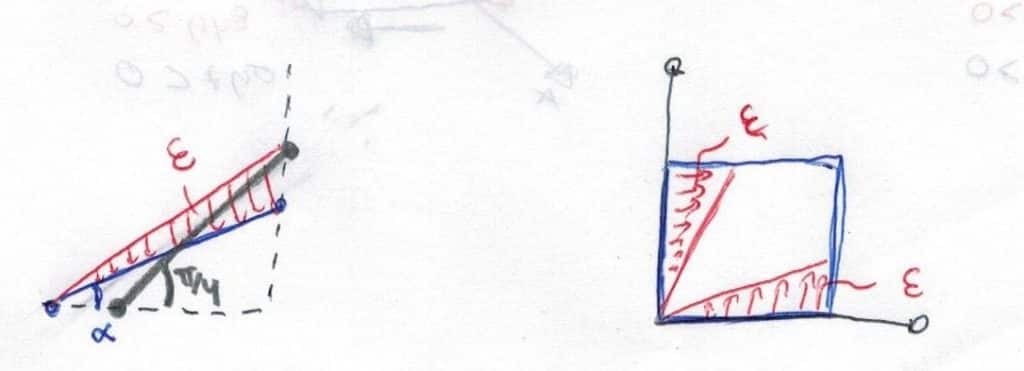
Recordando que:
\( \tan{(a-b)} = \frac{\tan{(a)} – \tan{(b)} }{1+\tan{(a)}*\tan{(b)}} \rightarrow \rightarrow \\ \) \( \rightarrow \tan{(\alpha)} = \tan{( \frac{\pi}{4} – \frac{\gamma}{2} )} = \frac{\tan{(\frac{\pi}{4})} – \tan{(\frac{\gamma}{2})} }{1+\tan{(\frac{\pi}{4})}*\tan{(\frac{\gamma}{2})}} = \frac{1 – \tan{(\frac{\gamma}{2})} }{1+\tan{(\frac{\gamma}{2})}} \rightarrow \\ \) \( \rightarrow \frac{1 – \tan{(\frac{\gamma}{2})} }{1+\tan{(\frac{\gamma}{2})}} \approx \frac{ 1 – \frac{\gamma}{2} }{1+\frac{\gamma}{2}} \rightarrow \left \{ \gamma_{ij} = \frac{\sigma_{ij}}{G} \right \} \rightarrow \boxed{ \frac{ 1 – \frac{\sigma}{2*G} }{1+\frac{\sigma}{2*G}} = \tan{(\alpha)}} \)\(\left\{ \begin{matrix} 1) & \tan(\alpha) &=& \dfrac{1 – \dfrac{\sigma}{2G}}{1 + \dfrac{\sigma}{2G}} \\ \\ 2) & \tan(\alpha) &=& \dfrac{1 – \sigma\dfrac{(1+\nu)}{E}}{1 + \sigma\dfrac{(1+\nu)}{E}} \end{matrix} \right.\)
\(\iff \boxed{ G = \frac{E}{2(1+\nu)}} \ ; \ \ \ \ \rightarrow \ \ \ C_{44} = \frac{1}{G}\)
Forma final del tensor
Tras hallar el valor de las componentes de nuestro tensor de flexibilidad, la relación final entre las componentes del tensor de deformaciones y esfuerzos es:
\( \left [ \begin{matrix} \epsilon_{xx} \\ \epsilon_{yy} \\ \epsilon_{zz} \\ – \\ \gamma_{yz} \\ \gamma_{xz} \\ \gamma_{xy} \end{matrix} \right ] = \left [ \begin{matrix} \frac{1}{E} & -\frac{\nu}{E} & -\frac{\nu}{E} & | & 0 & 0 & 0\\
-\frac{\nu}{E} & \frac{1}{E} &-\frac{\nu}{E}& | & 0 & 0 & 0 \\
-\frac{\nu}{E} & -\frac{\nu}{E} & \frac{1}{E} & | & 0 & 0 & 0\\ – & – & – & – & – & – & – \\
0&0 &0 & | & 2\frac{(1+\nu)}{E} & 0 & 0 \\
0& 0 &0 & | & 0&2\frac{(1+\nu)}{E} & 0 \\ 0&0 & 0& | & 0 &0 & 2\frac{(1+\nu)}{E}\end{matrix} \right ] * \left [ \begin{matrix}
\sigma_{xx} \\ \sigma_{yy} \\ \sigma_{zz} \\ – \\ \sigma_{yz} \\ \sigma_{xz} \\ \sigma_{xy} \end{matrix} \right ] \)
Que, en notación tensorial, queda:
\( \boxed{\epsilon_{ij} = \frac{1}{E} \left [(1+\nu)* \sigma_{ij} – \nu * \sigma_{kk} * \delta_{ij} \right ]}\)
Esfuerzos en función de deformaciones
Una vez definida por completo la dependencia de \(\epsilon \ y \ \sigma\), estamos interesados en obtener la forma inversa, es decir, las tensiones en función de las deformaciones. Lo haremos manipulando algebráicamente la forma en notación tensorial.
En primer lugar, despejamos el \(\sigma_{ij}\):
\( \epsilon_{ij} = \frac{1}{E} \left [(1+\nu)* \sigma_{ij} – \nu * \sigma_{kk} * \delta_{ij} \right ] \ \rightarrow \ \sigma_{ij}= \frac{E}{1+\nu}\epsilon_{ij} + \frac{\nu}{1+\nu}* \sigma_{kk} * \delta_{ij} \)Ahora necesitamos saber el valor de \(\sigma_{kk} \) en función de las deformaciones. Para obtener su valor, sumamos \(\epsilon_{ij}\) para i=j=1,2,3 , que coincide con la notación de \(\epsilon_{kk}\):
\(\epsilon_{kk} = \frac{1}{E}[(1+\nu)*\sigma_{kk} + 3 *( -\nu * \sigma_{kk})] \ \rightarrow \ \epsilon_{kk} = \frac{(1-2\nu)}{E}\sigma_{kk} \ \rightarrow \) \( \rightarrow \boxed{\sigma_{kk} =\frac{E}{1-2\nu}\epsilon_{kk} }\)Introduciendo en la fórmula:
\(\boxed{\sigma_{ij}= \frac{E}{1+\nu}\epsilon_{ij} + \frac{\nu*E}{(1+\nu)(1-2\nu)}\epsilon_{kk} * \delta_{ij}} \)
Definiendo la constante de Lamé como \(\lambda = \frac{\nu*E}{(1+\nu)(1-2\nu)}\) y expresando el módulo de Young y el coeficiente de Poisson en función del módulo de cizalla obtenemos una forma más reducida:
\( \boxed{\sigma_{ij}= 2G\epsilon_{ij} + \lambda \epsilon_{kk}* \delta_{ij}} \)
Valor admisible de las constantes
Hemos usado un total de 4 constantes a lo largo del desarrollo del tensor de flexibilidad y rigidez. Pero realmente, independientes son \(E \ y \ \nu\).
Por pura coherencia termodinámica, el valor de E debe de ser siempre mayor a 0, es decir, \(\boxed{E>0}\). Esto ocurre porque, cuando aplicamos un esfuerzo positivo, debemos de obtener una deformación positiva, de forma que la densidad de trabajo realizado sobre el cuerpo deformado sea positiva. De lo contrario, los cuerpos se deformarían por sí mismos y además cederían trabajo al entorno.
Para estimar el valor del coeficiente de Poisson vamos a suponer un estado hidrostático. En este caso, los esfuerzos son \(\sigma_{ij}=-P \delta_{ij}\).
La deformación volumétrica, como introducimos en el artículo anterior, es igual a la suma de la diagonal, o lo que es lo mismo:
\(\bigtriangleup V = \epsilon_{kk} = \frac{1-2\nu}{E} \sigma_{kk} = \frac{-3 P }{E} (1-2 \nu) \); lo que implica una reducción del volumen sólo si \(\nu < 0.5\). Como es lógico, un cuerpo que se somete exclusivamente a esfuerzos de compresión, únicamente puede reducir su volumen (Y además, debe de reducirse aunque sea muy poco, porque un esfuerzo obliga a la generación de una deformación. Por ello es <).
Además, en general, cuando un material aumenta su longitud, su sección transversal se queda igual o disminuye, de forma que \(\epsilon_{longitudinal}*\epsilon_{transversal} \leq 0 \iff \nu \geq 0 \).
(Digo en general porque existen los materiales augéticos los cuales presentan un coeficiente de Poisson negativo. Pero esto ocurre a nivel molecular y en un grupo reducidísimo de materiales)
Por lo tanto, los valores normales del coeficiente de Poisson son \(\boxed{0 \leq \nu < 0.5}\)
Como el módulo de cizalla y la constante de Lamé dependen exclusivamente del coeficiente de Poisson y el módulo de Young, la obtención de sus valores admisibles es instantánea:
\(\left\{ \begin{matrix} \boxed{G > 0} \\ \\ \boxed{\lambda \geq 0} \end{matrix} \right.\)Artículo siguiente:

![[Elasticidad y Resistencia de Materiales] Teoría de la Elasticidad Portada-elasticidad-alta](https://ingenieriabasica.es/wp-content/uploads/2020/07/Portada-elasticidad-alta-200x136.jpg)