Artículo anterior:
En el artículo anterior hemos desarrollado el concepto de tensión y hemos definido el estado tensional y el tensor de tensiones. Además, hemos visto qué ecuaciones deben de cumplir las componentes del tensor para ser considerado válido. En este artículo desarrollaremos las características y formas alternativas del tensor de tensiones.
Imágenes tomadas del libro “Teoría de la Elasticidad” de Federico París, profesor de la ETSI.
Formas características del Tensor de Tensiones
Podemos expresar nuestro tensor de tensiones de diferentes maneras cambiando el sistema de referencia o separando el tensor en dos partes en función de sus propiedades
Direcciones Principales
Recordemos cómo se relaciona el vector tensión con la normal de una superficie:
\( \sigma_{ij}*n_{j}=T_{i} \)
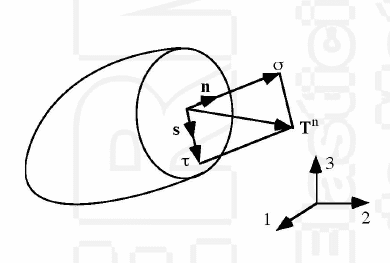
Ya dijimos anteriormente que no tiene por qué coincidir con la normal. Pero… ¿Puede ser que si cortamos nuestro cuerpo con una orientación determinada, hagamos coincidir el vector tensión con nuestra normal?
La respuesta es sí.
En ese caso, recordando la representación en componentes intrínsecas tendríamos que
\(\vec{T} \parallel \vec{n} \rightarrow \vec{T}= [\sigma]*\vec{n} = \underbrace{\sigma_{n}}_{escalar}* \ \vec{n} \ \ \ \iff \ \ \ ([\sigma]-\sigma_{n}[I])*\vec{n}=0\)
Lo que nos genera el siguiente sistema de ecuaciones:
\(\left \{ \begin{matrix} (\sigma_{11} – \sigma_{n}) \cdot n_{1} + \sigma_{12} \cdot n_{2} + \sigma_{13} \cdot n_{3} = 0 \\ \\ \sigma_{12} \cdot n_{1} + (\sigma_{22} – \sigma_{n}) \cdot n_{2} + \sigma_{23} \cdot n_{3} = 0 \\ \\ \sigma_{13} \cdot n_{1} + \sigma_{23} \cdot n_{2} + (\sigma_{33} – \sigma_{n}) \cdot n_{3} = 0 \end{matrix} \right. \rightarrow \left [ \begin{matrix} \sigma_{11} – \sigma_{n} & \sigma_{12} & \sigma_{13} \\ \sigma_{12} & \sigma_{22} – \sigma_{n} & \sigma_{23} \\ \sigma_{13} & \sigma_{23} & \sigma_{33} – \sigma_{n} \end{matrix} \right ] \left [ \begin{matrix} n_{1} \\ n_{2} \\ n_{3} \end{matrix} \right ] = \left [ \begin{matrix} 0 \\ 0 \\ 0 \end{matrix} \right ] \)Siguiendo los concimientos básicos de resolución de ecuaciones llegamos a la conclusión que en caso de SCD, la solución única es la solución trivial
\(\left [ \begin{matrix} n_{1} \\ n_{2} \\ n_{3} \end{matrix} \right ] = \left [ \begin{matrix} 0 \\ 0 \\ 0 \end{matrix} \right ] \)
Sin embargo esa solución, no es válida. No sólo porque no aporta nada, sino porque haría incompatible la definición de vector normal unitario tal que \(n_{1}^{2}+ n_{2}^{2}+ n_{3}^{2} = 1\)
Observamos que la única solución es escoger meticulosamente los valores de \(\sigma_{n}\) de tal forma que hagamos el sistema SCI y obtengamos infinitas soluciones dependientes de un parámetro. Entramos en el clásico problema de autovalores y autovectores, donde nuestros autovalores (Valores de \(\sigma_{n}\) ) se obtienen verificando la condición
\(det ([\sigma]-\sigma_{n}[I]) = \left | \begin{matrix} \sigma_{11} – \sigma_{n} & \sigma_{12} & \sigma_{13} \\ \sigma_{12} & \sigma_{22} – \sigma_{n} & \sigma_{23} \\ \sigma_{13} & \sigma_{23} & \sigma_{33} – \sigma_{n} \end{matrix} \right |= 0\)
Invariantes
Desarrollando el determinante llegaríamos a una ecuación polinómica de tercer grado de la forma:
\(\sigma_{n}^{3} – I_{1}\sigma_{n}^{2} + I_{2} \sigma_{n} – I_{3}=0\)
Pero, ¿Por qué cambio el signo alternativamente y qué significan los coeficientes I?
Los términos \(I_{1}, I_{2}, I_{3}\) se denominan invariantes, y su utilidad radica en que una vez dada su definición, su cálculo es independiente del sistema de referencia. Es decir, podremos obtener los coeficientes de nuestra ecuación sin tener que desarrollar el determinante y siendo válido aunque nuestro tensor se encuentre girado.
\(\left \{ \begin{matrix} I_{1} = \text{tr}([\sigma]) = \sigma_{11} + \sigma_{22} + \sigma_{33} \\ \\ I_{2} = \left | \begin{matrix} \sigma_{11} & \sigma_{12} \\ \sigma_{12} & \sigma_{22} \end{matrix} \right | + \left | \begin{matrix} \sigma_{11} & \sigma_{13} \\ \sigma_{13} & \sigma_{33} \end{matrix} \right | + \left | \begin{matrix} \sigma_{22} & \sigma_{23} \\ \sigma_{23} & \sigma_{33} \end{matrix} \right | = \sigma_{11} \sigma_{22} + \sigma_{11} \sigma_{33} + \sigma_{22} \sigma_{33} – \sigma_{12}^{2} – \sigma_{23}^{2} – \sigma_{23}^{2} \\ \\ I_{3} = \text{Det}([\sigma]) = \left | \begin{matrix} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{12} & \sigma_{22} & \sigma_{23} \\ \sigma_{13} & \sigma_{23} & \sigma_{33} \end{matrix} \right | \end{matrix} \right. \)Unos buenos consejos para jamás olvidar los signos y la definición de cada invariante es:
- La secuencia es + – + – , comenzando el primer término con signo positivo (Como es típico en la escritura de las ecuaciones polinómicas)
- Los invariantes tienen unidades físicas de forma que al multiplicarse por la incógnita son siempre \( [MPa]^{3}\). De esta forma, la traza \(( [MPa] ) \) multiplica al término al cuadrado \(( [MPa] ^{2}) \) mientras que el determinante \(( [MPa] ^{3} ) \) va solo
- La suma de la diagonal (Traza) es igual a la suma de los autovalores, siendo una propiedad básica de las matrices.
Una vez escrita nuestra ecuación y resuelta, obtendremos 3 soluciones, las cuales denominaremos \(\sigma_{I}, \sigma_{II} , \sigma_{III} \), los cuales pueden tomar cualquier valor (Negativo, 0, pueden tener todos el mismo valor) pero los ordenaremos siempre como \(\sigma_{I} \geq \sigma_{II} \geq \sigma_{III} \)
Una vez obtenido cada uno de los autovalores deberemos de obtener los autovectores. Para cada uno de nuestros \(\sigma_{I}, \sigma_{II} , \sigma_{III} \), resolviendo el sistema obtendremos una normal \(\vec{n}_{I}, \vec{n} _{II} , \vec{n} _{III} \) de tal forma que en esa dirección nuestro vector tensión coincide con la normal. Expresadas en base a nuestro sistema {1,2,3}, obtendremos unos valores de la forma (Por ejemplo)
\(\vec{n}_{I}= \left [ \begin{matrix} \frac{\sqrt{2}}{2} \\ 0 \\ \frac{\sqrt{2}}{2} \end{matrix} \right ]_{\{1,2,3\}} \ \ \ \ \ \ \vec{n} _{II}= \left [ \begin{matrix} -\frac{\sqrt{2}}{2} \\ 0 \\ \frac{\sqrt{2}}{2} \end{matrix} \right ]_{\{ 1,2,3 \}} \ \ \ \ \ \ \vec{n} _{III}= \left [ \begin{matrix} 0 \\ 1 \\ 0 \end{matrix} \right ]_{\{ 1,2,3 \}} \)Los autovalores que obtengamos serán todos REALES (No números complejos). Esto se debe a que el tensor es una matriz simétrica.
Alternativamente podemos tomar un nuevo sistema de referencia alternativo al {1,2,3} que llamaremos sistema de ejes principales {I,II,III} el cual se define por las direcciones:
\( \vec{n} _{I}= \left [ \begin{matrix} 1 \\ 0 \\ 0 \end{matrix} \right ]_{\{I,II,III\}} \ \ \ \ \ \ \vec{n} _{II}= \left [ \begin{matrix} 0 \\ 1 \\ 0 \end{matrix} \right ]_{\{I,II,III\}} \ \ \ \ \ \ \vec{n} _{III}= \left [ \begin{matrix} 0 \\ 0 \\ 1 \end{matrix} \right ]_{\{I,II,III\}} \)De forma que, expresando nuestro tensor de tensiones referido a dicho sistema principal (Estaríamos girando el tensor), obtenemos un tensor diagonal:
\( \left [ \begin{matrix} \sigma_{I} & 0 & 0 \\ 0 & \sigma_{II} & 0 \\ 0 & 0 & \sigma_{III} \end{matrix} \right ] \)
Que es el mismo tensor/estado tensorial pero bajo otro sistema de referencia. Lo que hemos hecho ha sido girar el sistema de referencia y colocarlo apropiadamente para obtener una forma diagonal. Los ejes coinciden con las direcciones principales, y como era de esperar, en dichas direcciones sólo hay esfuerzos normales.
El estado tensional es el mismo. Lo que cambiamos son los ejes en base a los cuales definimos las normales.
Características de las soluciones
Cada autovalor estará asociado como mínimo a un autovector, de manera que los 3 autovectores que obtengamos serán perpendiculares entre sí, obteniendo una terna ortonormal.
Sin embargo, dependiendo de la multiplicidad de nuestros autovalores puede que nuestra terna no sea única y tengamos la posibilidad de elegir las direcciones (Porque, dentro del abanico de posibilidades, el vector tensión sea paralelo a varias direcciones). Vamos a estudiar todos estos casos particulares.
- \(\sigma_{I} > \sigma_{II} > \sigma_{III} \rightarrow n_{I}, n_{II}, n_{III}\) son únicos.
- \(\sigma_{I} \not = \sigma_{II} = \sigma_{III} \rightarrow n_{I}\) es único mientras que podemos elegir los valores de \(n_{II},n_{III}\) en torno a un plano perpendicular a la dirección \(n_{I}\) y verificando la perpendicularidad. Se dice que es un estado cilindrico de esfuerzos donde no hay esfuerzos tangenciales “sobre las paredes del cilindro”
- \(\sigma_{I} = \sigma_{II} = \sigma_{III} \rightarrow \) Podemos elegir cualquier terna de vectores ortonormales en cualquier orientación. Se dice que es un estado esférico, donde no hay esfuerzos tangenciales.
- \(\sigma_{I} \not = \sigma_{II} , \sigma_{III} = 0 \rightarrow \) Sólo hay tensiones en las direcciones I y II. Se dice que es un estado plano.
Una vez identificado el estado tensional, podemos asegurar lo siguiente:
- Si \(\sigma_{III} \geq 0 \rightarrow \) Sólo hay esfuerzos positivos (Tracciones)
- Si \(\sigma_{I} \leq 0 \rightarrow \) Sólo hay esfuerzos negativos (Compresiones)
- Si no se cumple ninguno de los casos, hay una mezcla de tracción y compresión
Tensor esférico y desviador
Esta forma especial divide el tensor en una suma de una parte esférica (Tensor diagonal que contiene las “tensiones de presión”) y una parte desviadora obtenida por la diferencia entre tensores.
Es una de las múltiples formas de expresar el tensor de tensiones, y su utilidad radica en las propiedades de cada tensor, estando por ejemplo el esférico asociado a la variación de volumen y el desviador a la variación de forma, entre otros.
\(\sigma_{esf}= \frac{tr([\sigma])}{3}= \frac{ \sigma_{11}+ \sigma_{22} + \sigma_{33} }{3} = \frac{\sigma_{I}+ \sigma_{II} + \sigma_{III} }{3} \)
\( [\sigma] = [\sigma_{esferico}]+[\sigma_{desviador}]\)
\( \left [ \begin{matrix} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{12} & \sigma_{22} & \sigma_{23} \\ \sigma_{13} & \sigma_{23} & \sigma_{33} \end{matrix} \right ] = \left [ \begin{matrix} \sigma_{esf} & 0 & 0 \\ 0 & \sigma_{esf} & 0 \\ 0 & 0 & \sigma_{esf} \end{matrix} \right ] + \left [ \begin{matrix} \sigma_{11} – \sigma_{esf} & \sigma_{12} & \sigma_{13} \\ \sigma_{12} & \sigma_{22} – \sigma_{esf} & \sigma_{23} \\ \sigma_{13} & \sigma_{23} & \sigma_{33} – \sigma_{esf} \end{matrix} \right ] \)
Valores máximos y mínimos de tensión tangencial
Partiendo de un sistema de referencia de ejes principales, queremos conocer las direcciones en las que los esfuerzos normales (En valor absoluto) son máximos/mínimos, así como en las que los esfuerzos tangenciales sean máximos/mínimos.
Tensiones normales
Empleando la relación de Cauchy:
\(\vec{T}=\left [ \begin{matrix} \sigma_{I} & 0 & 0 \\ 0 & \sigma_{II} & 0 \\ 0 & 0 & \sigma_{III} \end{matrix} \right ] * \left [ \begin{matrix} n_{1} \\ n_{2} \\ n_{3} \end{matrix} \right ]_{\{I,II,III\}} = \left ( \begin{matrix} \sigma_{I} * n_{1} \\ \sigma_{II} * n_{2} \\ \sigma_{III} * n_{3} \end{matrix} \right )\)
La componente normal viene dada por
\(\sigma_{n}= \vec{T} * \vec{n} =\sigma_{I}n_{1}^{2} + \sigma_{II}n_{2}^{2} + \sigma_{III}n_{3}^{2} \)Teniendo en cuenta que \(n_{1}^{2}+ n_{2}^{2}+ n_{3}^{2}=1\), expresando \(n_{3}^{2}=1-n_{1}^{2} – n_{2}^{2} \rightarrow\)
\( \rightarrow \sigma_{n}=\sigma_{n}(n_{1},n_{2})=n_{1}^{2}(\sigma_{I}- \sigma_{III} ) + n_{2}^{2}( \sigma_{II} – \sigma_{III} ) + \sigma_{III} \)Los valores extremos se obtienen con:
\(\left \{ \begin{matrix} \frac{\partial \sigma_{n}}{\partial n_{1}} = 0 \rightarrow 2(\sigma_{I} – \sigma_{III})n_{1} = 0 \\ \\ \frac{\partial \sigma_{n}}{\partial n_{2}} = 0 \rightarrow 2(\sigma_{II} – \sigma_{III})n_{2} = 0 \end{matrix} \right. \rightarrow\)\(\rightarrow\) Máximo en \( n_{1}=n_{2}=0 \iff n_{3}=\pm 1\)
Aplicando lo mismo para el resto de cambios \(n_{2}^{2}=1-n_{1}^{2} – n_{3}^{2} \ \ \ , \ \ \ n_{1}^{2}=1-n_{2}^{2} – n_{3}^{2} \) ,obtenemos las direcciones de máximos esfuerzos normales en:
\(n = \pm n_{I} = \left ( \begin{matrix} \pm 1 \\ 0 \\ 0 \end{matrix} \right )\)
\( n= \pm n_{II} = \left ( \begin{matrix} 0 \\ \pm 1 \\ 0 \end{matrix} \right ) \)
\( n= \pm n_{III} =\left ( \begin{matrix} 0 \\ 0 \\ \pm 1 \end{matrix} \right ) \)
Que coinciden con nuestros ejes principales. Era un resultado obvio ya que en estas direcciones, como hemos demostrado anteriormente, la tensión es únicamente normal, y por lo tanto es un punto extremo al ser la tensión tangencial 0 en estas direcciones y aumentar a medida que nos separamos.
Tensiones tangenciales
La componente tangencial puede ser expresada de la forma \(\tau = \sqrt{(\vec{T})^{2} – \sigma_{n}^{2}}\)
Introduciendo los valores de \(\vec{T} \ y \ \sigma_{n}\) así como realizando el cambio \(n_{3}^{2}=1-n_{1}^{2} – n_{2}^{2} \)
\(\tau = \tau(n_{1},n_{2})=\sqrt{\sigma_{I}^{2}n_{1}^{2}+ \sigma_{II}^{2}n_{2}^{2}+ \sigma_{III}^{2}( 1-n_{1}^{2} – n_{2}^{2} )^{2} – ( \sigma_{I}n_{1}^{2} + \sigma_{II}n_{2}^{2} + \sigma_{III} ( 1-n_{1}^{2} – n_{2}^{2} ) )^{2}} \)Calculando los valores extremos al igual que con las tensiones normales:
\(\left \{ \begin{matrix} \frac{\partial \tau}{\partial n_{1}} = 0 \\ \\ \frac{\partial \tau}{\partial n_{2}} = 0 \end{matrix} \right. \)Obtenemos los siguientes valores extremos:
Máximos
\( n= \left ( \begin{matrix} 0 \\ \pm \sqrt{\frac{1}{2}} \\ \pm \sqrt{\frac{1}{2}} \end{matrix} \right ) \)
\(n= \left ( \begin{matrix} \pm \sqrt{\frac{1}{2}} \\ 0 \\ \pm \sqrt{\frac{1}{2}} \end{matrix} \right ) \)
\(n= \left ( \begin{matrix} \pm \sqrt{\frac{1}{2}} \\ \pm \sqrt{\frac{1}{2}} \\0 \end{matrix} \right ) \)
Mínimos
\(n = \pm n_{I} = \left ( \begin{matrix} \pm 1 \\ 0 \\ 0 \end{matrix} \right )\)
\( n= \pm n_{II} = \left ( \begin{matrix} 0 \\ \pm 1 \\ 0 \end{matrix} \right ) \)
\( n= \pm n_{III} =\left ( \begin{matrix} 0 \\ 0 \\ \pm 1 \end{matrix} \right ) \)
Recordemos que nos referimos a n como \(n=\left ( \begin{matrix} n_{1} \\ n_{2} \\ n_{3} \end{matrix} \right )_{\{I,II,III\}}\)
Observamos que obtenemos unos resultados coherentes. Los valores mínimos se alcanzan en las direcciones donde no existen tensiones tangenciales, y los valores máximos se alcanzan en las bisectrices de las direcciones principales, es decir, las direcciones que se encuentran más alejadas de las correspondientes a los esfuerzos puramente normales.
Introduciendo los valores de las normales en nuestra ecuación de \(\tau\) obtenemos como valores máximos:
\(\left\{ \begin{array}{l} \tau_{I} = \frac{\sigma_{II} – \sigma_{III}}{2} \\ \\ \tau_{II} = \frac{\sigma_{I} – \sigma_{III}}{2} \\ \\ \tau_{III} = \frac{\sigma_{I} – \sigma_{II}}{2} \end{array} \right. \)
Asumiendo que \(\sigma_{I}>\sigma_{II}>\sigma_{III}\), observamos que el máximo esfuerzo tangencial es el \(\tau_{II}\), el cual se encuentra en la bisectriz de I y III
El Elipsoide de Lamé
Una forma gráfica de visualizar los esfuerzos normales es mediante la definición de un elipsoide basado en los autovalores.
Partiendo de la definición de las componentes del vector tensión (En direcciones principales):
\(\vec{T} = [\sigma] \cdot \vec{n} = \left\{ \begin{array}{l} T_{1} = \sigma_{I} \cdot n_{1} \\ T_{2} = \sigma_{II} \cdot n_{2} \\ T_{3} = \sigma_{III} \cdot n_{3} \end{array} \right. \rightarrow \left\{ \begin{array}{l} n_{1} = \frac{T_{1}}{\sigma_{I}} \\ n_{2} = \frac{T_{2}}{\sigma_{II}} \\ n_{3} = \frac{T_{3}}{\sigma_{III}} \end{array} \right.\)
Introduciendo los valores de n en la ecuación \(n_{1}^{2}+n_{2}^{2}+n_{3}^{2}=1 \ \rightarrow\)
\(\ \rightarrow \boxed{\frac{T_{1}^{2}}{\sigma_{I}^{2}} + \frac{T_{2}^{2}}{\sigma_{II}^{2}} + \frac{T_{3}^{2}}{\sigma_{III}^{2}}=1}\)
Que representa la distribución espacial de los esfuerzos normales, tomando como ejes de referencia los ejes principales y variando los valores de las componentes de T como si de las coordenadas x,y,z de un elipsoide se tratase.
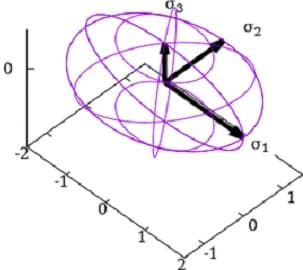
Si las tres tensiones principales son estrictamente positivas, se describe un elipsoide real. Si alguno de los autovalores fuesen negativos, el elipsoide sería imaginario. Tampoco estaría bien definido en caso de autovalor nulo. Si todas las tensiones principales son positivas, la tensión normal siempre ha de ser positiva, es decir, de tracción, sin importar la dirección del vector normal a la superficie en la que se mide la tensión.
Casos partículares
Estado esférico (Esfera)
Todos los autovalores \(\sigma_{I,II,III}\) tienen el mismo valor. En ese caso los esfuerzos son puramente normales en todas las direcciones y de igual valor. Obtenemos una esfera. Decimos que estamos en un caso de tensión esférica. Es el estado de esfuerzos que se da por presión en un fluido.
Estado cilíndrico de esfuerzos (Elipsoide de revolución)
Ocurre cuando 2 de los autovalores son idénticos. En ese caso, se obtiene un elipsoide de revolución alrededor del eje perteneciente al autovalor diferente. Tenemos esfuerzos puramente normales y de igual magnitud en las direcciones de igual valor.
Estado plano (Circunferencia)
Ocurre cuando uno de los autovalores es nulo. En ese caso, la ecuación se transforma en la ecuación de una circunferencia.
El Círculo de Mohr
El círculo de Mohr es una poderosa herramienta que nos ayuda a localizar geométricamente los valores de \(\sigma \ y \ \tau\) para una dirección dada (\(\vec{n}\)) y viceversa. Vamos a empezar colocando un sistema de ecuaciones ya conocidas:
\(\left\{ \begin{matrix} \|\vec{T}\|^2 & = & \sigma_{I}^{2} n_{1}^{2} + \sigma_{II}^{2} n_{2}^{2} + \sigma_{III}^{2} n_{3}^{2} & = & \sigma^{2} + \tau^{2} \\ \vec{T} \cdot \vec{n} & = & \sigma_{I} n_{1} + \sigma_{II} n_{2} + \sigma_{III} n_{3} & = & \sigma \\ \|\vec{n}\|^2 & = & n_{1}^{2} + n_{2}^{2} + n_{3}^{2} & = & 1 \end{matrix} \right.\)
Observamos que es un sistema de ecuaciones para los valores de \(n_{1}^{2}, n_{2}^{2} , n_{3}^{2}\) con solución única, es decir, no dependen las soluciones de ningún parámetro.
Pero… ¿Cómo obtenemos la solución para cada valor de n despejado? Tendríamos que recurrir a métodos matriciales o elaborar cuentas muy largas… O seguir el siguiente truco.
Vamos a definir la función \(f(\sigma) = \sigma^{2} + b\sigma + c \). Ahora, multiplicamos la segunda fila por b y la tercera fila por c. Y las sumamos, obteniendo:
\(\boxed{n_{1}^{2}*f(\sigma_{I}) + n_{2}^{2}*f(\sigma_{II}) + n_{3}^{2}*f(\sigma_{III}) = f(\sigma) + \tau^{2}}\)
Ahora viene el truco. Suponemos que elegimos los valores de b y c tal que elaboramos una forma de la función\(f(\sigma)\) que nos convenga para eliminar los coeficientes que no nos interesan de n.
\((1) \ Para \ f(\sigma)=(\sigma-\sigma_{II})(\sigma-\sigma_{III}) \rightarrow n_{1}^{2}=\frac{(\sigma-\sigma_{II})(\sigma-\sigma_{III}) + \tau^{2}}{(\sigma_{I}-\sigma_{II})(\sigma_{I}-\sigma_{III})} \geq 0\) \((2) \ Para \ f(\sigma)=(\sigma-\sigma_{I})(\sigma-\sigma_{III}) \rightarrow n_{2}^{2}=\frac{(\sigma-\sigma_{I})(\sigma-\sigma_{III}) + \tau^{2}}{(\sigma_{II}-\sigma_{I})(\sigma_{II}-\sigma_{III})} \geq 0\) \((3) \ Para \ f(\sigma)=(\sigma-\sigma_{I})(\sigma-\sigma_{II}) \rightarrow n_{3}^{2}=\frac{(\sigma-\sigma_{I})(\sigma-\sigma_{II}) + \tau^{2}}{(\sigma_{III}-\sigma_{I})(\sigma_{III}-\sigma_{II})} \geq 0\)En el primer caso por ejemplo, al establecer esa forma de \(f(\sigma)\), obtenemos que \(f(\sigma_{II})=f(\sigma_{III})=0\), pudiendo despejar fácilmente \(n_{1}^{2}=\frac{f(\sigma) + \tau^{2}}{f(\sigma_{I})}\)
Observamos que es condición que todas las fracciones den un resultado positivo para que la combinación de \(\sigma \ y \ \tau\) sea coherente. Volviendo a asumir que \(\sigma_{I} > \sigma_{II} > \sigma_{III}\), certificamos que los denominadores de (1) y (3) son positivos, mientras que el denominador de (2) es negativo. Siguiendo este criterio, las restricciones finales que nos darán el dominio válido de nuestro círculo de Mohr resulta ser la intersección de las regiones:
\(\boxed{(\sigma-\sigma_{II})(\sigma-\sigma_{III}) + \tau^{2} \geq 0}\)
\(\boxed{(\sigma-\sigma_{I})(\sigma-\sigma_{III}) + \tau^{2} \leq 0}\)
\(\boxed{(\sigma-\sigma_{I})(\sigma-\sigma_{II}) + \tau^{2} \geq 0}\)
Recordamos que la ecuación de una circunferencia centrada en el eje y, y desplazada a lo largo del eje x tiene la forma:
\(\left( (x-a)^{2} + y^{2} – R^{2} \right) = 0 \rightarrow \left( (x-a+R)(x-a-R) + y^{2} \right) = \\ 0 \rightarrow \left( (x-A)(x-B) + y^{2} \right) = 0\)
En función de los valores de \(\sigma_{I,II,III}\), obtendremos algo así:
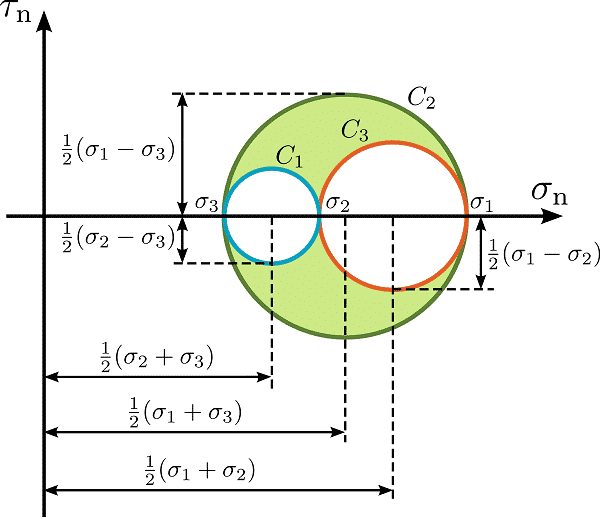
Donde, como observamos, los valores máximos de \(\tau\) se alcanzan en los puntos intermedios a los esfuerzos normales, y podemos calcular su valor fácilmente de forma geométrica. La zona válida es la zona verde, delimitada por las 3 circunferencias. Además, observamos que el valor de los esfuerzos tangenciales es nulo para los valores de \(\sigma_{I,II,III}\).
Observamos que los valores de \(\sigma\) también pueden ser negativos, de manera que el círculo se encontraría a ambos lados del eje y. Esta es la condición necesaria (Tener autovalores de distinto signo) para asegurar la existencia de una dirección en la cual no hay esfuerzos normales. Ocurriría para el \(\tau\) asociado a \(\sigma=0\)
En un problema plano o cuando dos autovalores tengan el mismo valor, el dominio admisible (Región delimitada por las 3 circunferencias) pasaría a ser el de una circunferencia generada por los 2 autovalores diferentes.
Artículo siguiente:

![[Elasticidad y Resistencia de Materiales] Teoría de la Elasticidad Portada-elasticidad-alta](https://ingenieriabasica.es/wp-content/uploads/2020/07/Portada-elasticidad-alta-200x136.jpg)