¿Cuál es el mecanismo de un botijo?

“Eres más simple que el mecanismo de un botijo”. Es uno de los refranes más populares pero… ¿Cuál es el mecanismo de un botijo? ¿Por qué es tan simple?

Haciendo un sondeo entre amigos y familiares me suelen dar una respuesta que se parece a esta: “Bueno, porque un botijo es un objeto cuya función es almacenar agua y tiene agujeritos para llenarlo y vaciarlo. No tiene más, así de simple”.

Y en parte están en lo cierto. Lo que ocurre es que la gran mayoría no sabe que el botijo como tal cumple una función muy útil más allá de simplemente almacenar agua. Y es que no sólo la almacena, sino que… ¡además la enfría! Y su potencial de enfriar es mayor cuanto más calor haga fuera.

La historia del mecanismo de un botijo

Esta historia pertenece a una persona con la que me siento muy identificado porque hizo lo que hago yo con muchas cosas que veo en la universidad. Resulta que en 1990 había un joven profesor español en la UPM llamado Gabriel Pinto que se sorprendió con una pregunta en un examen (presumiblemente de termodinámica o transmisión de calor): “Explique por qué se enfría el agua en un botijo”.

La típica curiosidad, fuera del temario pero relacionado con él, que el profesor explica en clase porque le parece interesante, y que acaba preguntando en el examen para ver quién estuvo atento ese día y asimiló conceptos.

Gabriel le estuvo dando vueltas al asunto y lo habló con otros compañeros. Se sabe que desde la antigüedad se han empleado botijos o vasijas de barro cocido poroso para almacenar agua porque la mantenía fresca. Unos decían que era porque la cerámica aísla mucho, y otros porque la cerámica indirectamente enfriaba el agua.

Y en esa última idea está la solución: el botijo enfría el agua de su interior.

Los materiales cerámicos son muy porosos, permitiendo intercambio de gases entre interior y exterior. Las capas más externas de agua, las que están en contacto con el aire, sufren de manera natural un proceso de evaporación. De esta manera, moléculas de agua en estado líquido rompen los enlaces que las mantienen unidas y pasan a estado gaseoso. La rotura física de estos enlaces implica haber realizado una fuerza o más bien un trabajo, o lo que es en parte lo mismo, una absorción de calor. De esta forma, al evaporarse el agua las moléculas que escapan lo hacen “robando” calor de la superficie del líquido, enfriándolo en su conjunto.

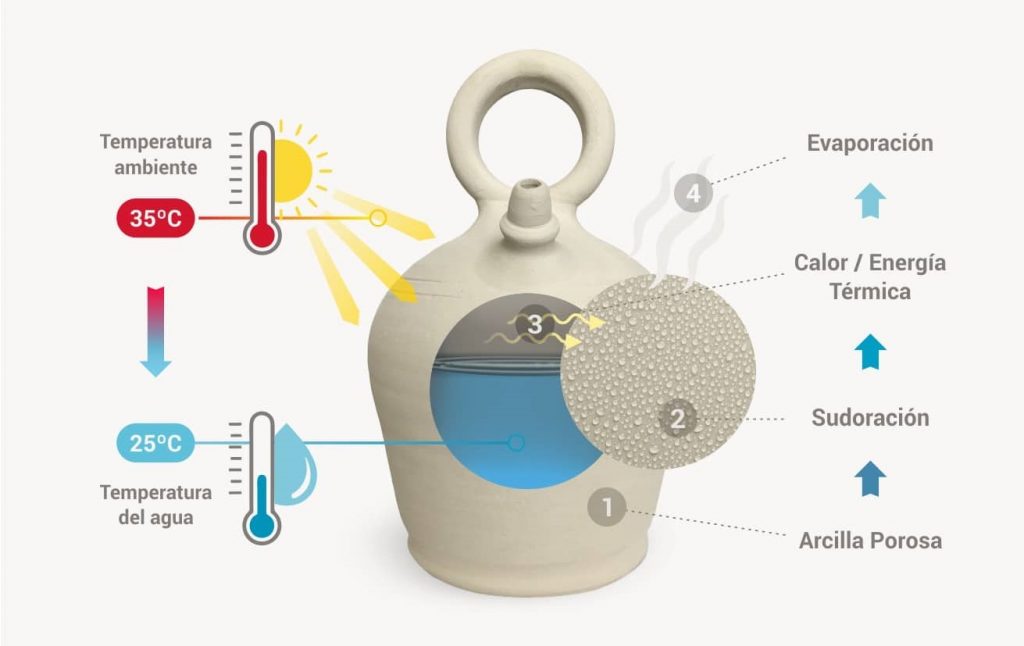
Este es el mecanismo que se produce con la sudoración, mediante la cual nos refrigeramos. Para más información acerca de cómo funciona este mecanismo lee este artículo interesante sobre el sudor. Pues bien, al igual que con el sudor, la capacidad de evaporación depende de dos factores:

• Humedad: A mayor humedad en las proximidades del líquido, más presencia de agua en estado gaseoso hay, y por lo tanto “no cabe tanto agua” y se dificulta la evaporación. Por eso en ambientes muy húmedos (jungla) se dice que sudas y estás siempre empapado y es agobiante, y por eso un ventilador que renueva el aire a tu alrededor te refresca a pesar de no estar enfriando el aire.
• Temperatura: A mayor temperatura, el agua se acerca más a su punto de ebullición y las moléculas cada vez tienen más tendencia a evaporarse (el punto de ebullición es la temperatura a la cual se rompen las cadenas forzosamente y todo el líquido se “evapora”).

El botijo, al estar abierto y ser poroso, permite la renovación del aire en su interior y reduce constantemente el nivel de humedad, facilitando la evaporación. Además, permite incluso la evaporación no sólo en su superficie en contacto con el aire, sino también en las zonas del líquido en contacto con la pared cerámica, aumentando enormemente la superficie de evaporación total.

Estos conceptos ya los manejaba Gabriel y se llevan estudiando desde que apareció la termodinámica. Esa es la gracia de hacer una pregunta general en un examen para afianzar o poner en práctica conceptos básicos (al fin y al cabo la ingeniería es eso).

Sin embargo, lo que nadie sabía a ciencia cierta era cuánto era capaz de enfriar un botijo. Revisó toda la literatura y contactó con diferentes expertos en la materia pero no encontró nada. Así, el curioso joven se propuso ser el que cuantificaría la capacidad de refrigeración de un botijo.

Tras comprar un botijo y el material necesario se puso a tomar medidas experimentales en el laboratorio (cómo iba variando la temperatura en función de distintos parámetros) y paralelamente materializaba sus observaciones por medio de la matemática, intentando desarrollar la ecuación diferencial por la cuál se regía este fenómeno.

Tuvo entonces que ayudarle un profesor más experimentado, José Ignacio Zubizarreta, quién solucionó una incongruencia en sus ecuaciones que hacía que el agua se enfriase indefinidamente tras evaporarse por completo.

Finalmente, presentaron un paper inédito en 1995 distribuido para todo el mundo en la revista estadounidense Chemical Engineering Education titulado An ancient method for cooling water explained by means of mass and heat transfer. Años más tarde, dos profesores de la Universidad de Valladolid, Andrés Martínez de Azagra y Jorge del Río, publicaron un artículo en el que se detalla un mapa mundial con zonas aptas para el uso de botijos.

Ecuaciones que rigen la capacidad de enfriamiento de un botijo

A continuación se presenta un resumen del paper que elaboraron en el que se detallan las ecuaciones empleadas y los resultados experimentales obtenidos.

El interior del botijo se modela como una esfera de radio \(R\) llena de agua dejando una cierta altura \(h\) libre como muestra la figura a continuación.

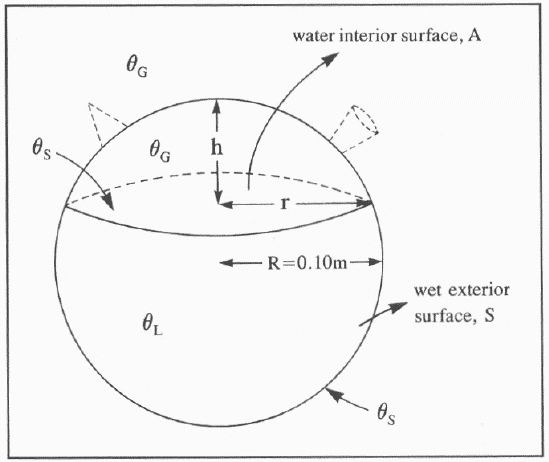
Se tiene que el volumen ocupado por el agua viene dado por la siguiente ecuación:

\(V=\dfrac{4}{3}\pi R^{3} – \dfrac{\pi}{3} \left (3 R h^{2} – h^{3} \right )\)

La superficie libre (superior) del agua \(A\) viene dada por:

\(A=\pi (2 R h – h^{2})\)

Y la superficie en contacto con la cerámica \(S\) es:

\(S=2 \pi R (2 R – h)\)

La temperatura externa es definida como \(\theta_{G}\), la temperatura de la superficie del agua como \(\theta_{S}\) y la temperatura media del agua como \(\theta_{L}\)

Se hacen a continuación las siguientes hipótesis o simplificaciones:

• El botijo es perfectamente esférico.
• La cerámica es perfectamente porosa y su permeabilidad es constante a lo largo de toda la superficie, permitiendo la formación de una capa uniforme y estable húmeda en la superficie exterior.
• No hay pérdida de agua adicional por goteo o derramamiento.
• El coeficiente de transmisión de materia entre las capas internas y externas es constante.
• La superficie de agua en contacto con aire se encuentra en equilibrio térmico.
• El aire se renueva constantemente y se mantiene a valores constantes de temperatura y humedad (fijado por las condiciones externas).
• El agua es completamente homogénea y presenta una densidad de 1 kg/L.
• La capacidad térmica de la cerámica y el aire es mucho más pequeña que la del agua, siendo despreciadas.

Las dos ecuaciones diferenciales que rigen por un lado la variación de volumen de agua y por otro lado la variación de temperatura son:

\(-\dfrac{dV}{dt} = k (A+S)(H_{S}-H)\)

\(V \cdot C_{P} \left (\dfrac{d\theta_{L}}{dt} \right ) = h_{c} (A+S) (\theta_{G} – \theta_{S}) + \\ + f \cdot \epsilon \cdot \sigma \left [ (273+ \theta_{G})^{4} – (273+ \theta_{S})^{4} \right ] (4 \pi R^{2} -S) – \\ – U (A+S) ( \theta_{L} – \theta_{S} ) – \lambda_{w} \left ( – \dfrac{dV}{dt} \right ) \)

La primera ecuación relaciona la disminución del volumen de agua con el ratio de evaporación del líquido tal que \(k\) es el coeficiente de transferencia de masa del agua por unidad de superficie y \( (H_{S}-H)\) la diferencia entre la humedad se saturación del aire y la humedad actual del aire. Los valores de las constantes dependen de las condiciones del experimento y se detallan en el paper.

La segunda ecuación es un análisis agrupado que expresa la variación térmica del líquido y corresponde a un balance entre entre la transmisión de calor del aire al agua (convección \(h_{c}\) y radiación térmica \(f \cdot \epsilon \cdot \sigma\) ), la pérdida de calor del líquido a la interfase líquida-gaseosa (medida por el coeficiente medio de transmisión de calor por unidad de área \(U\)) y la evaporación del agua (medido por el calor latente de evaporación \(\lambda_{w}\)).

Resultados experimentales y analíticos

Para poner en práctica estas ecuaciones y elaborar un experimento, fijaron parámetros. Se experimentó con un botijo esférico de radio 10 centímetros, en un ambiente cálido (aire exterior a temperatura \(\sigma_{G}\)=39 ºC con un 42% de humedad. Se introdujeron 3161 g de agua también a 39 ºC en el botijo y comenzó el experimento tomando mediciones de peso y temperatura cada ciertos instantes de tiempo.

Las gráficas a continuación muestran en línea continua la evolución teórica según las ecuaciones diferenciales y con puntos los valores experimentales medidos, observándose una gran conformidad.

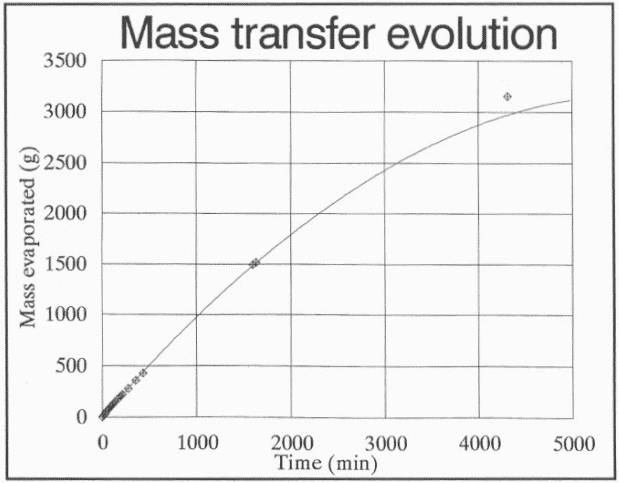
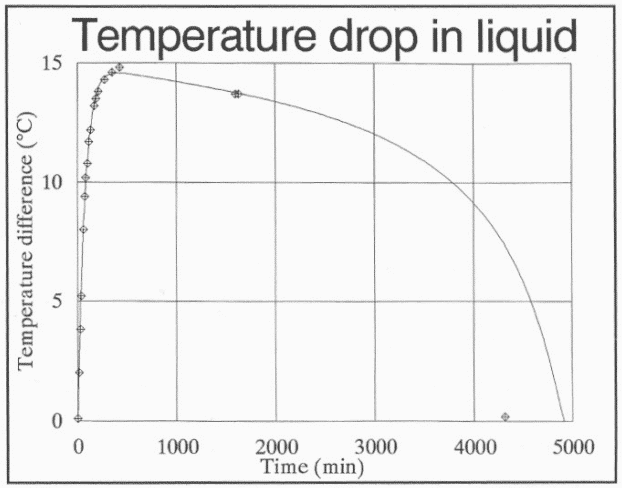
En las primeras 7 horas la temperatura disminuyó drásticamente hasta los 24ºC, con una pérdida de masa de 400g (aproximadamente un 12.5% de la masa inicial). Alrededor de 3 días después del inicio del experimento comienza un aumento primero progresivo y luego abrupto de la temperatura así como una rápida evaporación del agua. Finalmente, tras evaporarse todo el agua, la temperatura es de 39ºC de nuevo.

Estos resultados reflejaron la gran utilidad de un botijo y cómo es capaz de enfriar enormemente el agua de su interior en un día cálido. Obviamente, la utilidad de un recipiente de este tipo es limitada y por ello su uso se restringe realmente a darle un uso en el mismo día que se rellena.

A continuación os dejo una imagen térmica de un botijo con agua para que apreciéis la diferencia de temperatura con el entorno: