El Salto Hidráulico. Resaltos y número de Froude.

El salto hidráulico es un fenómeno de la hidráulica que se da en corrientes abiertas como ríos o aliviaderos. Este fenómeno consiste en el cambio abrupto en la altura y velocidad de un flujo que conlleva la generación de turbulencia y variación de las características del flujo.

¿Habéis observado alguna vez qué ocurre con el agua del grifo cuando cae en el fregadero? Seguro que sí. Y si no, ¡Ya estás tardando! Ese comportamiento se debe al salto hidráulico.

En este artículo comprenderemos por qué se produce este fenómeno, los parámetros de los que depende y su utilidad práctica.

Análisis de flujo ideal que pasa un obstáculo

Para descubrir el fenómeno del salto hidráulico, vamos a calcular matemáticamente la evolución de los parámetros de un flujo que pasa un obstáculo. De esta forma, nos haremos la idea de cómo evolucionan las características de un flujo cuando varía uno de sus parámetros (Velocidad o altura).

Vamos a considerar un flujo ideal y estacionario. Sin tener que dar más información acerca de la vorticidad del flujo, podemos emplear la ecuación de Bernoulli en la línea de corriente de la superficie.

Planteamos el problema: Una corriente de altura \(h_{1}\) y velocidad \(v_{1}\) conocidas fluye sobre un canal de elevación \(z_{1}\) conocido. Llegado a un punto, el canal pierde su elevación, y por lo tanto el flujo varía su altura y velocidad a unos valores \(h_{2}\) y \(v_{2}\) que queremos calcular.

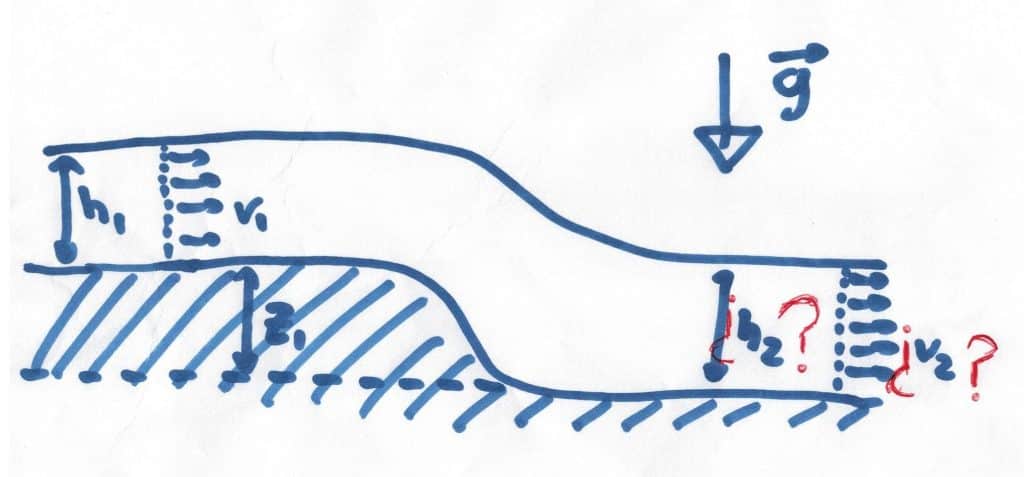
Para comenzar a resolver el problema, vamos a aplicar la ecuación de Bernoulli a la línea de corriente exterior:

\(\frac{1}{2} \rho \| \vec{u} \|^{2} + P+ \rho*g*z = cte\)

\(\frac{1}{2} \rho v_{1}^{2} + \underbrace{P_{1}}_{P_{a}} + \rho g (z_{1} + h_{1}) = \frac{1}{2} \rho v_{2}^{2} + \underbrace{P_{2}}_{P_{a}} + \rho g h_{2}\)

Empleando la ecuación de continuidad (Conservación de la masa):

\(\rho*v_{1}*h_{1}=\rho*v_{2}*h_{2}\)

Obtenemos el siguiente sistema de ecuaciones:

\(\left\{ \begin{matrix} \frac{1}{2} v_{1}^{2} + g (z_{1}+h_{1}) &=& \frac{1}{2} v_{2}^{2} + g h_{2} \\ v_{1} \cdot h_{1} &=& v_{2} \cdot h_{2} \end{matrix} \right.\)

2 ecuaciones y 2 incógnitas (\(h_{2}\) y \(v_{2}\)), fácil y sencillo para toda la familia… ¿No?

Pues efectivamente, no. Es un sistema de ecuaciones no lineal, ya que una de las incógnitas aparece al cuadrado. Esto hace que la solución no sea única. Para resolverlo despejamos el término \(h_{2}\) e igualamos.

\(\left\{ \begin{matrix} (1) & h_{2} &=& \frac{v_{1}^{2}}{2g} + z_{1} + h_{1} – \frac{v_{2}^{2}}{2g} \\ (2) & h_{2} &=& \frac{v_{1} \cdot h_{1}}{v_{2}} \end{matrix} \right.\)

Analíticamente obtenemos 3 soluciones. Vamos a hacer la gráfica de ambas ecuaciones de \(h_{2}(v_{2})\) para hacernos una idea de ellas:

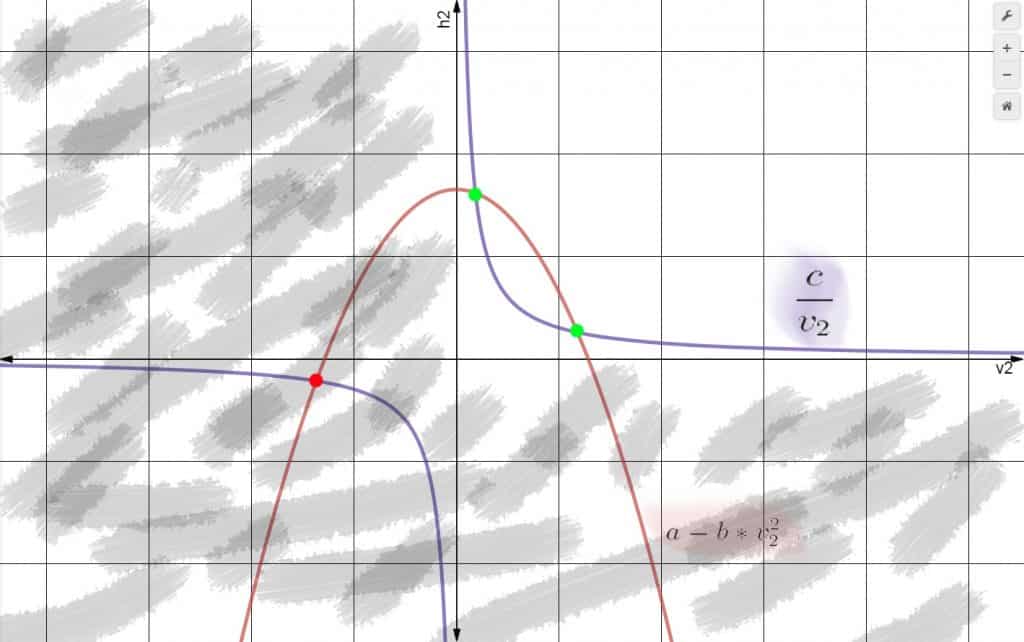
De las cuales únicamente aceptamos 2 posibles (Porque la tercera de ellas considera una velocidad negativa a altura negativa); Un flujo de gran altura y poca velocidad o un flujo de poca altura y gran velocidad. Pero… ¿Cómo podemos saber qué solución tomará nuestro flujo? Esta es la pregunta fundamental del artículo.

Análisis funcional. Número de Froude

Para poder analizar cuál puede ser la solución correcta a nuestro problema, vamos a realizar un análisis funcional sobre 2 funciones de valor constante que vamos a establecer; La función caudal Q(x) y la función Bernoulli B(x), que dependen ambas de una coordenada x que marca la posición en la que nos encontramos del canal.

La función Bernoulli no es más que la expresión funcional del término de Bernoulli. No incluirá la presión porque siempre será igual a la atmosférica a lo largo de la superficie libre.

\(Q(x)= \rho * U(x) * h(x) = \overline{Q}\)

\(B(x) = \frac{1}{2} \rho * U^{2}(x) + \rho * g *[h(x)+z(x)] = \overline{B}\)

Ambas funciones son constantes para todo x, de forma que sus derivadas son iguales a 0:

\(\frac{dQ}{dx} = \rho * U’ * h(x) +\rho * U * h’ = 0 \rightarrow \boxed{U’=-U * \frac{h’}{h}}\)

\(\frac{dB}{dx} = \rho * U*U’ + \rho * g * h’ + \rho * g * z’ = 0\)

Sustituyendo el término \(U’\) de la primera ecuación en la segunda para despejar \(h’\):

\(-U^{2} * \frac{h’}{h} + g * h’ + g * z’ = 0 \rightarrow \left [ \frac{U^{2}(x)}{g*h(x)}-1 \right ]*h'(x)=z'(x) \rightarrow\)

\(\rightarrow h'(x)=\frac{z'(x)}{\left [ \underbrace{\frac{U^{2}(x)}{g*h(x)}}-1 \right ]}\)

Definimos el número de Froude al cuadrado como la relación entre las fuerzas de inercia y las fuerzas de gravedad, es decir:

\(\boxed{\mathrm {Fr}^{2} = \frac{U^{2}}{g * h}}\)

Siendo h una longitud característica del problema.

\(\boxed{h'(x)=\frac{z'(x)}{\left [ \mathrm {Fr}^{2}-1 \right ]}}\)

Observamos que la evolución de la altura del flujo va a depender del cambio en el terreno y del número de Froude. El cambio del terreno es un parámetro arbitrario pero… ¿Qué es el número de Froude?

El número de Froude es un número adimensional que caracteriza el régimen de un flujo, de manera similar a como lo hace el número de Mach.

• Si Fr>1, el flujo es supercrítico
• Si Fr=1, el flujo es crítico
• Si Fr<1, el flujo es subcrítico

En función del Froude inicial y el tipo de cambio de terreno, existen 4 posibles casos, los cuales he plasmado en el siguiente dibujo:

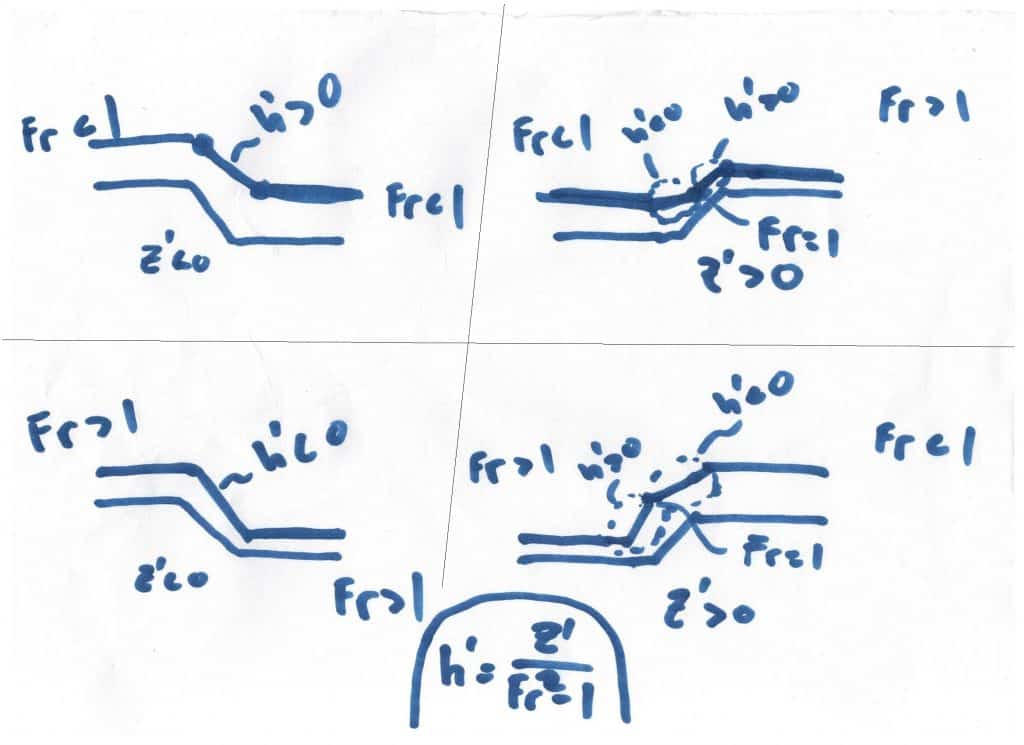
Pendiente negativa

En el caso de pendiente negativa, observamos que el caudal mantiene su tipo de flujo e incluso lo potencia aún más.

Este comportamiento puede observarse despejando el valor del Froude en función de las pendientes:

\(\mathrm {Fr}=\sqrt{\frac{z’+h’}{h’}}\)

En ambos casos z’ < 0

• Si h’>0, el cociente siempre va a dar un número inferior a 1 (Asumiendo que h’ es mayor que z’ u obtendríamos una raíz negativa)
• Si h'<0, el cociente siempre va a dar un número superior a 1

Pendiente positiva

En este caso el flujo cambia de tipo, existiendo un punto con Froude = 1, donde el flujo se denomina crítico y es el punto donde se produce la turbulencia.

En cualquier caso, para valores extremos de Froude (Muy pequeños/grandes) puede que la evolución del terreno no produzca un cambio en el tipo de flujo. Sin embargo, tenemos la certeza de que la evolución de la altura tras el resalto va a ser como lo describen las ecuaciones (Si inicia supercrítico disminuirá su velocidad, si inicia subcrítico aumenta su velocidad)

Aplicaciones del salto hidráulico

Una vez visto la variación de los parámetros de un flujo, vamos a ver las aplicaciones del salto hidráulico y tratar de comprender por qué se produce.

Salto hidráulico en grifo

Vamos a comenzar hablando del salto hidráulico que se produce cuando abrimos un grifo.

Al caer el agua, este se dirige de forma radial hacia el exterior. Debido a la energía que posee el flujo al caer, este adquiere una gran velocidad dentro de un pequeño espesor, siendo un flujo claramente supercrítico. A medida que el agua se aleja, su velocidad disminuye (Por pura conservación de la masa a medida que aumenta el radio debe de disminuir la velocidad).

Una vez que el flujo se ha ralentizado a una velocidad similar a la que se transmiten las ondas en el agua, el flujo puede recibir la “información” de que va demasiado rápido, y como si de una onda de choque se tratase, bruscamente se produce el salto hidráulico y el flujo pasa a subcrítico.

Control del oleaje y el caudal

Otro de los usos del salto hidráulico es el de controlar el movimiento del agua.

Tanto en las presas como en otro tipo de conductos, interesa que el agua fluya a un determinado caudal y sin demasiado oleaje. De lo contrario, el choque del agua con las paredes desgastaría los materiales y podría provocar una rotura de la estructura.

Del mismo modo, es necesario establecer algún tipo de barrera entre la playa y el paseo marítimo, de manera que en caso de una fuerte tormenta las olas no penetren en las edificaciones.

A continuación os presento un par de vídeos en los que se analiza cómo al añadir un obstáculo (Del mismo modo que hemos estudiado en este artículo) se induce un salto hidráulico que varía el flujo para adaptarse a nuestras necesidades.

Extra: Número de Froude y motricidad

El número de Froude no sólo se emplea en hidráulica, sino que su análisis es muy importante por ejemplo en el estudio de la motricidad.

El número de Froude puede ser empleado para estudiar los patrones de movimiento de los animales. Para analizar el movimiento de una extremidad, se modela un péndulo invertido cuyo “péndulo” es la articulación y el centro de giro el pie o punto de apoyo.

El número de Froude se establece como el cociente entre la fuerza centrífuga (Velocidad de movimiento de la extremidad) y la fuerza de gravedad (Con longitud característica igual a la extremidad).

\({\displaystyle \mathrm {Fr} ={\frac {\text{Fuerza centrifuga}}{\text{Fuerza gravitacional}}}={\frac {\;{\frac {mv^{2}}{l}}\;}{mg}}={\frac {v^{2}}{gl}}}\)

Tomando como longitud característica la extremidad, el valor máximo del número de Froude se situaría en 1, ya que un valor superior supondría el “despegue” de la extremidad y la consecuente separación del pie del suelo.

En humanos y pájaros empíricamente se ha demostrado que la transición natural entre andar y correr ocurre siempre con un Froude muy cercano a 0,5

Este es uno de los múltiples ejemplos que nos muestra la transversalidad de las ciencias y cómo por ejemplo para analizar el movimiento de un ser humano se mezcla el estudio de un péndulo (Mecánica) con el número de Froude (Hidráulica).

Si te gustaría obtener más información acerca de la motricidad y el número de Froude, aquí encontrarás un artículo acerca de ello.