El Principio de Arquímedes, junto con el Teorema de Pitágoras, es uno de los “teoremas” que a la mayoría de la gente le vendría a la mente en caso de tener que enunciar uno de memoria.
Como sabréis, este principio nos indica el valor de la fuerza que se ejerce sobre un cuerpo que se encuentra inmerso en un fluido y que lo permite flotar.
En este artículo veremos matemáticamente cómo se obtiene el valor de dicha fuerza, y para ello deberemos de deducir la ecuación básica de la hidrostática.
Concepto de fluido y de hidrostática
Un fluido (Líquido o gas) se define como una sustancia que se deforma de manera continua ante la acción del más pequeño esfuerzo tangencial, o dicho de otra manera, una sustancia incapaz de resistir esfuerzos tangenciales sin deformarse.
Cuando un fluido se encuentra en reposo, por pura definición, el único tipo de fuerzas que actúan sobre él son esfuerzos normales. Decimos en este caso que nuestro problema se basa en hidrostática (Fluido-quieto).
Obtención fórmula de la hidrostática
Para que una partícula del fluido se encuentre en reposo, debe de existir un equilibrio de fuerzas. Vamos a considerar un volumen infinitesimal de fluido:
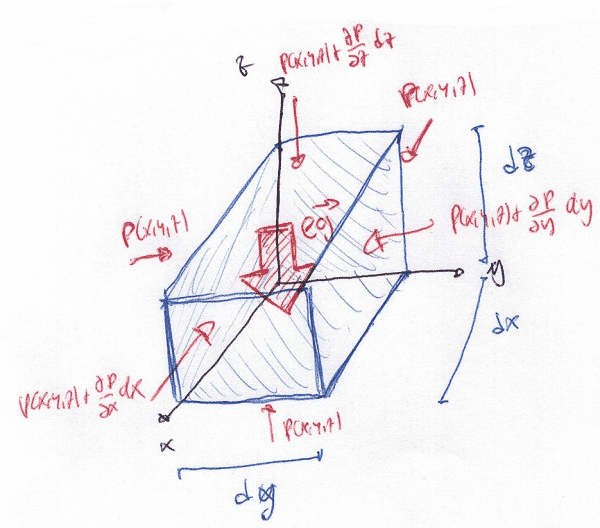
Tomaremos como valor \(P(x,y,z)\) a las presiones o esfuerzos normales ejercidos sobre las caras ocultas del volumen, y obtendremos una aproximación del incremento infinitesimal de presión que actúa sobre las caras visibles empleando una linearización \(P(x,y,z)+\frac{\partial P(x,y,z)}{dx_{i}} \delta x_{i}\).
Además, situando la partícula con el eje z paralelo a la gravedad, situamos la fuerza volumétrica \(\rho g\) hacia abajo.
Vamos a realizar un equilibrio de fuerzas en los 3 ejes:
\(x : P(x,y,z)dydz – (P(x,y,z)+\frac{\partial P(x,y,z)}{\partial x} dx)dydz=0 \iff \frac{\partial P(x,y,z)}{\partial x}=0 \\\) \(y : P(x,y,z)dxdz – (P(x,y,z)+\frac{\partial P(x,y,z)}{\partial y} dy)dxdz=0 \iff \frac{\partial P(x,y,z)}{\partial y}=0 \\\) \(z : P(x,y,z)dxdy – (P(x,y,z)+\frac{\partial P(x,y,z)}{\partial z} dz)dxdy – \rho g *dxdydz=0 \iff \\\) \( \iff \dfrac{\partial P(x,y,z)}{\partial z}=-\rho g \\\)Es decir, tenemos las siguientes ecuaciones diferenciales de \(P(x,y,z)\):
\(\left\{ \begin{aligned} \frac{\partial P(x,y,z)}{\partial x} &= 0 \\ \frac{\partial P(x,y,z)}{\partial y} &= 0 \\ \frac{\partial P(x,y,z)}{\partial z} &= -\rho g \\ \end{aligned} \right. \)
La presión no depende de x ni de y. La solución general del campo de presiones \(P(x,y,z)\) es:
\(P=P(z)=-\rho gz + P_{o} \rightarrow P(z)= P_{o} – \rho g z \) , siendo \(P_{o}\) una presión de referencia dada en z=0 (Dato dado como condición de contorno).
Si tomamos como valor de referencia la presión atmosférica que se encuentra a una altura z=0, la variación lineal de la presión vendrá dada por:
\(P(z)= P_{atm} – \rho g z \)
De manera que si nos sumergimos, la presión aumenta (z toma valores negativos). En cambio, si ascendemos, la presión disminuye
{Si tomamos el z=0 en la superficie de un fluido, para poder estudiar la evolución de la presión en el aire no podemos simplemente tomar valores positivos de z. Debemos de actualizar el valor de la densidad \(\rho\) al valor de la densidad del fluido en el que nos movemos. (\(P(z)= P_{o} – \rho_{aire} g z \))
{Al integrar respecto de z hemos asumido que la densidad es constante en todo el campo fluido. En caso de tener por ejemplo un fluido con densidad variable en función de la temperatura (Cuya distribución a su vez dependerá de la coordenada z debido a la convección), deberíamos de aplicar una aproximación a la dependencia de la densidad para poder integrarla (Por ejemplo la Aproximación de Boussinesq)
Demostración del Principio de Arquímedes
El Principio de Arquímedes dice lo siguiente:
“Todo cuerpo sumergido en un fluido experimenta una fuerza vertical hacia arriba igual al peso del volumen del fluido que desaloja”
Nos da la clásica fórmula de empuje \(E=\rho_{fluido} * V_{sumergido} * g \)
Vamos a demostrar matemáticamente dicho Principio empleando únicamente la hidrostática.
Comenzamos tomando un cuerpo de volumen indefinido V que se encuentra parcialmente sumergido en un fluido de densidad \(\rho\).
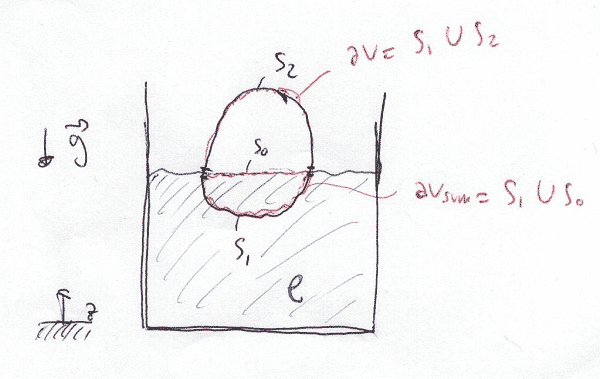
Nuestro campo de presiones presenta la siguiente ditribución:
\(P(z) = \begin{cases} P_{o} – \rho_{\text{aire}} gz, & z > 0 \\ P_{o} – \rho g z, & z < 0 \end{cases}\)(Asumimos la presión constante en z>0 debido a la baja densidad del aire, considerando \(P_{o}=P_{atm}\))
Sobre el cuerpo actuarán 2 fuerzas, las cuales lo colocan en equilibrio; La fuerza hacia abajo, provocada por la fuerza volumétrica de la gravedad, y la fuerza de empuje de arquímedes que tiene naturaleza superficial y se debe a la distribución de presiones en la superficie del cuerpo (Abajo hay más presión que arriba, por lo que el cuerpo sufre una fuerza hacia arriba)
Vamos a calcular la resultante de los esfuerzos superficiales como:
\(\displaystyle \vec{R}= \int_{\partial V} \vec{t_{n}} dA = -\oint_{\partial V} P * \vec{n} dA =\)El signo (-) lo colocamos porque la fuerza de presión actúa normal a la superficie pero con signo opuesto a la normal exterior \(\vec{n}\)
\(=\displaystyle -\int_{S_{1}} P(z) * \vec{n} dA -\int_{S_{2}} P(z) * \vec{n} dA = \\\) \(\displaystyle -\int_{S_{1}} (P_{o}-\rho g z) * \vec{n} dA -\int_{S_{2}} P_{o} * \vec{n} dA = \\\) \(\displaystyle -\oint_{\partial V} P_{o} * \vec{n} dA +\int_{S_{1}} \rho g z * \vec{n} dA \rightarrow \vec{R}=\int_{S_{1}} \rho g z * \vec{n} dA \\\)Hemos aplicado el teorema de la divergencia de Gauss en la integral cerrada de superficie obteniendo un valor nulo (Divergencia de un vector constante es 0)
Tomamos como superficie \(S_{o}\) la superficie que coincide con la sección del cuerpo flotando que pasa justo por la entrefase líquido-aire y sumamos/restamos la fuerza que ejerce debido a la presión local:
\(\displaystyle \int_{S_{1}} \rho g z * \vec{n} dA = \int_{S_{1}} \rho g z * \vec{n} dA + \int_{S_{o}} \rho g z * \vec{n} dA -\int_{S_{o}} \rho g z * \vec{n} dA = \\ \) \(= \displaystyle \oint_{\partial V_{sum}} \rho g z * \vec{n} dA – \int_{S_{o}} \rho g (z=0) * \vec{n} dA \rightarrow \\\)\(\displaystyle \rightarrow\vec{R}=\oint_{\partial V_{sum}} \rho g z * \vec{n} dA\) , siendo \(\partial V_{sum}\) la superficie cerrada del volumen que se encuentra sumergido.
Aplicando de nuevo el teorema de la divergencia de Gauss a dicha integral cerrada:
\(\displaystyle \oint_{\partial V_{sum}} \rho g z * \vec{n} dA = \rho g \int_{V_{sum}} \vec{k}{(\vec{\nabla}z)} dV = \rho g \vec{k} \int_{V_{sum}} dV = \rho g V_{sum}\vec{k} \\ \)Se demuestra que la resultante es \( \vec{R}=\rho g V_{sum}\vec{k}\)
Que coincide con el enunciado del Principio de Arquímedes.
El cálculo del volumen que se sumerge es tan fácil como hacer un equilibrio de fuerzas:
\(\rho_{cuerpo}V_{total}g=\rho_{fluido}V_{sumergido}g\)\(V_{sumergido}=\frac{\rho_{cuerpo}}{\rho_{fluido}}V_{total}\)
Una vez conocidos todos los detalles del Principio de Arquímedes os pregunto… Si un hielo se encuentra flotando en un vaso de agua y este se derrite… ¿Aumentará el volumen de agua? La respuesta y el análisis se encuentra en el siguiente artículo:
4 comentarios en «Demostración matemática del Principio de Arquímedes»