El método de Vortex Lattice (Vortex Lattice Method (VLM)) es un método numérico empleado en mecánica de fluidos computacional (CFD) principalmente en las primeras etapas de diseño de aeronaves y en la aerodinámica a nivel universitario.
Dicho método consiste en modelar las superficies de sustentación como una hoja infinitamente delgada compuesta de vórtices discretos que permiten obtener una solución numérica al movimiento del flujo alrededor del perfil. Como consecuencia, puede obtenerse una distribución de presiones que permite el cálculo de la sustentación y el momento aerodinámico.
Sin embargo, para poder emplear dicho método deben darse unas condiciones que permitan despreciar el espesor del perfil y la viscosidad del flujo. Como consecuencia, no permite calcular la resistencia aerodinámica. No obstante es un método muy empleado porque numéricamente es muy liviano y permite estimar con precisión y rapidez coeficientes tan importantes como el de sustentación que permiten tomar decisiones en la fase de diseño preliminar.
En este artículo va a analizarse dicho método para un perfil bidimensional. Gran parte del desarrollo teórico y las imágenes son extraídas de los apuntes de la asignatura Aeroelasticidad de Miguel Pérez-Saborid Sánchez-Pastor elaborados por Álvaro Jiménez Aires.
Ecuaciones generales
Considérese un perfil aerodinámico bidimensional como el de la siguiente figura en el seno de una corriente incidente con velocidad \(U_{\infty}\), densidad \(\rho_{\infty}\) y presión \(p_{\infty}\) inclinado un cierto ángulo \(\alpha(t)\).

La cuerda del perfil es \(c\) y las funciones \(z_{i}(x,t)\) y \(z_{e}(x,t)\) representan la curva de intradós y extradós respectivamente. Se supone que el perfil es rígido y esbelto, es decir, que no se deforma (espesor siempre constante) y que es mucho más delgado que alargado. Dichas condiciones se resumen matemáticamente con:
\(z_{e}(x,t)-z_{i}(x,t) = e(x) \ll c\)
Además, se supone que el ángulo que el perfil forma con la corriente incidente \(\alpha(t)\) es pequeño, es decir:
\(\dfrac{\partial z_{e}(x,t)}{\partial x} \sim\dfrac{\partial z_{i}(x,t)}{\partial x} \ll 1\)
Asimismo se considera que la velocidad de desplazamiento vertical del perfil es pequeña comparada con la velocidad incidente de la corriente:
\(\dfrac{\partial z_{e}(x,t)}{\partial t} =\dfrac{\partial z_{i}(x,t)}{\partial t} \ll U_{\infty}\)
Nótese que ambas derivadas son idénticas debido a la condición de perfil rígido:
\(\dfrac{\partial z_{e}(x,t)}{\partial t} =\dfrac{\partial z_{i}(x,t)}{\partial t} + \dfrac{\partial e(x)}{\partial t} = \dfrac{\partial z_{i}(x,t)}{\partial t} \)
En cuanto al flujo incidente, se supondrá que el número de Reynolds es muy grande:
\(Re = \dfrac{\rho_{\infty} U_{\infty} c}{\mu_{\infty}} \gg 1\)
Esto se da cuando el número de Reynolds toma valores del orden de \(10^{6}\). Esto nos permite asumir que los efectos viscosos están confinados en capas límites muy estrechas, adyacentes a la superficie y en la estela de espesor característico proporcional a:
\(\dfrac{\delta_{v}}{c} \sim \dfrac{\delta_{E}}{c} \sim \dfrac{1}{\sqrt{Re}} \ll 1\)
Y que, de acuerdo con las hipótesis anteriores, se considera que no hay desprendimiento de la capa límite en ningún momento. Por lo tanto, el flujo exterior, que determina la distribución de presiones en el perfil, será poco perturbado. Matemáticamente puede considerarse el flujo inicial al que se le suma una perturbación:
\(\vec{v}(x,z,t) = U_{\infty} \vec{e}_{x} + \vec{v}'(x,z,t) \)
\(p(x,z,t) = p_{\infty} + p'(x,z,t)\)
Donde \(\vec{v}'(x,z,t) \) es la velocidad perturbada:
\(\vec{v}'(x,z,t) = v’_{x} (x,z,t)\vec{e}_{x} + v’_{z}(x,z,t) \vec{e}_{z}\)
Cabe recalcar el hecho de que son perturbaciones, es decir, que \(\| \vec{v}’ \| \ll U_{\infty}\) y \( p’ \ll p_{\infty}\).
Por último se asume que el número de Mach es inferior a 0.3 y, por lo tanto, puede considerarse el flujo como incompresible tal que \(\rho \approx \rho_{\infty}\). Además, el número de Froude es elevado por lo que las fuerzas de inercia son muy superiores a las de gravedad y estas últimas pueden despreciarse.
\(M_{\infty} = \dfrac{U_{\infty}}{\sqrt{\gamma \ p_{\infty}/\rho_{\infty}}} < 0.3\)
\(F^{2}_{r} = \dfrac{U^{2}_{\infty}}{gc} \gg 1\)
Tras realizar todas las hipótesis anteriores, las ecuaciones de Navier-Stokes simplificadas definen el comportamiento del fluido:
\(\nabla \cdot \vec{v} = 0\) \(\rho_{\infty} \dfrac{\partial \vec{v}}{\partial t} + \rho_{\infty} (\vec{v} \cdot \nabla) \cdot \vec{v} = -\nabla p\)Sustituyendo \(\vec{v}(x,z,t) = U_{\infty} \vec{e}_{x} + \vec{v}'(x,z,t) \) y \(p(x,z,t) = p_{\infty} + p'(x,z,t)\) teniendo en cuenta que los términos constantes desaparecen en la derivada y que \(U_{\infty} \gg \|\vec{v}’\|\), las ecuaciones resultan simplificadas en términos de las cantidades perturbadas:
\(\boxed{\nabla \cdot \vec{v}’ = \dfrac{\partial v_{x}’}{\partial x} + \dfrac{\partial v_{z}’}{\partial z} = 0} \\\) \(\rho_{\infty} \dfrac{\partial \vec{v}’}{\partial t} + \rho_{\infty} (U_{\infty} \vec{e}_{x} \cdot \nabla) \cdot \vec{v}’ = -\nabla p’ \\\)Como \(\vec{e}_{x} \cdot \nabla = \partial / \partial x\), la ecuación del momento puede escribirse como:
\(\boxed{\rho_{\infty} \dfrac{\partial \vec{v}’}{\partial t} + \rho_{\infty} U_{\infty} \dfrac{ \partial \vec{v}’}{\partial x} = -\nabla p’}\)Dicha ecuación en principio no deja nada en claro. Sin embargo, si aplicamos el rotacional a todos los términos de la ecuación sabiendo que podemos conmutar rotacional con derivada parcial temporal y espacial así como que el rotacional de un gradiente es nulo:
\(\nabla \times \dfrac{\partial (\bullet)}{\partial t} = \dfrac{\partial (\nabla \times (\bullet))}{\partial t} \\\) \(\nabla \times \dfrac{\partial (\bullet)}{\partial x} = \dfrac{\partial (\nabla \times (\bullet))}{\partial x} \\\) \(\nabla \times \nabla (\bullet) = 0 \)La última ecuación queda finalmente como:
\(\rho_{\infty} \dfrac{\partial (\nabla \times \vec{v}’)}{\partial t} + \rho_{\infty} U_{\infty} \dfrac{\partial (\nabla \times \vec{v}’)}{\partial x} = 0 \)
El operador \(\dfrac{\partial}{\partial t} + U_{\infty} \dfrac{\partial}{\partial x}\) en este contexto representa la derivada material, por lo que la ecuación se resume en:
\(\boxed{\rho_{\infty} \dfrac{D (\nabla \times \vec{v}’)}{Dt} = 0}\)
Dicha ecuación implica que la cantidad \(\nabla \times \vec{v}’\) permanece constante para cualquier observador que se mueve con la velocidad del fluido \(U_{\infty} \vec{e}_{x}\).
En el infinito, al estar hablando de una magnitud de perturbación, esta tomará un valor nulo, siendo entonces \(\nabla \times \vec{v}’ = 0\) en \(x \rightarrow -\infty\). Por lo tanto, la corriente se desplazará mantieniendo dicho valor nulo por lo que su valor en cualquier punto (x,z) resulta nulo \(\nabla \times \vec{v}’=0\).
En consecuencia, \(\vec{v}’\) deriva de un potencial, denominado potencial de velocidad de perturbación:
\(\vec{v}'(x,z,t) = \nabla \phi(x,z,t)\)
La ecuación de cantidad de movimiento en la dirección \(x\) queda, sustituyendo la velocidad por el potencial:
\(\rho_{\infty} \dfrac{\partial^{2} \phi}{\partial t \partial x} + \rho_{\infty} U_{\infty} \dfrac{ \partial v_{x}’}{\partial x} = -\dfrac{\partial p’}{\partial x} \rightarrow \dfrac{\partial}{\partial x} \left ( \rho_{\infty} \dfrac{\partial \phi}{\partial t } + \rho_{\infty} U_{\infty} v_{x}’ + p’ \right ) = 0 \iff\) \( \iff \rho_{\infty} \dfrac{\partial \phi}{\partial t } + \rho_{\infty} U_{\infty} v_{x}’ + p’ = cte = 0\)Dicha ecuación resulta \(0\) puesto que al ser la derivada nula, la ecuación debe ser constante. En el infinito tanto la velocidad como la presión perturbada son nulas, por lo que la constante es igual a \(0\).
De esta forma podemos calcular el valor de la presión perturbada como:
\( p'(x,z,t) = -\rho_{\infty} \dfrac{\partial \phi (x,z,t)}{\partial t } – \rho_{\infty} U_{\infty} v_{x}'(x,z,t)\)
Ecuación y condiciones de contorno
En resumen, de las ecuaciones de Navier-Stokes hemos llegado a las siguientes ecuaciones:
\(\nabla \times \vec{v}’ = 0 \rightarrow \vec{v}’= \nabla \phi \\\) \(\nabla \cdot \vec{v}’ = 0 \rightarrow \boxed{\nabla^{2} \phi = 0} \\\)Es decir, que se comprimen en una ecuación: La ecuación de Laplace. Esta es una ecuación en derivadas parciales de segundo orden de tipo elíptico. Dicha ecuación es muy importante puesto que aparece en casi todas las ramas de la física con frecuencia.
Tiene infinitas soluciones, siendo cada una de ellas denominada como una función armónica. Pero dejando el análisis matemático a un lado, nuestro objetivo será el siguiente: elegir arbitrariamente una función armónica (que, por lo tanto, cumpla la ecuación), y elegirla tal que cumpla con las condiciones de contorno del problema, de forma que dicha función sea válida para representar el campo de velocidades de perturbación.
Condiciones de contorno en el infinito
En puntos muy alejados del perfil la velocidad de perturbación será nula. Por lo tanto, la ecuación matemática que la función deberá cumplir es:
\(\boxed{\|\vec{v}’\| \rightarrow 0} \ en\ \|x\| \rightarrow \infty\)
Condiciones de contorno en el perfil
Como estamos considerando un flujo ideal, la condición de contorno de contacto entre fluido-sólido no será la de movimiento relativo nulo sino que se relaja a simplemente movimiento relativo normal nulo. Esto físicamente se refiere a que el flujo se mueve por una línea de corriente que coincide en todo momento con la superficie del perfil, pudiendo existir velocidad relativa tangente.
Habrá por un lado un componente de velocidad asociado a la impenetrabilidad del perfil. Imaginemos un perfil que no se desplaza sino que se mantiene fijo. El perfil presentará una curvatura o ángulo de ataque tal que la pendiente que ve el flujo en un determinado punto del perfil en el extradós/intradós vendrá dada por \( \dfrac{\partial z_{e,i}}{\partial x}\). Considerando un perfil delgado y situándolo a lo largo del eje z la componente de velocidad debida a la impenetrabilidad resulta:
\(v_{z_{imp}}'(x,0^{\pm},t) = U_{\infty} \dfrac{\partial z_{e,i}}{\partial x}\)
Por otra parte como el movimiento no es estacionario el perfil también se estará moviendo y oscilando verticalmente. Este movimiento imprime una cierta velocidad de arrastre al flujo tal que la componente resulta:
\(v_{z_{arr}}'(x,0^{\pm},t) = \dfrac{\partial z_{e,i}}{\partial t}\)
Sumando ambas contribuciones, la condición de contorno en el perfil resulta:
\(\boxed{v_{z}’ (x,0^{\pm},t) =v_{z_{arr}}’ + v_{z_{imp}}’ = \dfrac{\partial z_{e,i}}{\partial t} + U_{\infty} \dfrac{\partial z_{e,i}}{\partial x} }\ en \ 0 \leq x \leq c\)
Condiciones de contorno en la estela
La estela se considera de espesor nulo y por lo tanto ni acumula masa ni aguanta una diferencia de presiones.
Como no acumula masa, la velocidad vertical del intradós debe ser igual a la velocidad vertical del extradós, o lo que es lo mismo:
\(\boxed{v_{z}’ (x,0^{-},t) = v_{z}’ (x,0^{+},t)}\ en \ x \geq c\)
Recordemos que la presión perturbada viene dada por:
\( p'(x,z,t) = -\rho_{\infty} \dfrac{\partial \phi (x,z,t)}{\partial t } – \rho_{\infty} U_{\infty} v_{x}'(x,z,t)\)
Como la diferencia de presiones en la estela es nula, debe verificarse que \(p'(x,0^{-},t) – p'(x,0^{+},t) = 0 \).
Es decir, que se tiene que:
\( \rho_{\infty} \dfrac{\partial }{\partial t } \left \{ \phi (x,0^{+},t) – \phi (x,0^{-},t) \right \} – \rho_{\infty} U_{\infty} \left \{v_{x}'(x,0^{+},t) – v_{x}'(x,0^{-},t) \right \} = 0\)
Esta ecuación se puede escribir convenientemente en términos de la circulación \(\Gamma\) y la densidad de circulación \(\gamma\).
La circulación alrededor de un segmento limitado por los puntos O-A viene dada por:
\(\displaystyle \Gamma = \oint \vec{v} \cdot d\vec{l} = \int_{O}^{A} \vec{v}(x,0^{+},t) \cdot d\vec{l} + \int_{A}^{O} \vec{v}(x,0^{-},t) \cdot d\vec{l} =\)
\(=\displaystyle \int_{O}^{A} (\vec{v}(x,0^{+},t) – \vec{v}(x,0^{-},t) ) \cdot d\vec{l} \)
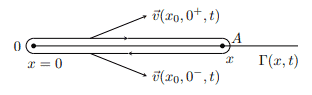
Como la velocidad \(\vec{v}\) hemos dicho que es \(\vec{v} = U_{\infty} \vec{e}_{x} + \vec{v}’\) y el diferencial de longitud, al ser un segmento en el eje x, resulta \(d\vec{l} = dx_{0} \vec{e}_{x}\) siendo \(dx_{0}\) una variable muda que recorre el intervalo \([0,x]\), la circulación resulta:
\(\Gamma(x,t) =\displaystyle \int_{0}^{x} \left(v(x_{0},0^{+},t) – v(x_{0},0^{-},t) \right ) \cdot dx_{0} \)
Que, si sustituimos el potencial de velocidad \(\dfrac{\partial \phi}{\partial x} = v_{x}’\) podemos expresar la integral como:
\(\Gamma(x,t) =\displaystyle \int_{0}^{x} \dfrac{\partial}{\partial x_{0}} \left(\phi(x_{0},0^{+},t) – \phi(x_{0},0^{-},t) \right ) \cdot dx_{0} \)
Y, en base al Teorema Fundamental del Cálculo (teniendo en cuenta que para \(x=0\) la diferencia de los potenciales es nula al considerar dicho punto anterior al borde de ataque), obtenemos la circulación en términos del potencial tal que:
\(\Gamma(x,t) = \phi(x,0^{+},t) – \phi(x,0^{-},t)\)
La densidad de circulación \(\gamma(x,t)\) se define como la circulación por unidad de longitud, es decir, tal que:
\(\gamma(x,t) = \dfrac{\partial \Gamma(x,t)}{\partial x} = v(x,0^{+},t) – v(x,0^{-},t)\)
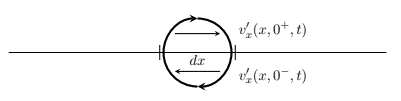
Escribiendo la ecuación de las presiones en términos de la circulación y su densidad que justo acabamos de definir, la ecuación resulta:
\(\dfrac{\partial \Gamma (x,t)}{\partial t} + U_{\infty} \cdot \gamma(x,t) = 0\)
Si dicha ecuación la derivamos con respecto a x, llegamos a un resultado sorprendente:
\(\boxed{\dfrac{\partial \gamma (x,t)}{\partial t} + U_{\infty} \cdot \dfrac{\partial \gamma(x,t)}{\partial x} = \dfrac{D \gamma_{E}(x,t)}{Dt} =0} \ en \ x \geq c\)
La densidad de circulación en la estela se escribe como \(\gamma_{E}\) para resaltar que dicha ecuación sólo se cumple para la densidad de circulación en la estela. Físicamente representa que, para un espectador que se mueve con velocidad \(U_{\infty} \vec{e}_{x}\), la densidad de circulación que experimenta es constante. Esto podría entenderse como que en la estela se forma un torbellino de un determinado valor de densidad de circulación y este torbellino se desplaza con la corriente manteniendo su intensidad constante.
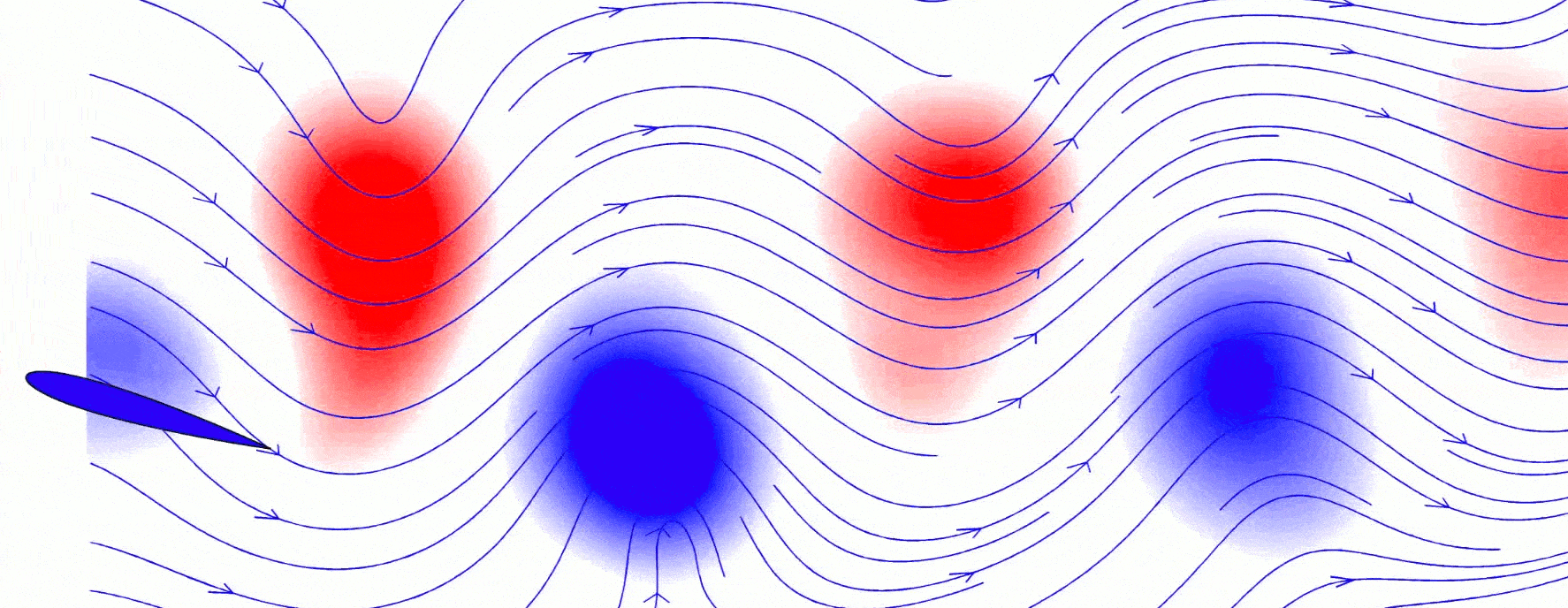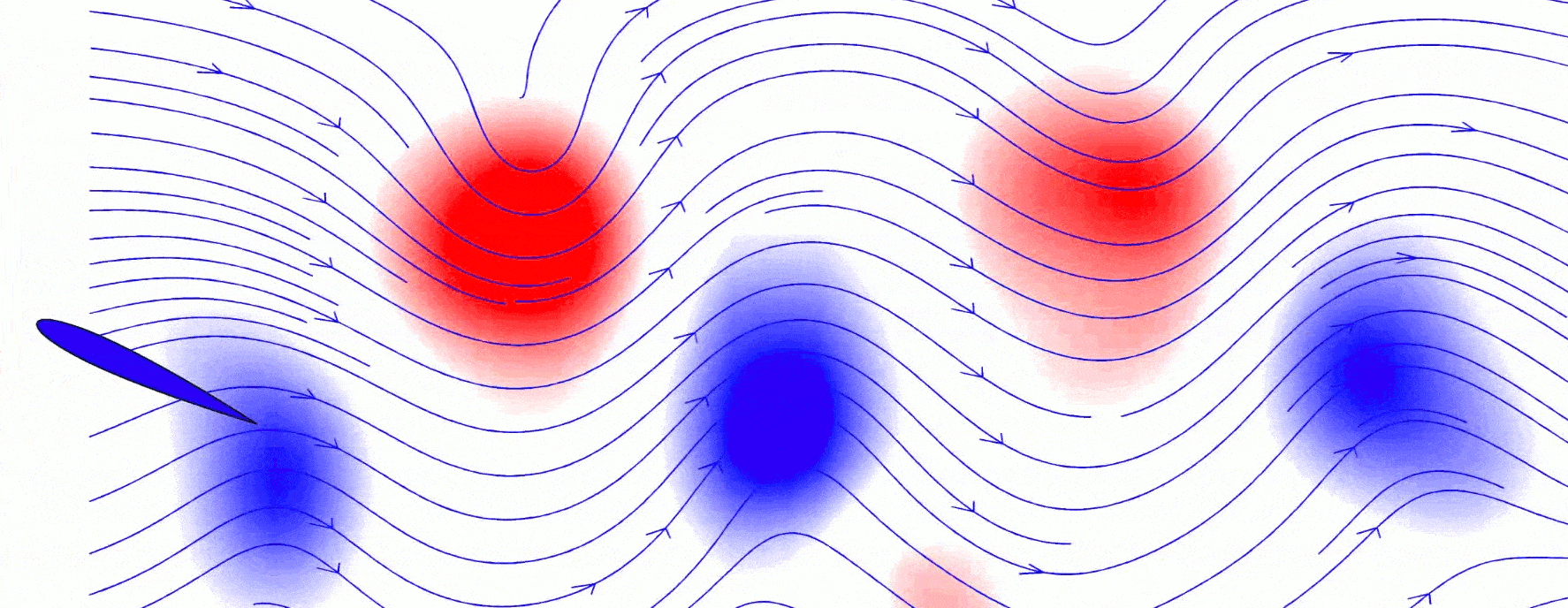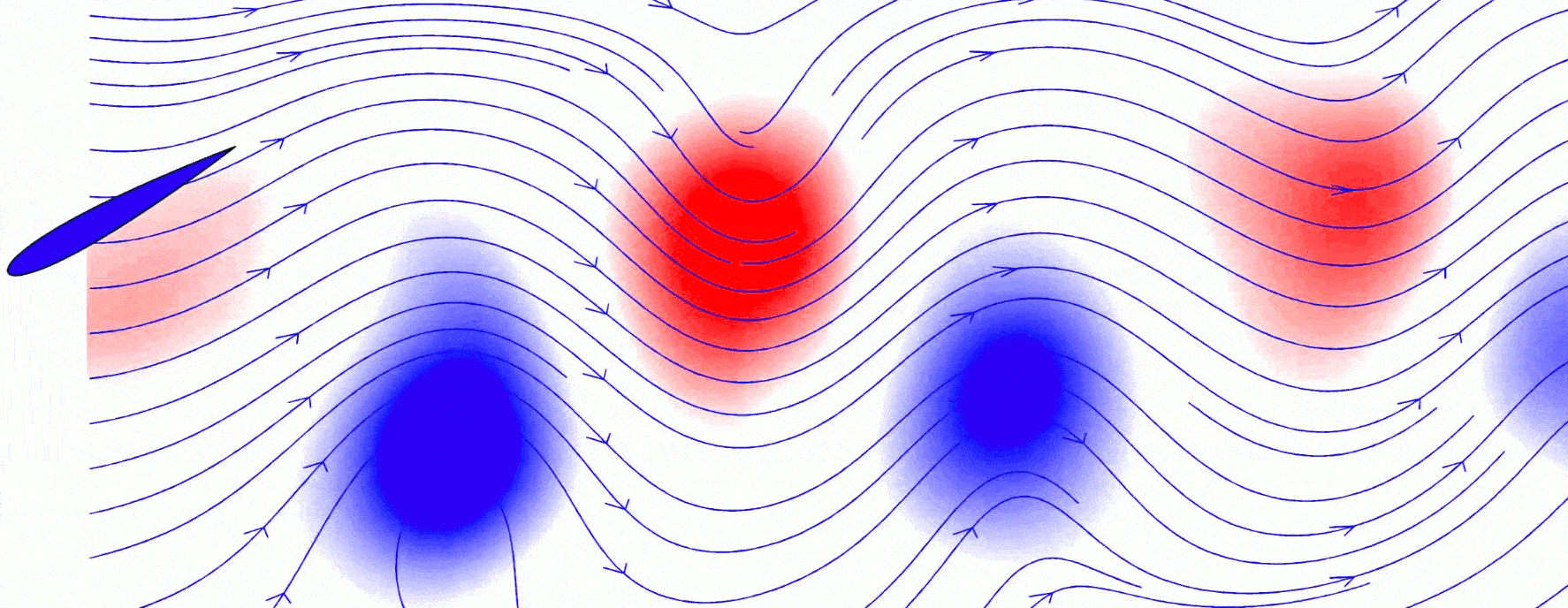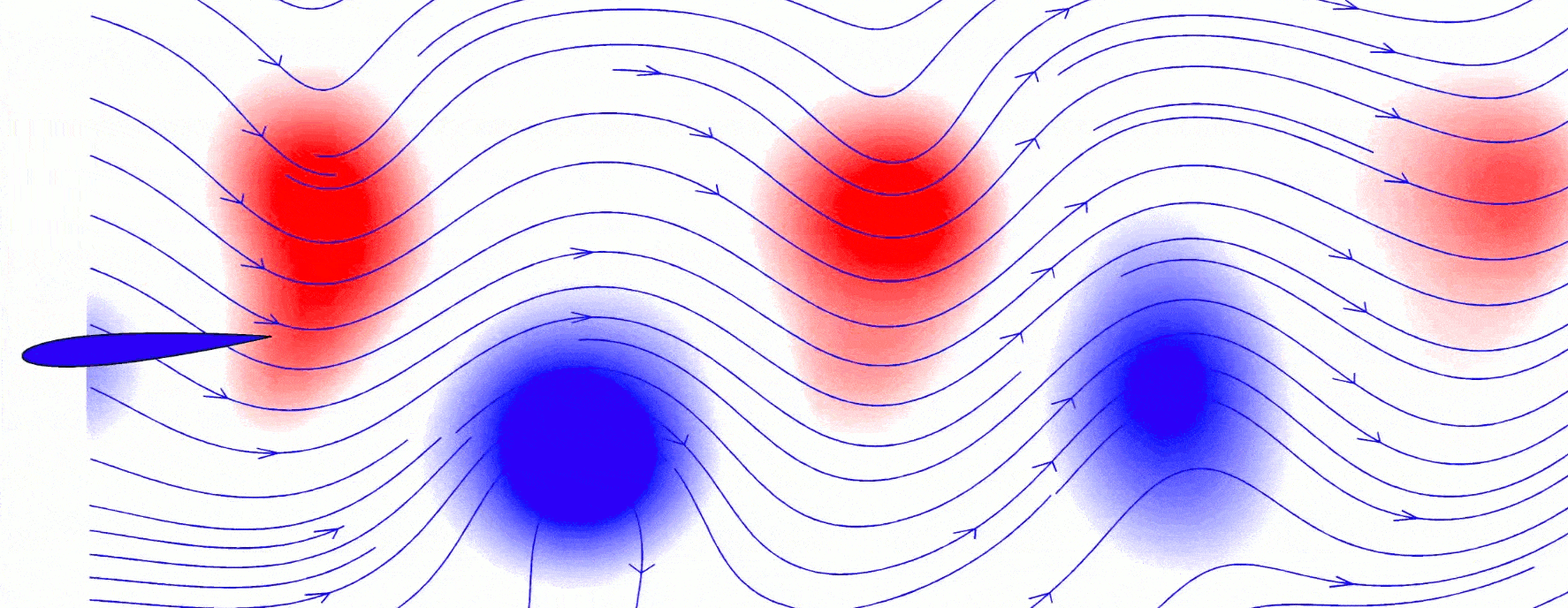
Sumario de ecuaciones y condiciones de contorno
Las ecuaciones que debe de verificar el campo de velocidad de perturbación son:
\( \nabla \cdot \vec{v}’ = 0\)
\( \nabla \times \vec{v}’ = 0 \)
Las condiciones de contorno que deben cumplir la solución propuesta son:
\(\|\vec{v}`\| \rightarrow 0 \ con \ \|\vec{x}\| \rightarrow \infty\)
\(v_{z}’ (x,0^{\pm},t) = \dfrac{\partial z_{e,i}}{\partial t} + U_{\infty} \dfrac{\partial z_{e,i}}{\partial x} \ con \ 0 \leq x \leq c\)
\(v_{z}’ (x,0^{-},t) = v_{z}’ (x,0^{+},t)\ con\ x \geq c\)
\(\dfrac{\partial \gamma (x,t)}{\partial t} + U_{\infty} \cdot \dfrac{\partial \gamma(x,t)}{\partial x} =0 \ con \ x \geq c\)
Resolución numérica: método de Vortex Lattice
Se propone como campo de velocidad de perturbación un campo continuo de torbellinos. Un torbellino centrado en la posición \(\vec{x}_{0}\) de circulación \(\Gamma(\vec{x}_{0})\) genera un campo de velocidades que viene del siguiente potencial:
\(\phi_{T} = – \dfrac{\Gamma(\vec{x}_{0})}{2 \pi} \cdot \tan^{-1} \left ( \dfrac{z-z_{0}}{x-x_{0}} \right )\)
Derivando dicho potencial con respecto a \(x\) y \(z\) se obtienen las velocidades de perturbación:
\(v’_{x,T} = \dfrac{\Gamma(\vec{x}_{0})}{2 \pi} \cdot \dfrac{z-z_{0}}{(x-x_{0})^{2} + (z-z_{0})^{2}} \)
\(v’_{z,T} = – \dfrac{\Gamma(\vec{x}_{0})}{2 \pi} \cdot \dfrac{x-x_{0}}{(x-x_{0})^{2} + (z-z_{0})^{2}} \)
Dicho campo de velocidades verifica directamente la ecuación de \( \nabla \times \vec{v}’ = 0 \) al venir de un potencial, y puede comprobarse que también cumple la otra ecuación de \( \nabla \cdot \vec{v}’ = 0\). Por otra parte verifica la condición de contorno en el infinito de que la velocidad perturbada tiende a 0.
Además, dicho campo de velocidades cumple las ecuaciones independientemente de dónde coloquemos los torbellinos y cuál sea su circulación. Por lo tanto, el campo de velocidades generado por un conjunto de torbellinos que suman su acción por principio de superposición también verifica las ecuaciones.
Si se asocia entonces a cada tramo infinitesimal \(dx_{0}\) del perfil y la estela un torbellino de circulación \(\gamma(x_{0},t) dx_{0}\), el campo de velocidades de perturbación creado por los torbellinos distribuidos en los puntos \((x_{0},z=0)\) viene dado por:
\(\displaystyle v’_{x}(x,z,t) = \dfrac{1}{2 \pi} \int_{0}^{c} \dfrac{z \cdot \gamma_{p}(x_{0},t) dx_{0}}{(x-x_{0})^{2} + z^{2}} + \dfrac{1}{2 \pi} \int_{c}^{\infty} \dfrac{z \cdot \gamma_{E}(x_{0},t) dx_{0}}{(x-x_{0})^{2} + z^{2}} \)
\(\displaystyle v’_{z}(x,z,t) = -\dfrac{1}{2 \pi} \int_{0}^{c} \dfrac{(x-x_{0}) \cdot \gamma_{p}(x_{0},t) dx_{0}}{(x-x_{0})^{2} + z^{2}} – \dfrac{1}{2 \pi} \int_{c}^{\infty} \dfrac{(x-x_{0}) \cdot \gamma_{E}(x_{0},t) dx_{0}}{(x-x_{0})^{2} + z^{2}} \)
Donde, para facilitar la distinción, se ha denominado como \(\gamma_{p}(x_{0},t)\) a los torbellinos presentes en el perfil y \(\gamma_{E}(x_{0},t)\) a los torbellinos presentes en la estela. Se observa que, en la estela, se verifica la continuidad de la velocidad vertical, es decir: \(v_{z}’ (x,0^{-},t) = v_{z}’ (x,0^{+},t)\).
Faltarían por lo tanto cumplir las condiciones de contorno del flujo en el perfil y la condición de que en la estela los torbellinos se propaguen con velocidad \(U_{\infty}\) manteniendo su intensidad. Particularizando el campo de velocidades para \(z=0\), es decir, en los puntos del perfil en los que la velocidad vertical es \(v_{z}’ (x,0,t) = w_{p} (x,t)\), las ecuaciones que quedan por cumplir son:
\(\displaystyle \boxed{w_{p} (x,t) = \dfrac{1}{2 \pi} \int_{0}^{c} \dfrac{\gamma_{p}(x_{0},t) dx_{0}}{x_{0} -x } + \dfrac{1}{2 \pi} \int_{c}^{\infty} \dfrac{\gamma_{E}(x_{0},t) dx_{0}}{x_{0} -x }} \ para \ 0 \leq x \leq c \)
\(\boxed{\dfrac{\partial \gamma_{E} (x,t)}{\partial t} + U_{\infty} \cdot \dfrac{\partial \gamma_{E}(x,t)}{\partial x} =0} \ para \ x \geq c\)
Supuesto conocido el movimiento del perfil \(w_{p} (x,t)\), la primera ecuación es una ecuación integral para los campos de torbellinos \(\gamma_{p}(x_{0},t)\) y \(\gamma_{E}(x_{0},t)\) que debe ser resuelta sujeta a la segunda ecuación que fuerza la evolución temporal y espacial que deben de seguir los torbellinos en la estela para validar la solución.
Además, faltaría una ecuación adicional para cerrar el problema, que permita poner un inicio al cálculo. Según el Teorema de Kelvin:
En un fluido barótropo ideal con fuerzas corporales conservadoras, la circulación alrededor de una curva cerrada (que encierra los mismos elementos del fluido) que se mueve con el fluido permanece constante con el tiempo. Es decir:
\(\dfrac{D \Gamma}{Dt} = 0\) Teorema de Kelvin (1869)
Inicialmente, con el perfil en reposo y con el flujo imperturbado, la circulación presente alrededor del perfil es nula:
\(\Gamma (x=c,t=0) = 0\)
Tras un intervalo de tiempo \(\Delta t \), el flujo ha recorrido una distancia \(U_{\infty} \cdot \Delta t \). Teniendo en cuenta el Teorema de Kelvin, la circulación debe cumplir:
\(\Gamma (x=c + U_{\infty} \cdot \Delta t ,t=\Delta t) = \Gamma (x=c,t=0) = 0\)

Teniendo por tanto la ecuación que cierra el problema:
\(\displaystyle \Gamma (x=c + U_{\infty} \cdot \Delta t ,t=\Delta t) = \boxed{\int_{0}^{c} \gamma_{p}(x_{0},t) dx_{0} + \int_{c}^{c + U_{\infty} \cdot \Delta t} \gamma_{E}(x_{0},t) dx_{0} = 0} \)
Ecuaciones integrales
Hemos definido el valor del campo vectorial de velocidades de perturbación \(\vec{v}'(x,z,t)\) en base a un campo escalar de torbellinos en el perfil \(\gamma_{p}(x,t)\) y en la estela \(\gamma_{E}(x,t)\). Nuestra preocupación ahora se resume a obtener el valor de dichos campos, y para ello debemos resolver las siguientes ecuaciones integrales:
\(\displaystyle w_{p} (x,t) = \dfrac{1}{2 \pi} \int_{0}^{c} \dfrac{\gamma_{p}(x_{0},t) dx_{0}}{x_{0} -x } + \dfrac{1}{2 \pi} \int_{c}^{c + U_{\infty} \cdot \Delta t} \dfrac{\gamma_{E}(x_{0},t) dx_{0}}{x_{0} -x } \ , \ 0 \leq x \leq c \)
\(\displaystyle\int_{0}^{c} \gamma_{p}(x_{0},t) dx_{0} + \int_{c}^{c + U_{\infty} \cdot \Delta t} \gamma_{E}(x_{0},t) dx_{0} = 0 \)
Con el campo de torbellinos en la estela sujeto a la siguiente ecuación diferencial:
\(\dfrac{\partial \gamma_{E} (x,t)}{\partial t} + U_{\infty} \cdot \dfrac{\partial \gamma_{E}(x,t)}{\partial x} =0 \ , \ x \geq c\)
Puesto que no es posible obtener una solución analítica para las ecuaciones integrales, el problema se resuelve numéricamente mediante el método de Vortex Lattice. En dicho método, se divide el perfil en \(N\) paneles, cada uno de longitud \(h=\dfrac{c}{N}\) provisto de un punto de centrado de torbellino, \(x_{gp_{j}} = h/4 + (j-1) \cdot h \ , \ con \ j=1 \dots N\), y de un punto de colocación \(x_{c_{j}} = h/2 + x_{gp_{j}} \ , \ con \ j=1 \dots N\), es decir a \(h/2\) del punto de centrado de torbellino.
El punto de centrado \(x_{gp_{j}}\) es la posición, para el panel \(j\), donde se encuentra situado el torbellino \(\gamma_{p_{j}}\), y el punto de colocación \(x_{c_{j}}\) es el punto de cada panel en el cuál se discretiza la integral. La posición de dichos puntos se debe a que numéricamente se ha comprobado que garantizan la solución más cercana a la real.
El problema se resuelve de manera cuasiestática, es decir, resolviendo las ecuaciones en un determinado instante \(t\) en el que los campos adquieren un cierto valor y dicha solución se emplea para calcular la correspondiente al instante \(t+\Delta t\).
El tiempo se discretiza en \(I\) instantes de duración \(\Delta t \), de forma que \(I = 1 \dots Nsteps\) tal que \( t = I \dot \Delta t\) siendo \(I \cdot \Delta t\) el instante final.
En el paso del instante \((I-1) \Delta t\) e \(I \Delta t\) se crea un nuevo torbellino en la estela, de longitud \(U_{\infty} \cdot \Delta t\) y densidad de circulación \(\gamma_{E_{I}}\) centrado en el punto llamado \(c^{+} = c + \dfrac{U_{\infty} \cdot \Delta t}{4}\) y se desplazan el resto de torbellinos ya existentes en la estela una distancia \(U_{\infty} \cdot \Delta t\) manteniendo su intensidad.
De esta forma, en el instante de tiempo \(I \Delta t\) las intensidades de los torbellinos en la estela son \(\gamma_{E_{I}}\) recién creado, y los \(\gamma_{E_{I-1}} \dots \gamma_{E_{2}} ,\gamma_{E_{1}}\) torbellinos creados en los instantes anteriores, cuyos puntos de centrado son \(x_{gE_{k}} = c + \dfrac{U_{\infty} \cdot \Delta t}{4} + (I – k) U_{\infty} \cdot \Delta t \ , \ con \ k=1 \dots I\). Así, automáticamente se cumple la ecuación diferencial sobre \(\gamma_{E}\) que limitaba la evolución de los torbellinos en la estela de forma que su derivada material es \(0\) puesto que se desplazan con la corriente manteniendo su intensidad constante.
Discretizando las ecuaciones integrales en cada uno de los paneles definidos sobre el perfil y los tramos en la estela asociados a cada torbellino, obtenemos las siguientes ecuaciones:
\(\displaystyle w_{p} (x_{c_{i}},t) = \sum_{j=1}^{N} \dfrac{h \cdot \gamma_{p_{j}}(t)}{2 \pi (x_{gp_{j}} – x_{c_{i}})} + \dfrac{U_{\infty} \Delta t \cdot \gamma_{E_{I}}}{2 \pi (c^{+} – x_{c_{i}})} + \sum_{k=1}^{I-1} \dfrac{U_{\infty} \Delta t \cdot \gamma_{E_{k}}}{2 \pi (x_{gE_{k}} – x_{c_{i}})}\)
Con \(i = 1 \dots N\), \(N\) ecuaciones para cada instante de tiempo.
\(\displaystyle 0 = \sum_{j=1}^{N} \gamma_{p_{j}}(t) + U_{\infty} \Delta t \cdot \gamma_{E_{I}} + \sum_{k=1}^{I-1} U_{\infty} \Delta t \cdot \gamma_{E_{k}}\)\(1\) ecuación para cada instante de tiempo.
Es decir, tenemos, en cada instante de tiempo \(t = I \Delta t\), \(N + 1\) ecuaciones para las \(N + 1\) incógnitas \(\gamma_{p_{1}}(t), \gamma_{p_{2}}(t) \dots \gamma_{p_{N-1}}(t) + \gamma_{p_{N}}(t)\) y \(\gamma_{E_{I}}(t)\).
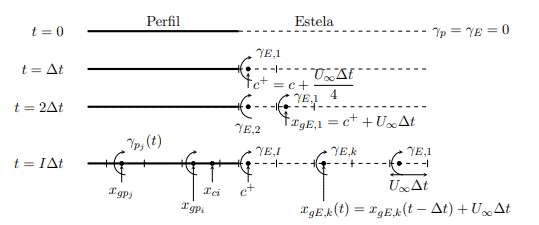
Por lo tanto, el sistema de ecuaciones puede resolverse matricialmente. Obsérvese que la separación en el sumatorio de los torbellinos correspondientes a instantes anteriores no se ha hecho por casualidad. Como dichos valores fueron obtenidos en instantes anteriores, no suponen incógnitas para el problema y ello permite la resolución.
Denominando a la velocidad vertical inducida en el perfil por los torbellinos previamente existentes en la estela \(k = 1 \dots I-1\) como wpEIm1:
wpEIm1(xc(i)) = \(\displaystyle \sum_{k=1}^{I-1} \dfrac{U_{\infty} \Delta t \cdot \gamma_{E_{k}}}{2 \pi (x_{gE_{k}} – x_{c_{i}})}\)
Y la contribución a la circulación debida a dichos torbellinos como GamEIm1:
GamEIm1(t) = \(\displaystyle \sum_{k=1}^{I-1} U_{\infty} \Delta t \cdot \gamma_{E_{k}}\)
El sistema de ecuaciones puede escribirse en forma matricial como:
\(\displaystyle \begin{bmatrix} A_{11} & \dots & \dots & \dots & A_{1N} & \dfrac{U_{\infty} \Delta t}{2 \pi (c^{+} – x_{c_{1}})} \\ \vdots & \ddots & & & \vdots & \vdots & \vdots \\ \vdots & & A_{ij} & & \vdots & \vdots \\ \vdots & & & \ddots & \vdots & \vdots\\ A_{N1} & \dots & \dots & \dots & A_{NN} & \dfrac{U_{\infty} \Delta t}{2 \pi (c^{+} – x_{c_{N}})} \\ h & \dots & \dots & \dots & h & U_{\infty} \Delta t\end{bmatrix} \cdot \begin{bmatrix} \gamma_{p1} \\ \gamma_{p2} \\ \vdots \\ \vdots \\ \gamma_{pN} \\ \gamma_{E_{I}} \end{bmatrix} = \begin{bmatrix} w_{p1}(t) – wpEIm1(xc(1)) \\ \vdots \\ \vdots \\ \vdots \\ w_{pN}(t) – wpEIm1(xc(N)) \\ -GamEIm1(t) \end{bmatrix}\)Donde se han definido:
\(A_{ij} = \dfrac{h}{2 \pi (x_{gp_{j}} – x_{c_{i}})}\)
y
\( \ \ \ \ \ w_{pi}(t) = w_{p}(x_{c_{i}},t)\)
En forma compacta el sistema matricial puede expresarse como \(B \cdot \vec{\gamma} = \vec{r}\), siendo por lo tanto posible obtener la solución de las densidades de circulación en el perfil \(\gamma_{p_{1}}(t), \gamma_{p_{2}}(t) \dots \gamma_{p_{N-1}}(t) + \gamma_{p_{N}}(t)\) y la del torbellino recién creado en la estela \(\gamma_{E_{I}}(t)\) en el instante \(t=I \Delta t\) realizando \(\vec{\gamma} = B^{-1} \cdot \vec{r}\).
Con la densidad de circulación en el perfil en el instante considerado es posible calcular la sustentación t el momento de cabeceo en dicho instante respecto a un punto cualquiera \(x_{a}\) del perfil.
Recordemos que la presión perturbada viene dada por:
\( p'(x,z,t) = -\rho_{\infty} \dfrac{\partial \phi (x,z,t)}{\partial t } – \rho_{\infty} U_{\infty} v_{x}'(x,z,t)\)
Y la diferencia de presiones entre extradós e intradós viene dada por:
\( \Delta p = (p_{\infty} + p'(x,0^{-},t)) – (p_{\infty} + p'(x,0^{+},t)) = \)
\( = \rho_{\infty} \dfrac{\partial }{\partial t } \left \{ \phi (x,0^{+},t) – \phi (x,0^{-},t) \right \} – \rho_{\infty} U_{\infty} \left \{v_{x}'(x,0^{+},t) – v_{x}'(x,0^{-},t) \right \}\)
Como sabemos que:
\( \displaystyle \phi(x,0^{+},t) – \phi(x,0^{-},t) = \Gamma(x,t) = \int_{0}^{x} \gamma (x,t) dx_{0}\)
\(v(x,0^{+},t) – v(x,0^{-},t) = \gamma(x,t) \)
Podemos expresar la diferencia de presiones en un punto del perfil como:
\( \Delta p = \rho_{\infty} \dfrac{\partial \Gamma_{p} (x,t)}{\partial t} + \rho_{\infty} U_{\infty} \gamma_{p}(x,t) \)
Nótese que se ha puesto el índice \(p\) para especificar que sólo se cumple en el perfil; en la estela dicha diferencia de presión es nula como hemos visto anteriormente.
Como hemos discretizado los torbellinos en cada panel, debemos discretizar también la diferencia de presión en cada panel \(j\) tal que tenemos una \( \Delta p (x_{j},t) \) constante en cada panel. La circulación hasta el panel \(j\) viene dada por:
\(\displaystyle \Gamma_{p_{j}}(t) = \sum_{l=1}^{j} \gamma_{p_{l}} \cdot h\)
Finalmente la diferencia de presión en cada panel viene dada por:
\(\Delta p (x_{j},t) = \rho_{\infty} \dfrac{\Gamma_{p_{j}} (t) – \Gamma_{p_{j}} (t-\Delta t) }{\Delta t} + \rho_{\infty} U_{\infty} \gamma_{p_{j}}(t)\)
Y la sustentación por unidad de envergadura en el instante \(t = I \Delta t\) es:
\(\displaystyle L(t) = \int_{0}^{c} \Delta p (x,t) dx = \sum_{j=1}^{N} \Delta p_{j}(t) \cdot h\)
En cada panel se aplica una fuerza por unidad de envergadura de valor \(\Delta p_{j}(t) \cdot h\) en el punto medio del panel definido como \(x_{m_{j}} = \dfrac{x_{gp_{j}} + x_{c_{j}}}{2}\). Por lo tanto, el momento de cabeceo por unidad de envergadura con respecto a un punto genérico \(x_{A}\) se define como:
\(\displaystyle M_{A}(t) = \int_{0}^{c} (x_{A} – x) \cdot \Delta p (x,t) dx = \sum_{j=1}^{N} (x_{A} – x_{m_{j}}) \cdot \Delta p_{j}(t) \cdot h\)
Donde dicho momento (cabeceo) se ha definido con signo positivo en sentido horario como suele hacerse en aerodinámica.
A continuación se adjunta un código de MATLAB para ejecutar dicho método:
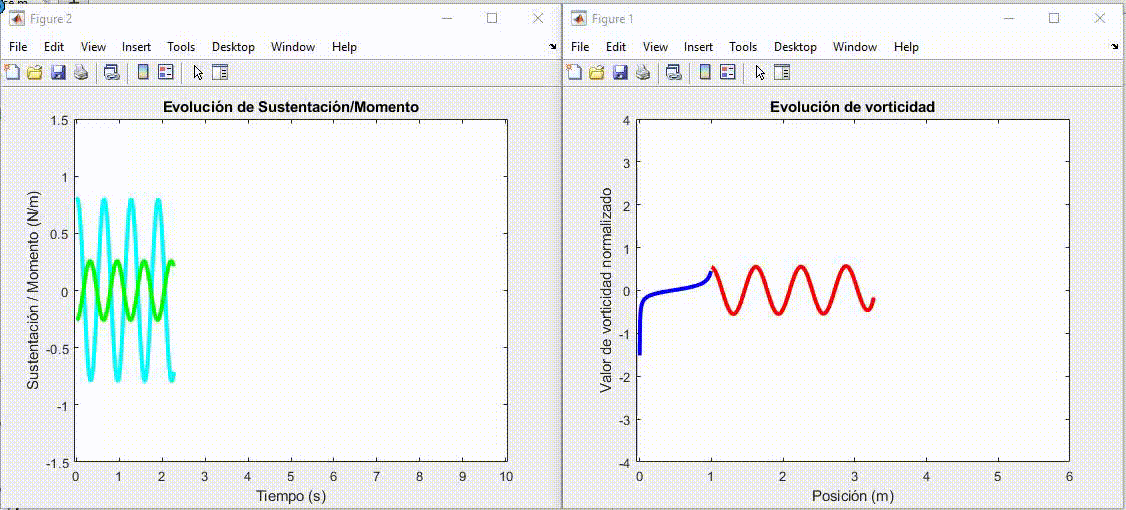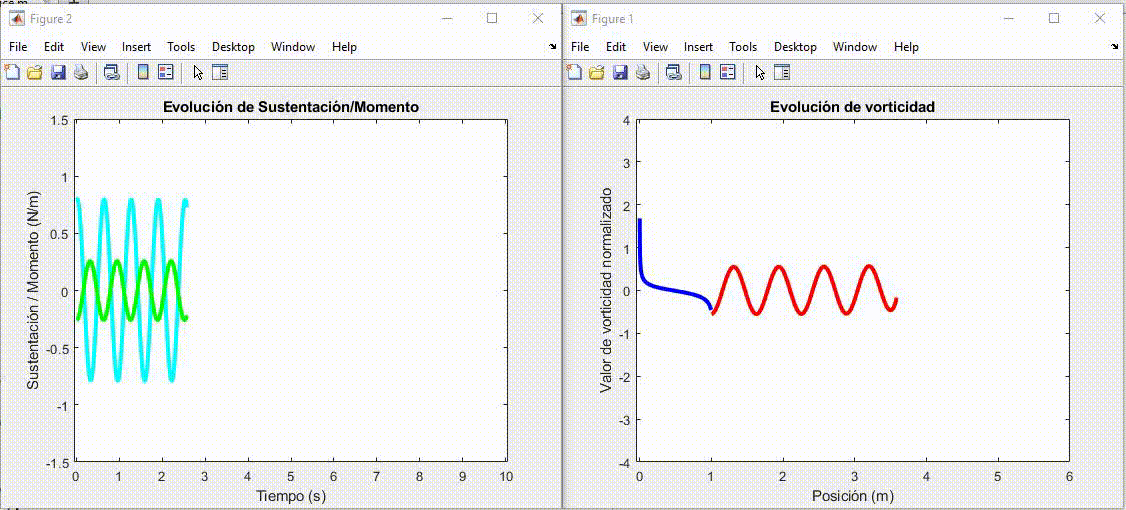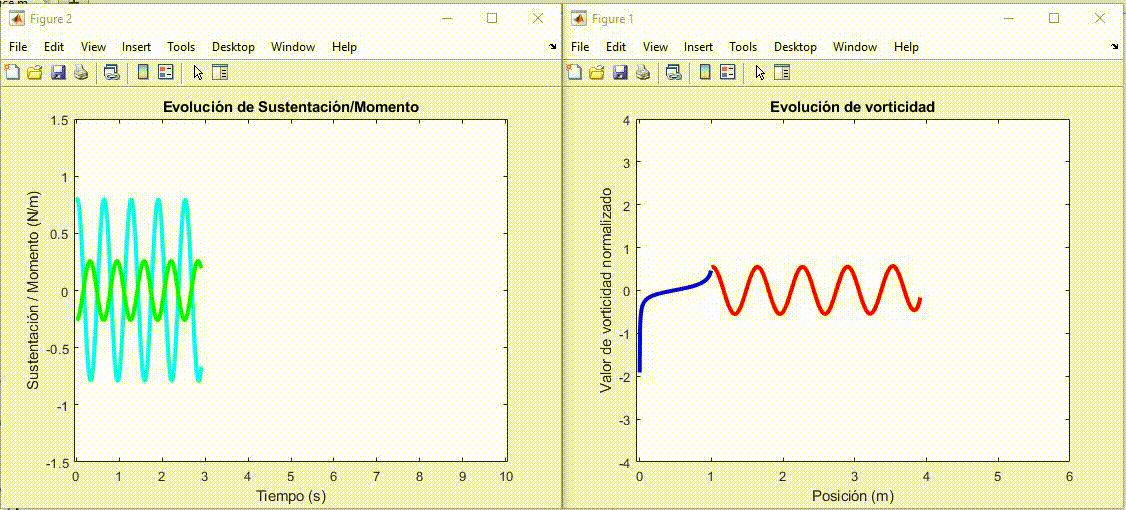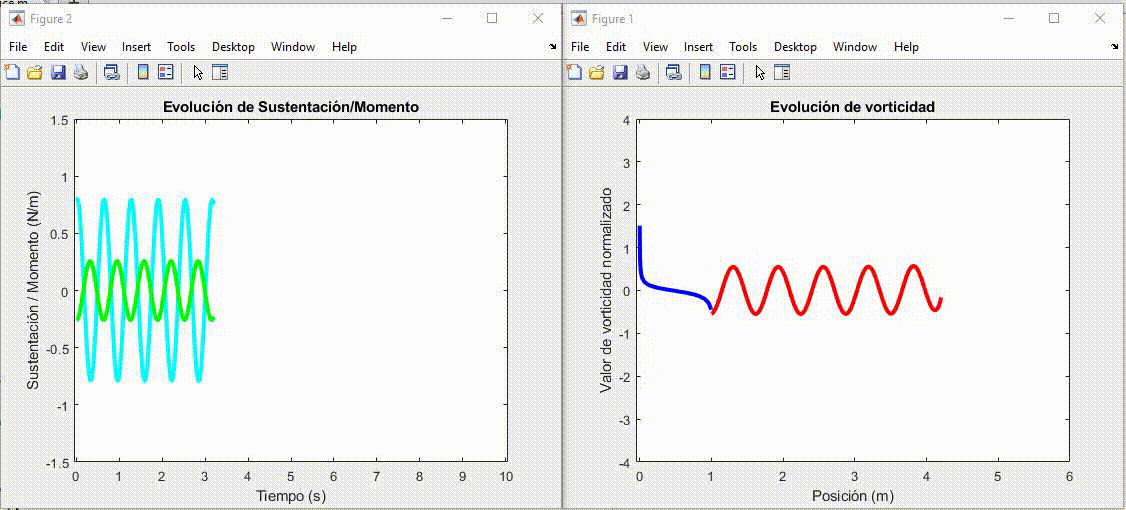
Azul: Valor normalizado de vorticidad en perfil
Roja: Valor normalizado de vorticidad en estela
Cyan: Sustentación
Verde: Momento en A
clc
clear all
close all
% Parametros de vuelo:
Uinf=1;
rhoinf=1;
c=1;
% Panelado
N=200;
h=c/N;
% Tiempo
t_total=10;
Nsteps=1000;
dt=t_total/Nsteps;
% Puntos de los torbellinos
xgp(1:N)=h/4+((1:N)-1)*h;
% Puntos de colocacion
xc(1:N)=xgp+h/2;
% Puntos medios
xm(1:N)=(xc+xgp)/2;
% Matriz Aij
for i=1:N
for j=1:N
A(i,j)=(h/(2*pi))*(1/(xgp(j)-xc(i)));
end
end
% Matriz B
b=c/2;
cmas=c+Uinf*dt/4;
B(1:N,1:N)=A;
B(1:N,N+1)=(Uinf*dt/(2*pi)).*(1./(cmas-xc(1:N)));
B(N+1,1:N)=h;
B(N+1,N+1)=Uinf*dt;
%Binv=inv(B);
% Avance en el tiempo
GampxIm1(1:N)=0;
for I=1:Nsteps
t=I*dt;
tv(I)=t;
if I>1
xgE(1:I-1)=Uinf*dt+xgE(1:I-1);
GamEIm1=Uinf*dt*sum(gamE(1:I-1));
for i=1:N
wpEIm1(i)=(Uinf*dt/(2*pi))*sum(gamE(1:I-1)./(xgE(1:I-1)-xc(i)));
end
else % Para el primer instante..
GamEIm1=0;
wpEIm1(1:N)=0;
fprintf('Azul: Valor normalizado de vorticidad en perfil \n Roja: Valor normalizado de vorticidad en estela \n')
fprintf('Cyan: Sustentación \n Verde: Momento en A \n')
end
% Movimiento oscilatorio del perfil
dzpdx=0;
h0=0.01*c;
omega=5*Uinf/b;
zp(1:N)=h0*cos(omega*t);
dzpdt=-h0*omega*sin(omega*t);
wp=dzpdt+Uinf*dzpdx;
% Solucion de densidad de circulacion
gamsol=B\[wp-wpEIm1,-GamEIm1]';
% Densidad de circulacion sobre el perfil
gamp(1:N)=gamsol(1:N);
gamE(I)=gamsol(N+1);
xgE(I)=cmas;
figure(1)
plot(xgp,gamp/Uinf,'b','LineWidth',3);
title('Evolución de vorticidad')
hold on
plot(xgE(1:I), gamE(1:I)/Uinf,'r','LineWidth',3)
%legend('Magnitud normalizada de torbellinos en perfil','Magnitud normalizada de torbellinos en estela')
axis([-0.05 c+5*c -4 4])
xlabel('Posición (m)')
ylabel('Valor de vorticidad normalizado')
hold off
% Circulacion a t hasta el punto j
Gampx(1)=gamp(1)*h;
for i=2:N
Gampx(i)=Gampx(i-1)+gamp(i)*h;
end
% Diferencia de presion intrados extrados
pimpe=rhoinf*((Gampx(1:N)-GampxIm1(1:N))/dt)+rhoinf*Uinf*gamp(1:N);
% Sustentacion
L(I)=sum(pimpe*h);
% Momento
xA=b/3;
MA(I)=sum(pimpe*h.*(xA-xm));
% Actualizacion de la circulacion al instante I-1
GampxIm1=Gampx;
figure(2)
plot(tv,L,'c','LineWidth',3);
hold on
plot(tv,MA,'g','LineWidth',3);
title('Evolución de Sustentación/Momento')
xlabel('Tiempo (s)')
ylabel('Sustentación / Momento (N/m)')
axis([-0.05 10.05 -1.5 1.5])
hold off
endAcoplamiento con movimiento general
En el punto anterior hemos supuesto un movimiento del perfil y en base a ello hemos obtenido la evolución del flujo. Sin embargo, en la realidad el movimiento del perfil no es dado sino que depende precisamente del flujo. Para ver la evolución de un perfil en el flujo podemos acoplar la dinámica del perfil con la aerodinámica no estacionaria que acabamos de ver.
Vamos a considerar un perfil de cuerda \(c\), masa \(m\), inercia en el centro de masas \(I_{G}\) y posición del centro de masas a una distancia \(x_{G}\) del borde de ataque.
La placa posee a una distancia \(x_{e}\) (posición eje elástico) un muelle de constante elástica \(K_{h}\) y un muelle a torsión de constante \(K_{\alpha}\).
Consideraremos como grados de libertad el desplazamiento vertical del eje elástico en \(e\), \(h_{e}\) (positivo hacia abajo) y el ángulo girado alrededor de dicho punto \(\alpha(t)\) que coincide con el ángulo que forma la placa con la corriente.
El esquema de fuerzas y grados de libertad sería el siguiente considerando el principio de d’Alembert:
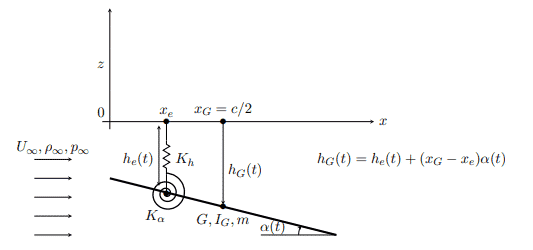
Las ecuaciones dinámicas resultantes son las siguientes:
\(L(t) + K_{h} \cdot h_{e} (t)+ m \cdot \ddot h_{G} (t)= 0\)
\(I_{G} \cdot \ddot \alpha (t)+ K_{\alpha} \cdot \alpha (t) – M_{G} (t) – K_{h} \cdot h_{e} (t) \cdot (x_{G} – x_{e}) = 0\)
Si expresamos \(\ddot h_{G}\) en función de los grados de libertad obtenemos:
\(\ddot h_{G} (t) = \ddot h_{e} (t) + \ddot \alpha (t) \cdot (x_{G} – x_{e})\)
Y despejando los grados de libertad de las ecuaciones obtenemos:
\(\boxed{\ddot h_{e} (t) = \dfrac{-L(t) – K_{h} \cdot h_{e} (t) – m \cdot \ddot \alpha (t) \cdot (x_{G} – x_{e})}{m}}\)
\(\boxed{\ddot \alpha (t)= \dfrac{M_{G} (t) + K_{h} \cdot h_{e} (t) \cdot (x_{G} – x_{e}) – K_{\alpha} \cdot \alpha (t)}{I_{G}}} \)
Es decir, dos ecuaciones diferenciales de segundo orden y por lo tanto necesitaremos especificar las condiciones iniciales \(h_{e} (0), \dot h_{e} (0), \alpha (0), \dot \alpha (0)\).
Para poder acoplar el método de Vortex-Lattice con la dinámica del perfil seguimos el siguiente esquema:
- Las condiciones iniciales \(\dot h_{e} (0), \dot \alpha (0)\) nos proporcionan una velocidad inicial del perfil \(w_{p}(0)\).
- Obtenemos el valor de la sustentación y el momento en dicho instante inicial \(L(0), M_{G}(0)\).
- Con las condiciones iniciales en posición \( h_{e} (0), \alpha (0)\) calculamos las fuerzas elásticas.
- Podemos obtener el valor de \(\ddot h_{e} (0), \ddot \alpha (0)\) de las ecuaciones anteriores.
Una vez tenemos el valor de las derivadas segundas podemos obtener de manera lineal el valor de las condiciones iniciales del instante posterior (en el instante inicial \(I = 0\)):
\(\dot h_{e} (I+1) = \dot h_{e}(I) + \Delta t \cdot \ddot h_{e} (I) \\\) \(h_{e} (I+1) = h_{e} (I) + \Delta t \cdot \dot h_{e}(I) \\\) \(\dot \alpha (I+1) = \dot \alpha (I) + \Delta t \cdot \ddot \alpha (I) \\\) \(\alpha (I+1) = \alpha (I) + \Delta t \cdot \dot \alpha (I) \\ \)El procedimiento entonces se repite hasta completar el intervalo de tiempo a estudiar. A continuación se adjunta un código de MATLAB para ejecutar dicho método (al inicio se produce una gran sustentación y vorticidad en la estela; se debe al torbellino de arranque al partir del reposo):
Azul: Valor normalizado de vorticidad en perfil
Roja: Valor normalizado de vorticidad en estela
Cyan: Sustentación
Verde: Momento en A
clc
clear all
close all
% Parametros:
Uinf=1;
rhoinf=1;
c=1;
%PLACA:
m=0.8*1.5708;
Kh = 10*0.5674;
Kalpha=10*0.15;
xe = 0.3*c;
xG = 0.5*c;
IG = 0.8*0.0355;
% Panelado
N=200;
h=c/N;
% Tiempo
t_total=8;
Nsteps=1000;
dt=t_total/Nsteps;
% Valores iniciales
he0=-c/10;
dhe0=0;
alpha0=pi/32;
dalpha0=0;
% Puntos de los torbellinos
xgp(1:N)=h/4+((1:N)-1)*h;
% Puntos de colocacion
xc(1:N)=xgp+h/2;
% Puntos medios
xm(1:N)=(xc+xgp)/2;
% Matriz Aij
for i=1:N
for j=1:N
A(i,j)=(h/(2*pi))*(1/(xgp(j)-xc(i)));
end
end
% Matriz B
b=c/2;
cmas=c+Uinf*dt/4;
B(1:N,1:N)=A;
B(1:N,N+1)=(Uinf*dt/(2*pi)).*(1./(cmas-xc(1:N)));
B(N+1,1:N)=h;
B(N+1,N+1)=Uinf*dt;
%Binv=inv(B);
% Avance en el tiempo
GampxIm1(1:N)=0;
for I=1:Nsteps
t=I*dt;
tv(I)=t;
if I>1
he(I)=he(I-1)+dhe(I-1)*dt;
dhe(I)=dhe(I-1)+d2he(I-1)*dt;
alpha(I)=alpha(I-1)+dalpha(I-1)*dt;
dalpha(I)=dalpha(I-1)+d2alpha(I-1)*dt;
xgE(1:I-1)=Uinf*dt+xgE(1:I-1);
GamEIm1=Uinf*dt*sum(gamE(1:I-1));
for i=1:N
wpEIm1(i)=(Uinf*dt/(2*pi))*sum(gamE(1:I-1)./(xgE(1:I-1)-xc(i)));
end
else % Para el primer instante..
he(I)=he0;
dhe(I)=dhe0;
alpha(I)=alpha0;
dalpha(I)=dalpha0;
GamEIm1=0;
wpEIm1(1:N)=0;
fprintf('Azul: Valor normalizado de vorticidad en perfil \n Roja: Valor normalizado de vorticidad en estela \n')
fprintf('Cyan: Sustentación \n Verde: Momento en A \n')
end
% Movimiento del perfil
wp(1:N)=-Uinf*(alpha(I)+dhe(I)/Uinf)-(xc(1:N)-xe)*dalpha(I);
% Solucion de densidad de circulacion
gamsol=B\[wp-wpEIm1,-GamEIm1]';
% Densidad de circulacion sobre el perfil
gamp(1:N)=gamsol(1:N);
gamE(I)=gamsol(N+1);
xgE(I)=cmas;
figure(1)
plot(xgp,gamp/Uinf,'b','LineWidth',3);
title('Evolución de vorticidad')
hold on
plot(xgE(1:I), gamE(1:I)/Uinf,'r','LineWidth',3)
%legend('Magnitud normalizada de torbellinos en perfil','Magnitud normalizada de torbellinos en estela')
axis([-0.05 c+5*c -4 4])
xlabel('Posición (m)')
ylabel('Valor de vorticidad normalizado')
hold off
% Circulacion a t hasta el punto j
Gampx(1)=gamp(1)*h;
for i=2:N
Gampx(i)=Gampx(i-1)+gamp(i)*h;
end
% Diferencia de presion intrados extrados
pimpe=rhoinf*((Gampx(1:N)-GampxIm1(1:N))/dt)+rhoinf*Uinf*gamp(1:N);
% Sustentacion
L(I)=sum(pimpe*h);
% Momento
xG=c/2;
MG(I)=sum(pimpe*h.*(xG-xm));
% Actualizacion de la circulacion al instante I-1
GampxIm1=Gampx;
figure(2)
plot(tv,L,'c','LineWidth',3);
hold on
plot(tv,MG,'g','LineWidth',3);
title('Evolución de Sustentación/Momento')
xlabel('Tiempo (s)')
ylabel('Sustentación / Momento (N/m)')
axis([-0.05 8.05 -1.5 1.5])
hold off
d2alpha(I)=(MG(I)+Kh*he(I)*(xG-xe)-Kalpha*alpha(I))/IG;
d2he(I)=(-L(I)-Kh*he(I)-m*d2alpha(I)*(xG-xe))/m;
end



