Las ecuaciones de Lagrange son un conjunto de ecuaciones que nos permiten conocer la ecuación diferencial del movimiento de las coordenadas libres que estemos estudiando. Tendremos un número de ecuaciones igual al número de grados de libertad.
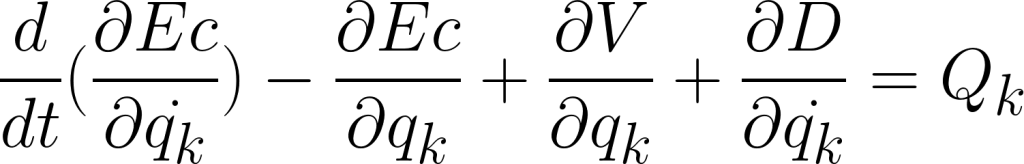
La mecánica analítica
La mecánica analítica es una formulación abstracta y general de la mecánica clásica, siendo la principal alternativa a la mecánica newtoniana o vectorial.
A diferencia de la mecánica newtoniana, sólo válida para sistemas de referencia no inerciales, en la que se emplean sistemas de referencia, vectores, vínculos cinemáticos, etc… La mecánica analítica se centra en la parte puramente matemática de la física, deduciendo expresiones a partir de formas escalares (Energía, potencias), de manera que no aparecen vectores, reacciones o movimiento relativo. Además de ser válida para sistemas de referencia inerciales.
Es decir, que podemos resolver el movimiento de un mecanismo sin ni siquiera saber o imaginar cómo dicho mecanismo se moverá o cuál es el valor de las reacciones vinculares. Esta ventaja hace esencial el uso de la mecánica analítica para resolver problemas en varias variables o mecanismos más complejos.

Deducción de las ecuaciones de Lagrange
Para llegar a la forma final de las ecuaciones de Lagrange deberemos de pasar por el Principio de D’Alembert, el Principio de los trabajos virtuales y, tras la introducción de las coordenadas generalizadas llegaremos a las ecuaciones finales.
Principio D’Alembert
Cuando estudiamos un problema en estática, estudiamos un problema que no se mueve. Partiendo de condiciones iniciales de velocidad nula, la forma de evitar que dicha estructura o cuerpo se mueva sería haciendo nula cualquier aceleración.
De la 2ª Ley de Newton se tiene que
\(\sum_{i=1}^{n} \vec{F_{i}}= m*\vec{a}\)La cual en estática verifica que \(\sum_{i=1}^{n} \vec{F_{i}}=\vec{0}\)
Que es la ecuación fundamental de la estática para calcular las reacciones que evitan que por ejemplo los cuerpos atraviesen el suelo o hagan movimientos imposibles.
En el caso de la dinámica se estudia cómo un sistema se mueve bajo la acción de fuerzas. Esto hace que nuestra ecuación sea:
\(\sum_{i=1}^{n} \vec{F_{i}}= m*\vec{a}\)Y que, conociendo el valor de las fuerzas, nos permite conocer la aceleración que, tras integrar y aplicar condiciones iniciales, nos da la trayectoria.
El Principio de D’Alembert es muy sencillo, y consiste en definir una fuerza de inercia tal que en todo momento sea igual a la masa por la aceleración con signo opuesto. Es decir;
\(\vec{F_{in}}=-m\vec{a}\)De esta forma, podemos estudiar un problema de dinámica aplicando todas las propiedades y principios de la estática añadiendo esta fuerza de inercia a nuestra fórmula;
\(\sum_{i=1}^{n} \vec{F_{i}} + \vec{F_{in}} = \vec{0} \)
Fuerzas de inercia en sólido rígido
En el caso de tener un problema en el que la masa se encuentre concentrada en un punto sin dimensiones es evidente que
\(\vec{F_{in}}=-m*\vec{a}\) , siendo \(\vec{a}\) la aceleración de dicha partícula y m su masa.
Sin embargo, si tenemos un sólido rígido no es tan fácil computar la fuerza de inercia de todo el cuerpo.En nuestro caso tendríamos:
\(\vec{F_{in}}= \int d \vec{F_{in}} = \int_{V} \vec{a} \ dm = \int_{V} (\rho \vec{a}) \ dV\)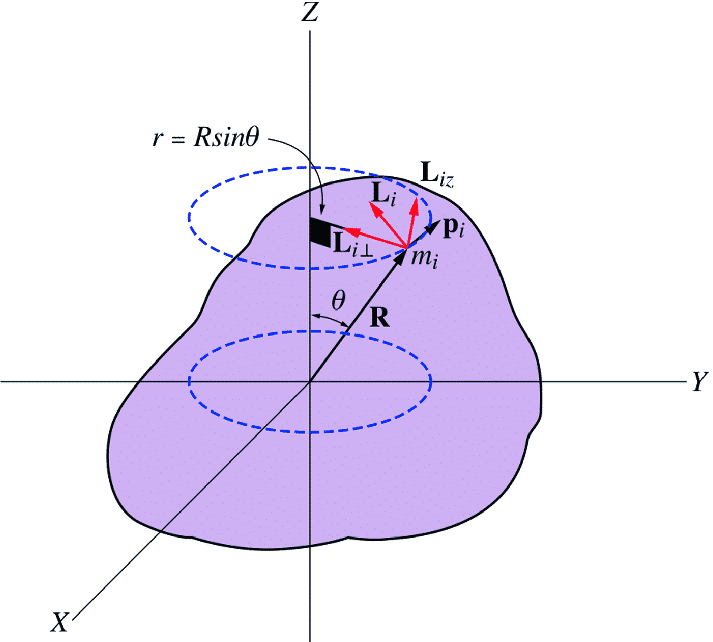
Cuya distribución variará en función de la forma y tamaño del cuerpo.
Sin embargo, podemos establecer de forma general que el movimiento del cuerpo vendrá definido por una fuerza de inercia igual a la masa total * la aceleración del centro de gravedad + un momento angular aplicado en el centro de gravedad definido por la aceleración angular y el momento de inercia baricéntrico.
Aquí puedes ver los momentos de inercia baricéntricos de figuras conocidas
\(\vec{F}_{in}= -m\vec{a_{G}}\)
\(\vec{M} _{in} = -J_{G} \vec{\ddot{\theta}}\)
Principio de los Trabajos Virtuales
Podemos generalizar el Principio de los Trabajos Virtuales para el caso de la dinámica aplicando el Principio de D’Alembert.
El Principio de los Trabajos Virtuales establece que un sistema está en equilibrio cuando el trabajo virtual total de las fuerzas actuantes, sin contar las vinculares, sobre sus cuerpos es cero.
Se elimina la acción de la fuerzas vinculares porque en el caso de los vínculos lisos (99% de los problemas teóricos de ingeniería) estos ejercen una fuerza perpendicular al movimiento, de manera que no realizan trabajo.
El trabajo virtual de una fuerza es:
\(\delta W_{i} = F_{i}*\delta \vec{r_{i}}\)
El trabajo virtual total es:
\(\delta W = \sum_{i=1}^{n} F_{i}*\delta \vec{r_{i}}=0\)
Introduciendo el Principio de D’Alembert y generalizando para un sistema de nc cuerpos y nf fuerzas:
\(\delta \mathcal{L} =\sum_{i=1}^{nc} \sum_{j=1}^{nf} (\vec{F_{ij}}*\delta \vec{P_{ij}})+ \sum_{i=1}^{nc} (-m_{i}*\vec{a_{G_{i}}}*\delta \vec{G_{i}}- J_{G_{i}}*\vec{\ddot {\theta_{i}}}*\delta \vec{\theta _{i} } ) =0\)Que, desarrollando los términos de desplazamiento de la posición y el centro de gravedad:
\(\delta \mathcal{L} = \sum_{i=1}^{nc} \sum_{j=1}^{nf} (F_{x_{ij}} \cdot \delta x_{ij} + F_{y_{ij}} \cdot \delta y_{ij}) + \\\) \( + \sum_{i=1}^{nc} (-m_{i}*a_{G_{xi}}*\delta x_{Gi}- m_{i}*a_{G_{yi}}*\delta y_{Gi} – J_{G_{i}}*\ddot {\theta_{i}}*\delta \theta_{i} ) =0\)Sin embargo observamos que aparecen muchos términos con \(\delta\) los cuales no podemos calcular. Vamos a expresar todos esos términos en función de un \(\delta\) común, el de las coordenadas generalizadas.
Siendo \(q_{1},q_{2}…q_{n}\) nuestros grados de libertad (Posición x, rotación…) hacemos el siguiente cambio:
\(\delta x = \sum_{k=1}^{n}( \frac{\partial x}{\partial q_{k}} * \delta q_{k})\) \(\delta y = \sum_{k=1}^{n}( \frac{\partial y}{\partial q_{k}} * \delta q_{k})\) \(\delta \theta = \sum_{k=1}^{n}( \frac{\partial \theta}{\partial q_{k}} * \delta q_{k})\)Y definiendo las componentes Lagrangianas como
\(Q_{k} = \sum_{i=1}^{nc} \sum_{j=1}^{nf} (F_{x_{ij}} \cdot \frac{\partial x_{ij}}{\partial q_{k}} + F_{y_{ij}} \cdot \frac{\partial y_{ij}}{\partial q_{k}}) \\\) \(Q_{in,k}= \sum_{i=1}^{nc} (-m_{i}*a_{G_{xi}}* \frac{\partial x_{Gi}}{\partial q_{k}} – m_{i}*a_{G_{yi}}* \frac{\partial y_{Gi}}{\partial q_{k}} – J_{G_{i}}*\ddot {\theta_{i}}* \frac{\partial \theta_{i}}{\partial q_{k}} ) \)Podemos expresar el trabajo virtual de esta forma:
\(\delta \mathcal{L} =\sum_{k=1}^{n} ( Q_{k} + Q_{in,k} )*\delta q_{k}=0\)De lo cual extraemos que, al ser \(q_{k}\) cada uno de nuestros grados de libertad, al existir movimiento \(\delta q_{k} \not = 0\) , lo cual nos conduce al siguiente sistema de ecuaciones:
Q_{1}+Q_{in,1}=0
Q_{2}+Q_{in,2}=0
…
Q_{n}+Q_{in,n}=0
Existiendo una ecuación para cada grado de libertad \(q_{k}\)
Estas serían las ecuaciones de Lagrange en su forma más primitiva. La gracia de usar estas ecuaciones es usar unas ecuaciones intuitivas en las que podamos identificar cada término, y es el desarrollo que realizaremos a continuación.
Energía cinética
Vamos a empezar desarrollando el término \(Q_{in}\), correspondiente a las fuerzas de inercia.
\(Q_{in,k}= \sum_{i=1}^{nc} (-m_{i}*a_{G_{xi}}* \frac{\partial x_{Gi}}{\partial q_{k}} – m_{i}*a_{G_{yi}}* \frac{\partial y_{Gi}}{\partial q_{k}} – J_{G_{i}}*\ddot {\theta_{i}}* \frac{\partial \theta_{i}}{\partial q_{k}} ) \) \(= \sum_{i=1}^{nc} ( -m_{i}*\vec{a_{G_{i}}}*\frac{\partial \vec{G_{i}}}{\partial q_{k}}- J_{G_{i}}*\vec{\ddot {\theta_{i}}}*\frac{\partial \vec{\theta _{i} }}{\partial q_{k}} )\) \(= \sum_{i=1}^{nc} ( -m_{i}* \frac{d\vec{v_{G_{i}}}}{dt}*\frac{\partial \vec{G_{i}}}{\partial q_{k}}- J_{G_{i}}* \frac{d\vec{\dot {\theta_{i}}}}{dt} *\frac{\partial \vec{\theta _{i} }}{\partial q_{k}} )\) \(= \sum_{i=1}^{nc} ( -m_{i}* [\frac{d}{dt}( \vec{v_{G_{i}}} *\frac{ \partial \vec{G_{i}}}{\partial q_{k}})- \vec{v_{G_{i}}} * \frac{d}{dt} ( \frac{\partial \vec{G_{i}}}{\partial q_{k}} )] – J_{G_{i}}* [\frac{d}{dt}( \vec{ \dot {\theta_{i}} } *\frac{ \partial \vec{ \theta _{i}}}{\partial q_{k}})- \vec{ \dot {\theta_{i}} } * \frac{d}{dt} ( \frac{\partial \vec{ \theta _{i} }}{\partial q_{k}} )] )\)En este punto hacemos una pausa y consideramos los siguientes cambios:
\( \vec{v}=\frac{d\vec{r}}{t}= \frac{ \partial \vec{r}}{ \partial q } * \frac{ dq }{dt} = \frac{ \partial \vec{r}}{ \partial q } * \dot{q} \rightarrow \rightarrow \frac{ \partial \vec{r}}{ \partial q } = \frac{ \partial \vec{v}}{ \partial \dot{q} } \)
\( \vec{ \dot{\theta} }=\frac{d\vec{\theta}}{t}= \frac{ \partial \vec{ \theta }}{ \partial q } * \frac{ dq }{dt} = \frac{ \partial \vec{ \theta }}{ \partial q } * \dot{q} \rightarrow \rightarrow \frac{ \partial \vec{ \theta }}{ \partial q } = \frac{ \partial \vec{ \dot{\theta} }}{ \partial \dot{q} } \)
\( \frac{d}{dt} ( \frac{\partial \vec{ r}}{\partial q}) = \frac{\partial \vec{ v}}{\partial q} \)
\( \frac{d}{dt} ( \frac{\partial \vec{ \theta }}{\partial q}) = \frac{\partial \vec{ \dot{\theta }}}{\partial q} \)
\(= \sum_{i=1}^{nc} ( -m_{i}* [\frac{d}{dt}( \vec{v_{G_{i}}} *\frac{ \partial \vec{v_{G_{i}}} }{\partial \dot{q_{k}}})- \vec{v_{G_{i}}} * \frac{\partial \vec{v_{G_{i}}} }{\partial q_{k}} ] – J_{G_{i}}* [\frac{d}{dt}( \vec{ \dot {\theta_{i}} } * \frac{ \partial \vec{ \dot{\theta_{i}} }}{ \partial \dot{q_{k}} } )- \vec{ \dot {\theta_{i}} } * \frac{\partial \vec{\dot{ \theta _{i} }}}{\partial q_{k}} ] )\) \(= \sum_{i=1}^{nc} ( -m_{i}* [\frac{d}{dt}( \frac{ \partial \frac{1}{2} \vec{v_{G_{i}}}^{2} }{\partial \dot{q_{k}}})- \frac{\partial \frac{1}{2} \vec{v_{G_{i}}}^{2} }{\partial q_{k}} ] – J_{G_{i}}* [\frac{d}{dt}( \frac{ \partial \frac{1}{2} \vec{\dot{\theta_{i} }}^{2}}{ \partial \dot{q_{k}} } )- \frac{\partial \frac{1}{2} \vec{ \dot{ \theta _{i} }}^{2}}{\partial q_{k}} ] )\) \(= \sum_{i=1}^{nc} (-\frac{d}{dt}( \frac{ \partial (\frac{1}{2} m_{i}* \vec{v_{G_{i}}}^{2} + \frac{1}{2} J_{G_{i}}* \vec{\dot{\theta_{i} }}^{2} }{\partial \dot{q_{k}}}) + \frac{\partial ( \frac{1}{2} m_{i}* \vec{v_{G_{i}}}^{2} + \frac{1}{2} J_{G_{i}}* \vec{\dot{\theta_{i} }}^{2} ) }{\partial q_{k}} ) \) \(= -\frac{d}{dt}( \frac{ \partial Ec_{total}}{\partial \dot{q_{k}}}) + \frac{\partial Ec_{total}}{\partial q_{k}} \)Llegamos entonces a:
\(Q_{in,k}= -\frac{d}{dt}( \frac{ \partial Ec_{total}}{\partial \dot{q_{k}}}) + \frac{\partial Ec_{total}}{\partial q_{k}} \)Al ser la ecuación que buscamos
\(Q_{k} + Q_{in,k} =0\)Una vez conocido el valor de \(Q_{in,k}\) podemos reescribirla como:
\(Q_{k} = \frac{d}{dt}( \frac{ \partial Ec_{total}}{\partial \dot{q_{k}}}) – \frac{\partial Ec_{total}}{\partial q_{k}} \)
Siendo \(Ec_{total}\) la energía cinética total de todo el sistema
Ahora necesitaríamos conocer el valor de \(Q_{k}\) , que es la componente perteneciente a las fuerzas externas.
En estas fuerzas entrarían las fuerzas elásticas, fuerza de la gravedad, fuerzas disipativas, fuerzas puntuales, momentos… En definitiva cualquier tipo de fuerza que modifique la energía del sistema.
La clave de usar este desarrollo es que podemos descomponer el cálculo de \(Q_{k}\) en función del tipo de fuerza que nos encontremos, de manera que tras clasificar las fuerzas sólo tendríamos que añadirlas a la fórmula.
Fuerzas conservativas
Un tipo de fuerzas que encontraremos en el problema serán las fuerzas conservativas. Estas fuerzas están caracterizadas por una función potencial tal que:
\(\vec{F}=-\vec{\nabla} V= -(\frac{ \partial V}{ \partial x },\frac{ \partial V }{\partial y})\)Básicamente encontraremos 2 fuerzas conservativas: Gravitatoria y elástica.
Potencial gravitatorio
Definiendo el potencial gravitatorio \(V_{g}=mgh\) (h es equivalente a y) se cumple que \(\vec{F_{g}}=(0,-mg)= -(\frac{ \partial V_{g}}{ \partial x },\frac{ \partial V_{g} }{\partial y}) \)
Potencial elástico
En el caso unidireccional se tiene que \(\vec{F_{el}}=-k \vec{ \bigtriangleup l}\)
Por lo tanto podemos definir el potencial elástico como \(V_{el}= \frac{1}{2}k (\bigtriangleup l )^{2}\)
Del mismo modo que en el caso de un muelle torsional se tiene que:
\(\vec{M_{el}}=-k_{T} \vec{ \bigtriangleup \theta}\) \(V_{el}= \frac{1}{2}k (\bigtriangleup \theta )^{2}\)Expresión de la componente del potencial
Expresaremos el potencial total como \(V=V_{g}+V_{el}\) resultante de todas las fuerzas potenciales sobre todos los cuerpos del sistema.
Recordemos que:
\(Q_{k} = \sum_{i=1}^{nc} \sum_{j=1}^{nf} (F_{x_{ij}} \cdot \frac{\partial x_{ij}}{\partial q_{k}} + F_{y_{ij}} \cdot \frac{\partial y_{ij}}{\partial q_{k}})\)Realizando la siguiente derivación aplicando la regla de la cadena:
\(\frac{\partial V}{ \partial q_{k}}= \frac{ \partial V}{ \partial x} * \frac{ \partial x}{ \partial q_{k}} + \frac{ \partial V}{ \partial y} * \frac{ \partial y}{ \partial q_{k}} =-(F_{x_{cons}}* \frac{ \partial x}{ \partial q_{k}} +F_{y_{cons}} * \frac{ \partial y}{ \partial q_{k}} )=-Q_{k_{cons}}\)Llegamos entonces a:
\(Q_{k_{nc}} – \frac{\partial V}{ \partial q_{k}} = \frac{d}{dt}( \frac{ \partial Ec_{total}}{\partial \dot{q_{k}}}) – \frac{\partial Ec_{total}}{\partial q_{k}} \)\(Q_{k_{nc}} = \frac{d}{dt}( \frac{ \partial Ec_{total}}{\partial \dot{q_{k}}}) – \frac{\partial Ec_{total}}{\partial q_{k}} + \frac{\partial V}{ \partial q_{k}} \)
Quedando únicamente por definir la parte correspondiente a las fuerzas no conservativas
Fuerzas viscosas: Amortiguador
Un caso especial de fuerzas disipativas es el del amortigüador viscoso. Este ejerce una fuerza disipativa igual a una constante por la velocidad de movimiento (O velocidad del incremento de posición), siendo:
\(\vec{F_{d}}=-r \vec{ \bigtriangleup \dot{l}} \)Observamos que es análogo a la fuerza elástica pero empleando la velocidad de elongación.
De este modo, podemos definir una función “potencial disipativa” \(D=\frac{1}{2}r \vec{ \bigtriangleup \dot{l}} \) tal que:
\(-\frac{\partial D}{\partial \dot{q}}=- r \bigtriangleup \dot{l} * \frac{\partial \bigtriangleup \dot{l} }{\partial \dot{q}}= \vec{F_{d}} * \frac{\partial \bigtriangleup \dot{l} }{\partial \dot{q}} = Q_{k_{dis}}\)Llegamos a:
\(Q_{k_{act}} – \frac{\partial D}{\partial \dot{q_{k}}} = \frac{d}{dt}( \frac{ \partial Ec_{total}}{\partial \dot{q_{k}}}) – \frac{\partial Ec_{total}}{\partial q_{k}} + \frac{\partial V}{ \partial q_{k}} \)\(Q_{k_{act}} = \frac{d}{dt}( \frac{ \partial Ec_{total}}{\partial \dot{q_{k}}}) – \frac{\partial Ec_{total}}{\partial q_{k}} + \frac{\partial V}{ \partial q_{k}} + \frac{\partial D}{\partial \dot{q_{k}}} \)
Componente de las fuerzas activas
Ahora sólo nos quedaría definir el valor de la componente perteneciente a las fuerzas que no son ninguna de las definidas anteriormente.
Siguiendo la definición de nuestras componentes;
\(Q_{k}=\frac{\delta \mathcal{L}}{\delta q_{k}}=\frac{\vec{F}* \delta \vec{despl}}{\delta q_{k}}=\vec{F}\frac{\partial \vec{\delta}}{\partial q_{k}}\)Que habría que calcularse manualmente introduciendo nuestra fuerza y la derivada del desplazamiento respecto a nuestro grado de libertad
Ecuaciones de Lagrange
Una vez definidos todos nuestros términos llegamos a la expresión general de las ecuaciones de Lagrange:
\( \frac{d}{dt}( \frac{ \partial Ec}{\partial \dot{q_{k}}}) – \frac{\partial Ec}{\partial q_{k}} + \frac{\partial V}{ \partial q_{k}} + \frac{\partial D}{\partial \dot{q_{k}}} = Q_{k} \)
Las cuales pueden emplearse para el caso de 1, 2 o n grados de libertad. En el caso de 1 grado de libertad la solución será automática. En el caso de varios grados de libertad, como el caso de un péndulo que además rota, podremos encontrarnos el caso de que las ecuaciones estén acopladas o no. Ya sería cuestión de emplear métodos matemáticos para la resolución de dichas ecuaciones.
Ejemplo: Bloque que vibra
Vamos a poner un ejemplo de uso de estas ecuaciones para el caso de una masa que vibra con una fuerza aplicada sobre la segunda masa:
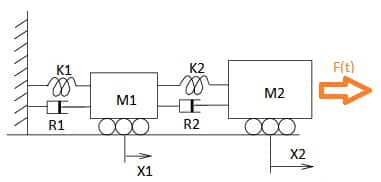
Tenemos 2 grados de libertad; el movimiento de la primera masa \(x_{1}\) y el movimiento de la segunda masa \(x_{2}\)
Nuestras ecuaciones serían:
\(Ec= \frac{1}{2}m_{1}\dot{x_{1}}^{2} + \frac{1}{2}m_{2}\dot{x_{2}}^{2} \) \(V= \frac{1}{2}k_{1}x_{1}^{2} + \frac{1}{2}k_{2}(x_{2}- x_{1}) ^{2} \) \(D= \frac{1}{2}r_{1} \dot{x_{1}}^{2} + \frac{1}{2}r_{2}(\dot{x_{2}}- \dot{x_{1}}) ^{2} \) \( Q_{k}=\frac{\delta \mathcal{L}}{\delta q_{k}}= \frac{\vec{F}(t)* \delta \vec{x_{2}}}{\delta q_{k}} =F(t) *\frac{\partial x_{2}}{\partial q_{k}}\)Escribiendo las ecuaciones de Lagrange para cada uno de nuestros grados de libertad:
\(x_{1} : \frac{d}{dt}( \frac{ \partial Ec}{\partial \dot{ x_{1} }}) – \frac{\partial Ec}{\partial x_{1} } + \frac{\partial V}{ \partial x_{1} } + \frac{\partial D}{\partial \dot{ x_{1} }} = Q_{1} \\ \) \(x_{2} : \frac{d}{dt}( \frac{ \partial Ec}{\partial \dot{ x_{2} }}) – \frac{\partial Ec}{\partial x_{2} } + \frac{\partial V}{ \partial x_{2} } + \frac{\partial D}{\partial \dot{ x_{2} }} = Q_{2} \)\(m_{1} \ddot{x_{1}} + r_{1} \dot{ x_{1} } + r_{2} \dot{ x_{1} } – r_{2} \dot{x_{2}} + k_{1} x_{1} + k_{2} x_{1} – k_{2} x_{2} = 0 \)
\(m_{2} \ddot{x_{2}} + r_{2} \dot{ x_{2} } – r_{2} \dot{x_{1}} + k_{2} x_{2} + – k_{2} x_{1} = F(t) \)
Y así obtenemos el sistema de ecuaciones diferenciales que, tras resolverlo, nos dará la solución de \(x_{1}(t), x_{2}(t)\) (No es nada difícil resolverlo)
Observamos que este procedimiento más formal nos ha simplificado mucho el problema, el cual mediante el uso de vectores y fuerzas de reacción nos hubiese llevado a la misma solución pero tras hacer más cálculos y probablemente equivocarnos con los signos.


6 comentarios en «Demostración de las Ecuaciones de Lagrange para estudiar el movimiento»