Teoría de la Elasticidad: Tensiones I

Artículo anterior:

Teoría de la Elasticidad: Introducción y conceptos previos

En este artículo profundizaremos en el concepto de tensión, entendiendo su significado físico, introduciendo el concepto de tensor de tensiones, y obteniendo las ecuaciones básicas que debe de verificar las componentes de dicho tensor para ser válido.

Imágenes tomadas del libro “Teoría de la Elasticidad” de Federico París, profesor de la ETSI .

Tabla de contenidos

Concepto de Tensión y Estado tensional

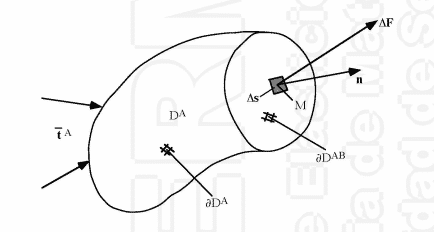
Como vimos en la introducción, en un cuerpo que se encuentra bajo diferentes tipos de fuerzas externas existe una serie de fuerzas internas que mantienen dicho cuerpo unido. Si virtualmente cortásemos el cuerpo en dos, observaríamos que cada sección ejerce sobre su opuesta una serie de fuerzas y momentos de igual magnitud pero sentido contrario que mantendrían las mitades estables.

Siguiendo la notación del dibujo y para permitir el equilibrio entre subdominios, en cada punto M de \(\partial D^{AB}\) con una normal \( \vec{n} \) unitaria exterior al subdominio \( D^{A}\) sobre una porción de área \( \bigtriangleup S \) existirá una distribución de fuerzas \( \bigtriangleup \vec{F} \).

Si tomamos un trozo infinitesimal de área \( \bigtriangleup S \to 0\) , podemos definir el vector tensión en cada punto M como:

\(\vec{T}=\lim_{\bigtriangleup S \to 0} \frac{\bigtriangleup \vec{F}}{ \bigtriangleup S} \ \ \ \ ;\ \ \ \ \frac{[N]}{[m^{2}]}=[Pa]\)

Observamos que tiene unidades de presión

El significado físico del vector tensión podría imaginarse como una especie de campo vectorial de presiones. A diferencia con la típica presión que es siempre normal a la superficie, esta tensión varía su dirección en cada punto de la superficie. Aunque a decir verdad, una forma muy sencilla de comprender este concepto es el de imaginarse una distribución de fuerzas (Cuerdas ancladas a la superficie que tiran de ella) pero con unidades de presión. El truquillo de estudiar fuerzas por unidad de área infinitesimal es que podemos asumir sin pérdida de generalidad que no existen momentos de reacción entre las superficies.

\( \vec{T} \) no tiene por qué coincidir en dirección con \( \vec{n} \) , pero depende de la normal que tomemos. Observamos que para cada punto del sólido (De los infinitos que existen) podemos cortar el sólido en dos mitades (De infinitas maneras). Esto nos lleva a la conclusión de que nuestro vector tensión tiene un dominio doblemente infinito y dicho dominio puede representarse como \(\vec{T}=\vec{T}^{n}(P)\)

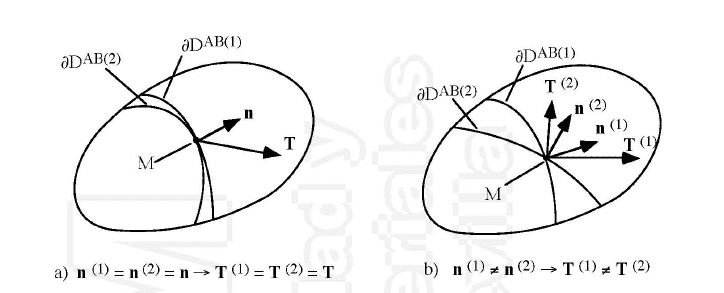
Foto mostrando que tensiones en el mismo punto pero asociadas a distintas normales tienen distinta orientación. — Tensiones en el mismo punto pero asociadas a distintas normales tienen distinta orientación.

Sin embargo, veremos un poco más adelante que podemos obtener el vector tensión asociado a un plano de normal cualquiera en un determinado punto a partir de conocer el estado tensional en dicho punto.

En lugar de estudiar la fuerza y momento total que ejerce una sección sobre la otra (En la parte de resistencia de materiales se hace así) estudiamos los esfuerzos que se ejercen por unidad de área infinitesimal, de manera que no se transmiten momentos)

Representación del vector tensión

Componentes intrínsecas

Podemos expresar el vector tensión de forma local mediante dos direcciones; Una paralela a la normal y otra que coincide con la proyección del vector tensión sobre la superficie.

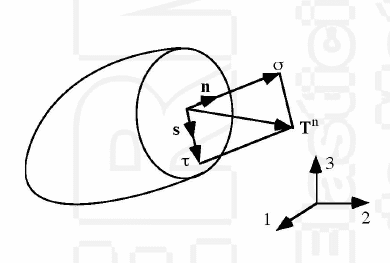
De esta forma:

\( \left \{ \begin{matrix} \sigma_{n}=\vec{T}*\vec{n} \\ \vec{\tau} = \vec{T}-\sigma_{n}*\vec{n} \end{matrix} \right.\)

Componentes globales

Como alternativa al sistema local, podemos expresar el vector tensión mediante el clásico sistema de referencia compuesto de 3 vectores ortonormales.

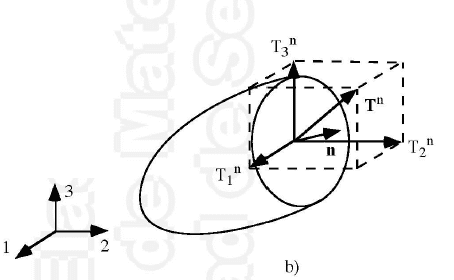
\(\vec{T} ^{n} =(T_{1} ^{n} , T_{2} ^{n} , T_{3}^{n}) \ \ \ , \ \ \ \{1,2,3\}\)

Componentes tensionales

Vamos a observar las tensiones generadas en un punto genérico M de nuestro cuerpo. Para facilitar la representación tomaremos un cubo infinitesimal con sus caras coincidentes con los planos de nuestro sistema de referencia.

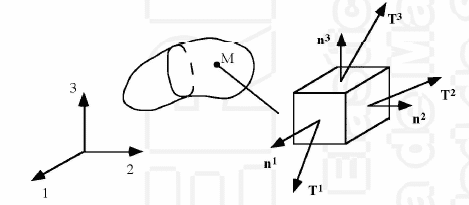
Cada cara tendrá una sección con su correspondiente normal exterior asociada y su vector tensión.

Recordamos que expresamos las componentes de cada vector tensión con la forma \(\vec{T}^{n}\) , tal que el subíndice marca la dirección y el superíndice marca la cara del cubo a la cual le pertenecen las tensiones:

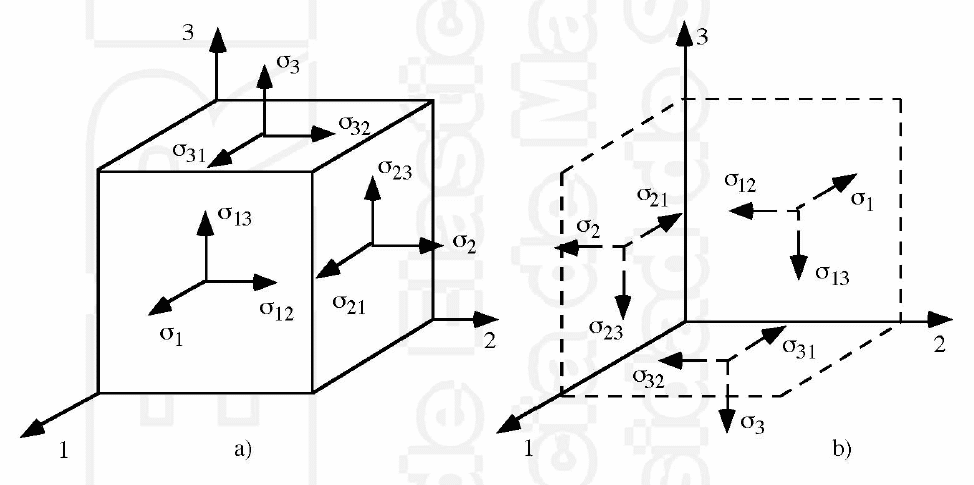
\(\vec{T}^{1} \left\{ \begin{matrix} T^{1}_{1}=\sigma_{11} \\ T ^{1}_{2} =\sigma_{12} \\ T ^{1}_{3} =\sigma_{13} \end{matrix} \right\}, \vec{T}^{2} \left\{ \begin{matrix} T^{2}_{1}=\sigma_{21} \\ T ^{2}_{2} =\sigma_{22} \\ T ^{2}_{3} =\sigma_{23} \end{matrix} \right\}, \vec{T}^{3} \left\{ \begin{matrix} T^{3}_{1}=\sigma_{31} \\ T ^{3}_{2} =\sigma_{32} \\ T ^{3}_{3} =\sigma_{33} \end{matrix} \right\} \)

\( \sigma_{ij} \left\{ \begin{array}{ll} i = \text{Cara} \\ j = \text{Direccion} \end{array} \right.\)

Debido al concepto de reacción que cada sección ejerce sobre su opuesta, en la parte de atrás de nuestra sección encontraremos tensiones de igual magnitud pero sentido opuesto.

De esta forma y para mantener el signo (Tracción hacia el exterior y compresión hacia el interior), representamos con valores positivos las componentes de tensión de esta forma:

Caras vistas y ocultas — Caras vistas a) y caras ocultas b)

El tetraedro de Cauchy

Si conocemos las componentes de tres vectores tensión asociados a tres planos perpendiculares, podemos conocer la expresión del vector tensión asociado a un plano de normal cualquiera
Lema de Cauchy

Como ya anticipamos antes, conociendo el estado tensional en un punto podremos conocer el vector tensión asociado a cualquier plano que pase por dicho punto. Y conocer el estado tensional implica conocer el valor de tres vectores tensión (Es decir, 9 componentes). De esta forma, nuestro dominio doblemente infinito (Infinitos puntos e infinitos posibles cortes) se reduce a un dominio infinito (Infinitos puntos) siempre que conozcamos el estado tensional de cada punto.

Pero, ¿Cómo caracterizamos el estado tensional? Introduciremos el Tetraedro de Cauchy

Vamos a considerar un punto con forma de tetraedro infinitesimal definido por las dimensiones \(dx_{1},dx_{2},dx_{3}\) y cuyas aristas coinciden con nuestros ejes.

La normal exterior a las caras principales coincidirá con nuestros ejes. La cara oblicua tendrá una normal exterior cuya dirección dependerá del valor de \(dx_{1},dx_{2},dx_{3}\)

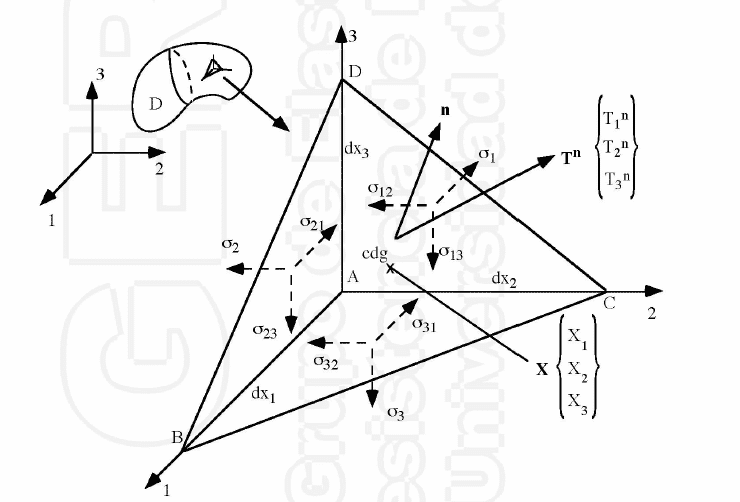
En cada cara tendremos un vector tensión asociado \((\vec{T}^{1}, \vec{T}^{2} , \vec{T}^{3} , \vec{T}^{n} )\)

Existen fuerzas por unidad de volumen \(\vec{X} \left \{ \begin{matrix} X_{1} \\ X_{2} \\ X_{3} \end{matrix} \right \} \)

Al encontrarse el tetraedro en equilibrio, la suma total de fuerzas debe de ser igual a cero en las 3 direcciones. El valor del área de la cara oblicua puede relacionarse con el área de cada una de las caras del tetraedro mediante su proyección tal que:

\(\boxed{dS_{i} = dS * n_{i}}\)

Vamos a hacer equilibrio de fuerzas en la dirección 1:

\(-\sigma_{11}*dS_{1} -\sigma_{21}*dS_{2} -\sigma_{31}*dS_{3} + T_{1}^{n}*dS + \frac{1}{6} X_{1} dx_{1} dx_{2} dx_{3} = 0\)

Despreciando las fuerzas de volumen al ser la resultante menor que las de área (Volumen infinitesimal \( \rightarrow \frac{1}{6} dx_{1} dx_{2} dx_{3} << dS_{i} = \frac{1}{2}dx_{a} dx_{b})\)

\(-\sigma_{11}*dS_{1} -\sigma_{21}*dS_{2} -\sigma_{31}*dS_{3} + T_{1}^{n}*dS= 0\)

Sustituyendo \(dS_{i} = dS * n_{i}\)

\(-\sigma_{11}*dS*n_{1} -\sigma_{21}*dS *n_{2} -\sigma_{31}*dS *n_{3} + T_{1}^{n}*dS= 0\) \(-\sigma_{11}*n_{1} -\sigma_{21}*n_{2} -\sigma_{31}*n_{3} + T_{1}^{n}= 0\)

Aplicando el mismo equilibrio para el resto de direcciones y agrupando términos:

\(\left\{ \begin{array}{l} \sigma_{11} \cdot n_{1} + \sigma_{21} \cdot n_{2} + \sigma_{31} \cdot n_{3} = T_{1}^{n} \\ \sigma_{12} \cdot n_{1} + \sigma_{22} \cdot n_{2} + \sigma_{32} \cdot n_{3} = T_{2}^{n} \\ \sigma_{13} \cdot n_{1} + \sigma_{23} \cdot n_{2} + \sigma_{33} \cdot n_{3} = T_{3}^{n} \end{array} \right. \rightarrow \left[ \begin{array}{ccc} \sigma_{11} & \sigma_{21} & \sigma_{31} \\ \sigma_{12} & \sigma_{22} & \sigma_{32} \\ \sigma_{13} & \sigma_{23} & \sigma_{33} \end{array} \right] \cdot \left[ \begin{array}{c} n_{1} \\ n_{2} \\ n_{3} \end{array} \right] = \left[ \begin{array}{c} T_{1} \\ T_{2} \\ T_{3} \end{array} \right] \)

Que, en forma compacta puede escribirse como \( \boxed{\sigma_{ji}*n_{j}=T_{i}} \ \ \ o \ \ \ [\sigma]*\vec{n}=\vec{T}\)

El tensor de tensiones

Representamos como \([\sigma]\) al tensor de tensiones \(\left [\begin{matrix} \sigma_{11} & \sigma_{21} & \sigma_{31} \\ \sigma_{12} & \sigma_{22} & \sigma_{32} \\ \sigma_{13} & \sigma_{23} & \sigma_{33} \end{matrix} \right ] \)

Es un tensor de segundo orden y caracteriza el estado tensional de un cuerpo. Cada una de las componentes \(\sigma_{ij}\) variará en función del punto que tomemos y conocer sus valores en todos los puntos del cuerpo nos permite calcular el vector tensión asociado a cualquier plano que pasa por cualquier punto.

Este es el principal objetivo de la Teoría de la Elasticidad; es decir, a partir de diversas hipótesis, simplificaciones y relaciones matemáticas obtendremos la forma de \([\sigma]\)

Equilibrio interno

Una vez establecida la relación entre el estado tensional de un cuerpo y su tensor de tensiones asociado, queremos establecer las condiciones necesarias que debe de cumplir dicho tensor de tensiones para ser válido de forma que el cuerpo se encuentre internamente equilibrado.

En el caso de actuar fuerzas de volumen X, la distribución de tensiones debe de variar en concordancia para satisfacer este equilibrio interno.

Vamos a estudiar la distribución de tensiones en el caso de un cubo infinitesimal. Al igual que con el tetrahedro, conocemos únicamente el tensor de tensiones asociado a las caras ocultas (No aparecen representadas para no colapsar el gráfico), y gracias a la naturaleza continua de nuestro medio, estimaremos el valor en las caras visibles. Además, debemos de considerar las fuerzas volumétricas.

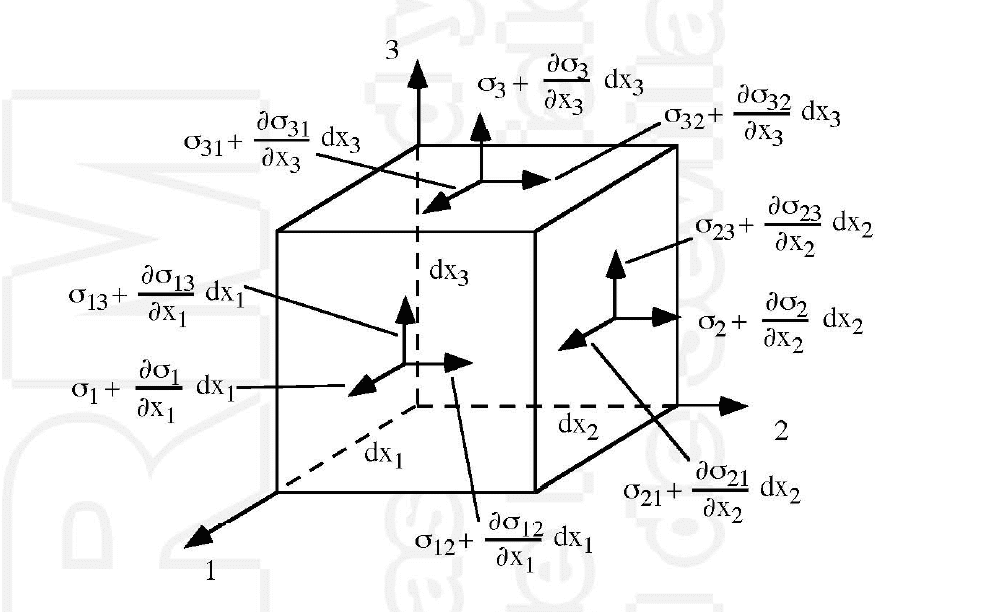
Cubo con ecuaciones de equilibrio interno

Una vez situadas todas las fuerzas, hacemos equilibrio de fuerzas en la dirección 1:

\((\sigma_{11} + \frac{\partial \sigma_{11} }{\partial x_{1}} dx_{1})dx_{2}dx_{3} – \sigma_{11}dx_{2}dx_{3} + \\ + (\sigma_{21} + \frac{\partial \sigma_{21} }{\partial x_{2}} dx_{2})dx_{1}dx_{3} – \sigma_{21}dx_{1}dx_{3} + \\ + (\sigma_{31} + \frac{\partial \sigma_{31} }{\partial x_{3}} dx_{3})dx_{1}dx_{2} – \sigma_{31}dx_{1}dx_{2} + \\ + X_{1}dx_{1} dx_{2} dx_{3} =0\)

Restando términos:

\(\dfrac{\partial \sigma_{11} }{\partial x_{1}} dx_{1}dx_{2}dx_{3} + \dfrac{\partial \sigma_{21} }{\partial x_{2}} dx_{2} dx_{1}dx_{3} + \dfrac{\partial \sigma_{31} }{\partial x_{3}} dx_{3} dx_{1}dx_{2} + X_{1}dx_{1} dx_{2} dx_{3} =0\)

Dividiendo entre \( dx_{1}dx_{2}dx_{3} \) y haciendo equilibrio en las direcciones 2 , 3:

\(\left\{ \begin{array}{l} \frac{\partial \sigma_{11}}{\partial x_{1}} + \frac{\partial \sigma_{21}}{\partial x_{2}} + \frac{\partial \sigma_{31}}{\partial x_{3}} + X_{1} = 0 \\ \frac{\partial \sigma_{12}}{\partial x_{1}} + \frac{\partial \sigma_{22}}{\partial x_{2}} + \frac{\partial \sigma_{32}}{\partial x_{3}} + X_{2} = 0 \\ \frac{\partial \sigma_{13}}{\partial x_{1}} + \frac{\partial \sigma_{23}}{\partial x_{2}} + \frac{\partial \sigma_{33}}{\partial x_{3}} + X_{3} = 0 \end{array} \right. \rightarrow \boxed{\frac{\partial \sigma_{ji}}{\partial x_{j}} + X_{i} = 0} \)

Siendo estas las ecuaciones de equilibrio interno, que debe de satisfacer el tensor de tensiones para que sea válido. Es decir, que el cuerpo se encuentra en “equilibrio estático” en su interior.

Equilibrio de momentos

Al igual que debe de existir un equilibrio de fuerzas para validar el estado de reposo, debe de existir también un equilibrio de momentos.

Vamos a tomar un cubo infinitesimal al igual que acabamos de hacer y le haremos un equilibrio de momentos en torno al eje 3:

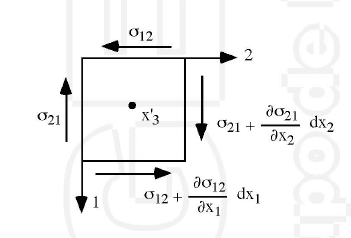
Tendremos en cuenta sólo los esfuerzos que generan momento. Aplicados en las caras y a una distancia del centro. Las fuerzas volumétricas se aplican en el centro y por lo tanto no generan momento.

\( \left( \sigma_{12} \cdot dx_{2} \cdot dx_{3} \cdot \frac{dx_{1}}{2} + \left( \sigma_{12} + \frac{\partial \sigma_{12}}{\partial x_{1}} \cdot dx_{1} \right) \cdot dx_{2} \cdot dx_{3} \cdot \frac{dx_{1}}{2} \right) \\ – \left( \sigma_{21} \cdot dx_{2} \cdot dx_{3} \cdot \frac{dx_{1}}{2} + \left( \sigma_{21} + \frac{\partial \sigma_{21}}{\partial x_{1}} \cdot dx_{1} \right) \cdot dx_{2} \cdot dx_{3} \cdot \frac{dx_{1}}{2} \right) = 0\)

Dividiendo entre \(dx_{1}dx_{2}dx_{3}\) y despreciando los términos infinitesimales llegamos a la relación

\(\sigma_{12} – \sigma_{21} = 0 \iff \boxed{\sigma_{12} = \sigma_{21}}\)

Lo que nos da un resultado IMPORTANTÍSIMO. Este resultado significa que nuestro tensor es simétrico, y por lo tanto de las 9 componentes incógnita sólo nos debemos de preocupar por 6 de ellas, reduciendo el número de ecuaciones necesarias.

Llegados a este punto haremos un resumen de las ecuaciones deducidas en este artículo y con los índices expresados para el caso de tensor simétrico. Hemos actualizado las fórmulas y el tensor de tensiones a la forma simétrica que es la que se usa. Así es más cómodo nombrar y memorizar el orden de las componentes del tensor de tensiones ya que i representa la fila y j la columna de la triangular superior.

Sumario

Tensor de tensiones

\(\left [\begin{matrix} \sigma_{11} & \sigma_{12} & \sigma_{13} \\ \sigma_{12} & \sigma_{22} & \sigma_{23} \\ \sigma_{13} & \sigma_{23} & \sigma_{33} \end{matrix} \right ] \)