Artículo anterior:
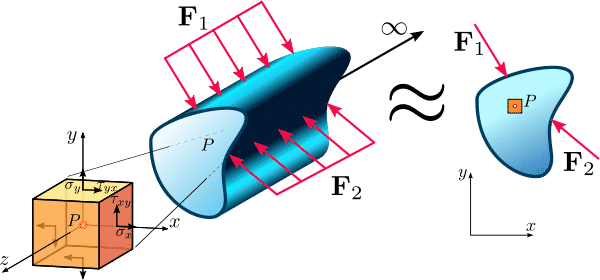
En este último artículo sentaremos las bases de la elasticidad plana. Es decir, aplicar todos los conceptos aprendidos en 3D a un sólido plano.
De primeras parece que simplemente consiste en eliminar una fila y columna de los tensores y aplicar los conceptos a un problema 2D. Sin embargo va más allá, tanto en las condiciones que debe de cumplirse y la relación entre los tensores, como en el ámbito de aplicación de esta simplificación; muchos cuerpos tridimensionales en la realidad pueden estudiarse suponiendo problema plano sin pérdida de validez y simplificando muchísimo las ecuaciones.
Tradicionalmente se coloca el eje z de tal forma que dicha coordenada se elimina y aparece un problema plano en (x,y). En base a ello haremos la notación.
Esto no es más que una breve pincelada acerca del problema plano, exponiendo las condiciones y ecuaciones. Como siempre, para más información, ejemplos y ejercicios, recomiendo el libro de París.
Deformación Plana
Dado un cuerpo relativamente largo y con infinitos planos de simetría entre las secciones de su longitud, podemos suponer que ninguna componente de los tensores depende de la variable longitudinal y que las deformaciones en dirección del eje es nula (Debido a infinita simetría).
Esta simplificación se puede usar en el caso de estudiar el comportamiento de una viga o de un túnel por ejemplo.
De la condición de deformación nula obtenemos que \(\epsilon_{xz} = \epsilon_{yz} = 0 = \sigma_{xz} = \sigma_{yz}\)
En la dirección normal: \(\epsilon_{zz} = \frac{1}{E}[\sigma_{zz}-\nu(\sigma_{xx}+\sigma_{yy})] = 0 \iff \boxed{\sigma_{zz} = \nu(\sigma_{xx}+\sigma_{yy})}\)
El valor del resto de deformaciones no varía:
\(\epsilon_{xx} = \frac{1}{E}[\sigma_{xx}-\nu(\sigma_{yy}+\sigma_{zz})]\) \(\epsilon_{yy} = \frac{1}{E}[\sigma_{yy}-\nu(\sigma_{xx}+\sigma_{zz})]\) \(\epsilon_{xy} = \frac{1+\nu}{E}\sigma_{xy}\)De la ecuación de equilibrio interno obtenemos directamente una condición que debe de cumplirse:
\(\frac{\partial \sigma_{zz}}{\partial z} + X_{z} = 0 \iff \boxed{X_{z}=0}\)Ya que ninguna magnitud debe de depender de la coordenada z.
Nuestros tensores resultan ser:
\([\epsilon]=\left [ \begin{matrix} \epsilon_{xx} & \epsilon_{xy} & 0 \\ \epsilon_{xy} & \epsilon_{yy} &0 \\ 0 &0 &0 \end{matrix} \right ] \ \ \ \ \ \ \ \ \ \ \ \ [\sigma]=\left [ \begin{matrix} \sigma_{xx} & \sigma_{xy} & 0 \\ \sigma_{xy} & \sigma_{yy} &0 \\ 0 &0 & \sigma^{*}_{zz} \end{matrix} \right ]\)
Tensión Plana
Dado un cuerpo plano y fino en el cual no existen fuerzas actuando en las caras planas, podemos suponer que se encuentra bajo tensión plana generalizada.
Las caras se encuentran libres de esfuerzos. Sin embargo, en el interior pueden que existan esfuerzos en la dirección plana. Lo que ocurre es que, por simetría y el bajo espesor del sólido, al hacer una media de los esfuerzos en la dirección plana obtenemos un valor nulo, y lo aplicamos en todo el espesor.
Este tipo de consideración puede emplearse para estudiar el comportamiento de una chapa por ejemplo.
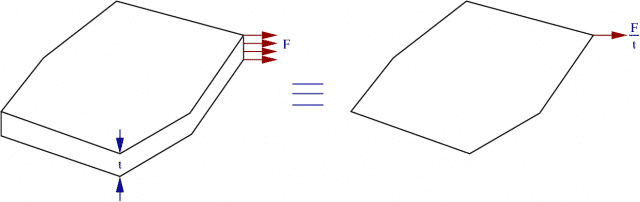
De la condición de tensión nula obtenemos que \(\sigma_{xz} = \sigma_{yz} = 0 = \epsilon_{xz} = \epsilon_{yz}\)
En la dirección normal: \(\sigma_{zz} = \frac{E}{1+\nu} \epsilon_{zz} + \frac{\nu}{1+\nu} (\sigma_{xx} + \sigma_{yy} ) = 0 \iff \boxed{\epsilon_{zz} = -\frac{\nu}{E}(\sigma_{xx}+\sigma_{yy})}\)
El valor del resto de deformaciones varía al eliminarse la tensión normal al plano:
\(\epsilon_{xx} = \frac{1}{E}[\sigma_{xx}-\nu\sigma_{yy}]\) \(\epsilon_{yy} = \frac{1}{E}[\sigma_{yy}-\nu\sigma_{zz}]\) \(\epsilon_{xy} = \frac{1+\nu}{E}\sigma_{xy}\)De la ecuación de equilibrio interno obtenemos directamente una condición que debe de cumplirse:
\(\frac{\partial \sigma_{zz}}{\partial z} + X_{z} = 0 \iff \boxed{X_{z}=0}\)Ya que hemos dicho que \(\sigma_{zz}=0\)
Nuestros tensores resultan ser:
\([\epsilon]=\left [ \begin{matrix} \epsilon_{xx} & \epsilon_{xy} & 0 \\ \epsilon_{xy} & \epsilon_{yy} &0 \\ 0 &0 & \epsilon^{*}_{zz} \end{matrix} \right ] \ \ \ \ \ \ \ \ \ \ \ \ [\sigma]=\left [ \begin{matrix} \sigma_{xx} & \sigma_{xy} & 0 \\ \sigma_{xy} & \sigma_{yy} &0 \\ 0 &0 & 0 \end{matrix} \right ]\)

![[Elasticidad y Resistencia de Materiales] Teoría de la Elasticidad Portada-elasticidad-alta](https://ingenieriabasica.es/wp-content/uploads/2020/07/Portada-elasticidad-alta-200x136.jpg)