Cuando un refresco no se encuentra lo suficientemente frío, recurrimos a los cubitos de hielo para disminuir aún más la temperatura del líquido. ¡Y funciona a la perfección! A los pocos segundos el vaso se encuentra frío a cambio de que se nos «agüe» un poco el refresco. Pero por supuesto que renta.
El hecho de que se agüe la bebida me dio por pensar en métodos alternativos para enfriar una bebida sin dejar agua, como puede ser el emplear cubitos metálicos (Clásicas piedras de whisky) o incluso el clásico hielo seco. Porque… ¿Por qué enfriar la bebida con algo que se derrite y altera el sabor? La respuesta inmediata es por el hecho de que el hielo es desechable y económico. Pero… ¿Eso es todo?
El título del artículo nos hace pensar que va dirigido a un niño de 4 años que no sabe que si mezclas algo frío con algo caliente, al final el calor se reparte y se alcanza un equilibrio térmico (Principio 0 de la termodinámica).
Pero ese no es el caso. Se acerca un momento histórico, un antes y un después en la vida de la gran mayoría de los lectores que han vivido engañados durante toda su vida… El hielo NO ENFRÍA porque es algo «frío» que cede calor al líquido. El hecho de que se enfría la bebida no se debe a la transferencia de temperatura, sino a la absorción de calor al derretirse el hielo.

Es muy fácil decirlo pero no tanto demostrarlo. Cualquier cosa que se diga sin cuentas y números por delante, debe de cogerse con pinzas. En este artículo voy a demostrar como siempre en lenguaje matemático y empleando las leyes básicas de la física que esto sucede de esta manera y que no hay opción a duda.

El Calor Latente
En el artículo hemos mencionado una transferencia de calor debido a la diferencia de temperatura (Transferencia de calor por convección) y una absorción de calor debido al cambio de fase (Calor latente).
El primer concepto es lógico e intuitivo. Sin embargo, el segundo concepto es algo que la gran mayoría no sabe. Supongamos un cubito de hielo que se encuentra a -20ºC en equilibrio térmico. Lo sacamos con unas pinzas, y empezamos a calentarlo con un mechero. La evolución de la temperatura del hielo será como indica el diagrama de calor latente:
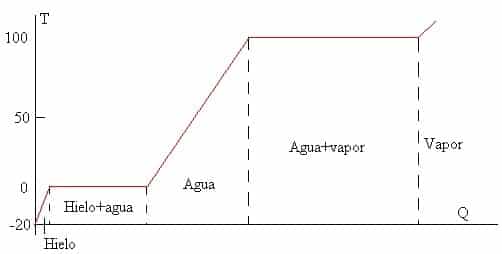
Al principio, antes de llegar al punto de fusión, el hielo será puramente hielo e irá aumentando su temperatura a medida que lo calentamos. Una vez alcance los 0 ºC (Punto de fusión), la temperatura del hielo se mantendrá en 0 ºC y en vez de calentarse, se derretirá. Una vez que todo el hielo se haya derretido, entonces el agua seguirá aumentando su temperatura hasta ocurrir lo mismo con el vapor.
Pero… ¿Por qué sucede esto? ¿Por qué en vez de aumentar la temperatura del hielo, ocurre un cambio de fase?
En el artículo hablando de la técnica de cocina del Baño María para fundir chocolate empleamos el mismo concepto pero en el tramo de líquido-vapor, estudiando el punto de ebullición en vez del punto de fusión:
Cuando una sustancia alcanza su punto de ebullición quiere decir que sus moléculas ya están listas para romper los enlaces y escapar. En este caso, necesitan un empujón extra de energía o, más bien calor, denominado calor latente. A partir de este punto toda la energía que la sustancia reciba no la empleará para aumentar la energía cinética de sus moléculas (Lo que aumentaría la temperatura), sino en romper los enlaces y escapar. Durante un cambio de fase la temperatura siempre permanece constante.
La ciencia detrás del Baño María
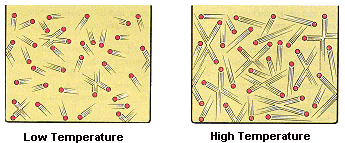
La temperatura es una medida de la energía cinética de las moléculas, es decir, del movimiento de las moléculas. Cuando calentamos un hielo que se encuentra por debajo de los 0 ºC lo que hacemos es inducir «vibraciones» en sus moléculas. A partir de los 0 ºC, la vibración de las moléculas es más fuerte que los enlaces que las mantiene en estado sólido, de manera que el calor extra que se vaya absorbiendo se empleará en romper enlaces en vez de aumentar aún más las vibraciones.
Podríamos imaginarnos los cubitos de hielo como «baterías» que mantienen el refresco a 0 ºC y que, cuando se derriten, es como si se hubiese agotado la batería y el refresco vuelve a calentarse.
Calor debido a convección y al cambio de fase
Ahora sí que sí, nos metemos en materia. Vamos a ver para un cubito de hielo de cierta masa que parte a una determinada temperatura, cuanto calor absorbe debido a la temperatura y cuanto calor absorbe por cambio de fase.
La transferencia de calor por convección dada por la Ley de enfriamiento de Newton es:
\({\displaystyle {\frac {dQ}{dt}}=h*A_{h}(T_{f}-T_{h})}\)Sin embargo, a nosotros no nos interesa conocer en detalle la evolución de temperatura y cómo se transmite al medio, sino que nos interesa únicamente el calor absorbido debido al aumento de temperatura del hielo.
En este caso entra en juego el denominado Calor específico, que se define como la cantidad de calor que hay que suministrar a una unidad de masa de una determinada sustancia para elevar su temperatura en un grado. Como curiosidad, el valor de 1 caloría se establece en la cantidad de calor necesario para producir un incremento de temperatura de 1 °C en una masa de 1g de agua desde 14,5 ºC hasta 15,5 ºC. Es por ello que el calor específico del agua es aproximadamente de 1 cal/(g * °C). 1 caloría es equivalente a 4,18 Julios (Unidad de energía empleada en el sistema internacional y relacionada con el concepto de trabajo mecánico), siendo el calor específico del agua 4180 J/(Kg * ºC)
El calor específico del hielo, expresado en Julios es de:
\(Cp = 2090 \ \frac{J}{kg * ºC}\)Es decir, que la fórmula para calcular el calor absorbido por un hielo a temperatura inicial \(T_{h}\) que absorbe calor hasta llegar a los 0 ºC es de:
\(Q=Cp * m * T_{h}\)Por otro lado, el calor absorbido para producir el cambio de fase viene dado por:
\(\bigtriangleup Q = \bigtriangleup m * L_{f}\)Siendo \(L_{f}\) el calor latente de fusión, que tiene una definición similar a la del calor específico. El calor latente de fusión del hielo es de \(334000 \ \frac{J}{kg}\). Observamos que es enormemente mayor al calor específico, aunque para comparar realmente el calor absorbido debemos de tener en cuenta la masa y la temperatura inicial.
Cálculo aproximado para cubito de hielo
Más o menos ya nos hacemos una idea de la cantidad de calor que absorbe el hielo debido al cambio de temperatura y debido al cambio de fase, y prematuramente podemos asegurar que la debida al cambio de fase es mucho mayor. Vamos a hacer las cuentas para el caso del típico cubito de hielo: Aproximadamente de 60g, que se encuentra en un congelador a -20ºC.
No nos hace falta conocer la cantidad de refresco a enfriar, ni su coeficiente de convección, ni siquiera su temperatura inicial. Todos esos datos serían las condiciones de contorno para resolver el problema de «transmisión de calor», conociendo en todo detalle el tiempo empleado en enfriar el refresco, la evolución y distribución de temperatura en función del tiempo y zona del refresco…
A nosotros lo que nos interesa conocer es el valor de los calores absorbidos, y para ello basta con emplear las ecuaciones escalares descritas anteriormente:
- \(Q_{Temp}=Cp * m * T_{h}\)
- \(Q_{fus} = m * L_{f}\)
Siendo \(Q_{total}=Q_{Temp} + Q_{fus}\) el calor total absorbido cuando el cubito de hielo se haya derretido totalmente.
\(Q_{Temp}=2,090 \ \frac{J}{g * ºC} * 60 g * 20 ºC = 2508 J\) \(Q_{fus} = 60 g * 334 \ \frac{J}{kg} = 20040 J\)Lo que nos lleva a \(\rightarrow \frac{Q_{fus}}{Q_{Temp}} \approx 8 \ ; \), es decir, que el calor absorbido por la fusión del hielo representa 8 veces el calor absorbido por la transferencia de calor.
Vamos a ir un paso más adelante. Y es el querer calcular el calor de un cierto volumen de agua (Aproximación de un refresco) que debe de absorber un cubito de hielo para poder bajar su temperatura hasta los 0ºC.
Según lo leído en este artículo, hemos dicho que un cubito de hielo no puede existir a más de 0 ºC (En condiciones normales), y por lo tanto se mantiene a esa temperatura mientras se derrite. Es por ello que, podemos asumir que en un mundo ideal (Transferencia de calor casi instantánea), un refresco con hielo abundante en equilibrio térmico debería de situarse en los 0ºC. En la realidad no es así y realmente el refresco se encuentra en unos 5 ºC aproximadamente. No obstante, empleando mucho hielo picado (Caso de los cócteles por ejemplo) se alcanzan los 0 ºC en el líquido ya que hay mucho hielo y se encuentra repartido.

El calor específico del agua hemos dicho que es de \(Cp = 4180 \ \frac{J}{kg * ºC}\), como vemos casi el doble que el del hielo.
Vamos a suponer un vaso de agua de unos 200 ml ~ 200 g que se encuentra a una temperatura ambiente de unos 20 ºC aproximadamente que queremos enfriar con un hielo. La pregunta es… ¿Cuánto calor deberá ser absorbido en condiciones ideales? ¿Podrá un cubito de hielo bajar su temperatura sin derretirse? Vamos a hacer las cuentas:
\(Q=4,18 \ \frac{J}{g * ºC} * 200 g * 20 ºC = 16720 J\)Es decir, un calor mucho mayor al absorbido por el cubito de hielo. De hecho, necesitaríamos 16720/2508 ~ 6 o 7 cubitos de hielo para enfriar la bebida sin que se derritiesen. Por este motivo, los típicos hielos metálicos no son muy efectivos para enfriar (Al menos grandes cantidades de líquido).
La cantidad de hielo que debería derretirse para bajar la temperatura se obtiene de la siguiente forma:
\(Q=16720 J = Q_{Temp}+\bigtriangleup Q_{fus} = 2508 + \bigtriangleup m * 334 \rightarrow \boxed{\bigtriangleup m \approx 42,55g}\)Es decir, que en un entorno ideal con paredes completamente aislantes y tras un tiempo infinito, el refresco alcanzaría 0 ºC al mismo instante que se derritiese la última pizca de hielo si usásemos 42,55 gramos de hielo (Para las condiciones dadas de 200g de agua, hielo a -20ºC y agua inicialmente a 20ºC)
Si en equilibrio se encuentra la mezcla a 0 ºC , ¿Por qué no se congela el agua?
Hemos dicho que la mezcla en equilibrio térmico de cubito de hielo derritiéndose en agua es de 0 ºC en condiciones ideales. Entonces, ¿Por qué no hay aunque sea una pequeña parte de agua que se congele?
La respuesta es fácil de decir pero difícil de comprender, y viene dada por el 2º principio de la termodinámica. Realmente que el hielo se derrita en vez de bajar su temperatura se debe al concepto de entropía, que bajo mi propia definición, diría que es como una especie de potencial o «fuerza divina» que marca qué camino siguen los procesos termodinámicos. Es por ello que lo caliente va a lo frío y no al revés, que si mezclamos varios colores luego no podemos separarlos con la misma facilidad, que si tiramos al suelo un vaso de cristal se romperá en pedazos pero si tiramos al suelo muchos pedazos no obtendremos un vaso… En definitiva que «la naturaleza tiende al desorden«.

La naturaleza favorece que el hielo se derrita y no lo contrario, y por este motivo el hielo tenderá a derretirse hasta que sólo tengamos agua (A grandes rasgos sería básicamente porque si la única fuente de absorción de calor es el hielo que se encuentra a 0 ºC, el agua no puede enfriarse más y por lo tanto no se congela).
En cierta manera, el agua en estado sólido presenta una estructura cristalina que representa cierto orden. Es por ello que de forma natural el agua tiende a estado líquido (Más desordenado), y realmente es necesario forzar la absorción del calor para convertirlo en hielo y no al revés. Es un concepto muy interesante pero demasiado extenso para ser explicado aquí. Estas son unas breves pinceladas de algo tan apasionante y trascendental como es la termodinámica, aplicable en numerosas situaciones de la vida cotidiana y extrapolable a otras disciplinas.
Si al igual que a mi, te parece muy curioso el hielo, no te pierdas este artículo:



Es un gran blog, una buena idea compartir estos enfoques con otros. Además, no hay mejor manera para aprender que intentar explicarlo, verdad?
Exacto Manuel. Cuando escribo los artículos tengo una idea del tema pero al buscar la forma de explicarlo es cuando llego a comprenderlo a la perfección. Un saludo!