En Minecraft nos encontramos caballos con atributos al azar dentro de un rango: vida, velocidad y salto. Si queremos el caballo con los mejores atributos (caballo perfecto) tenemos que mezclarlos para obtener una cría con una media de ambos caballos + una cierta aleatoriedad.

Siendo \(x_{A}\) y \(x_{B}\) un atributo (vida, por ejemplo) de los caballos A y B respectivamente, la vida que tendrá la cría seguirá la siguiente fórmula:
\(x=\dfrac{ x_{A}+ x_{B} + x_{C} }{3}\)
Siendo \(x_{C}\) la vida que tendría un caballo aleatorio, intentando simular el comportamiento real de los animales (hereda casi todo + existen ciertas mutaciones o variaciones). Lo mismo aplicado para el salto y la velocidad.
La presencia de esta relación matemática y de la estadística existente me ha impulsado a realizar un estudio que analice cosas como cuánto puede tardarse en obtenerse el caballo perfecto, cómo evolucionan los valores y cómo optimizar su obtención.
Es un artículo fuera de lo normal en este blog, y lo que quiero mostrar es la aplicabilidad práctica de las matemáticas en muchos ámbitos cotidianos como puede ser en un videojuego para niños.
Rango de valores y distribución estadística
Los valores mínimos, máximos y medios de cada atributo se muestra en la siguiente tabla:
| Mínimo | Medio | Máximo | |
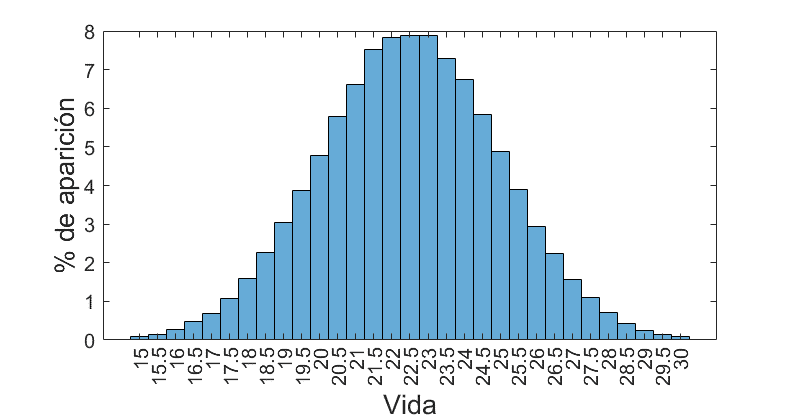
| Vida | 15 | 22.5 | 30 |
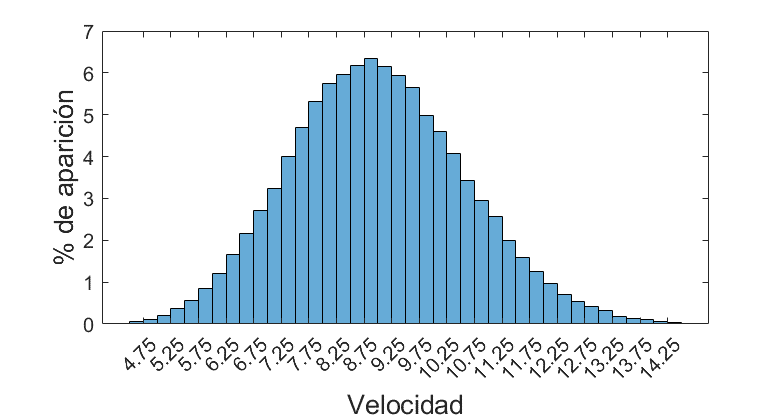
| Velocidad | 4.74 | 9 | 14.23 |
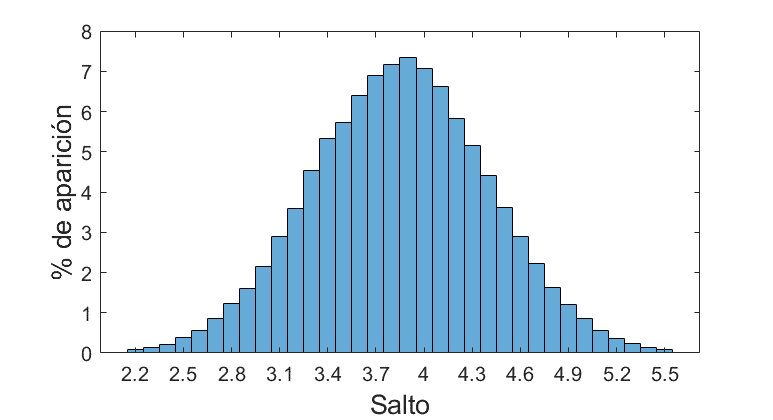
| Salto | 2.2 | 3.85 | 5.5 |
Esos son los únicos valores que nos proporciona la wiki oficial de Minecraft; sin embargo nos falta por saber bajo qué distribución estadística se generan. Lo más común es emplear una distribución gaussiana ya que estaremos probablemente en lo cierto gracias al teorema central del límite. Sin embargo, opté por emplear una distribución de Pearson.
Sólo para nerds: los valores están acotados por los extremos y además son finitos (cada 0.5 la vida y 2 decimales en velocidad y salto). Además, se ve que la vida y el salto tienen una media correcta. Sin embargo, la velocidad presenta una media que no se encuentra en el valor intermedio (el cuál entre 14.23 y 4.74 debería ser 9.485), lo que implica la necesidad de generar una distribución sesgada (skewed). Para estandarizar la distribución en todos los atributos no es compatible una gaussiana por lo que una Pearson con curtosis de 3 la sustituye perfectamente.
La representación de la distribución de los atributos se muestra a continuación:
Simulación
Partiendo de 2 caballos aleatorios, vamos a simular la evolución de las estadísticas a medida que los vamos mezclando. Como es lógico, en nuestro mundo de Minecraft haríamos los siguiente:
- Mezclamos dos caballos de atributos conocidos
- Identificamos los atributos de la cría
- Si la cría tiene peores atributos (o uno peor en concreto) -> La sacrificamos y volvemos a mezclar los padres
- Si la cría tiene mejores atributos (o uno mejor en concreto) -> Sacrificamos al peor de los padres y mezclamos la cría con el otro padre
- Repetimos
Si queremos tener el caballo perfecto, entonces debemos de hacer una media ponderada de cada uno de los atributos y establecer una puntuación global al caballo. Los caballos de mayor puntuación global son los que debemos mezclar.
Un caballo de atributos (20,2.5,11) tendría una puntuación de (20-15)/15 + (2.5-2.2)/3.3 + (11-4.74)/9.5 = 1.083
Un caballo de atributos (29,2.2,6) tendría una puntuación de 1.066
Un caballo perfecto sería un 3, y un caballo con valores medios tendría un 1.5
Si queremos tener el caballo más veloz tendríamos que centrarnos únicamente en el atributo de velocidad, mezclando los caballos con mayor velocidad (pero esto implica tener valores mediocres en vida y salto). La ventaja de centrarnos en un aspecto en concreto es que es más rápido maximizarlo (como se verá a continuación.
Simulación caballo perfecto
A continuación se muestra la evolución de las estadísticas del mejor caballo en cada una de las iteraciones (mejor caballo entre padre A, padre B y cría justo antes de sacrificar al peor) así cómo cuantas iteraciones hemos empleado en alcanzar diferentes puntuaciones. Para ello partimos de 2 caballos de atributos generados al azar que vamos combinando siguiendo el algoritmo anterior.
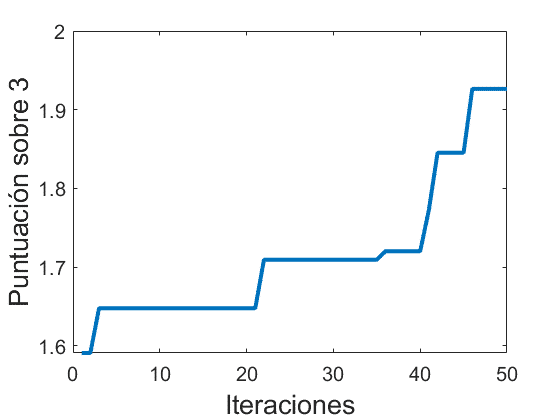
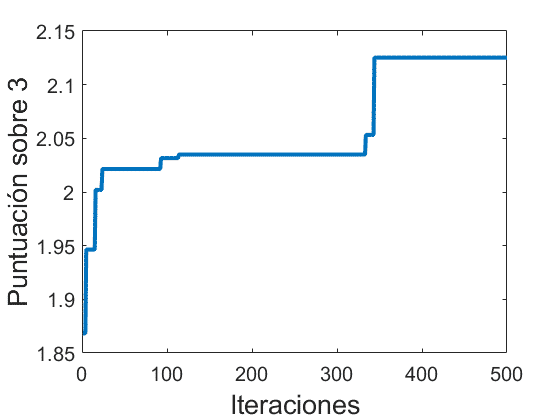
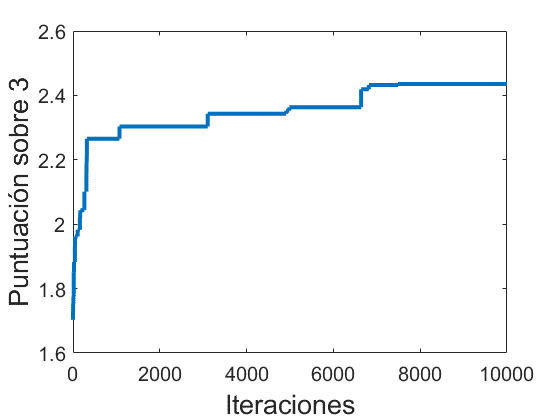
Se observa como para un número de mezclas manuales razonables para un jugador (50) se alcanza cerca de 2/3 o lo que es lo mismo un caballo al 66.66% (25 de vida, 4.76 de salto y 11.08 de velocidad) mientras que tras un elevadísimo número de simulaciones (10.000) el mejor caballo resulta alrededor del 80%, siendo prácticamente una asíntota obtener el caballo perfecto.
El principal problema es que cada vez necesitamos que la aleatoriedad nos genere un tercer caballo (caballo c) casi perfecto para poder subir las estadísticas de nuestro caballo cría, pero encima cada vez que esto rara vez sucede los atributos se diluyen y es necesario esperar hasta que obtengamos otra vez un tercer caballo buenísimo para volver a diluirlo y así sucesivamente, limitando enormemente la capacidad de generar el caballo perfecto.
Si lo que hacemos es simular que cada vez que tenemos una cría encontramos un caballo salvaje (caballo generado aleatoriamente con atributos únicos, no diluidos) y a su vez en cada iteración sustituimos el antiguo caballo salvaje por uno nuevo si el nuevo es mejor que el anterior obtenemos la siguiente evolución:
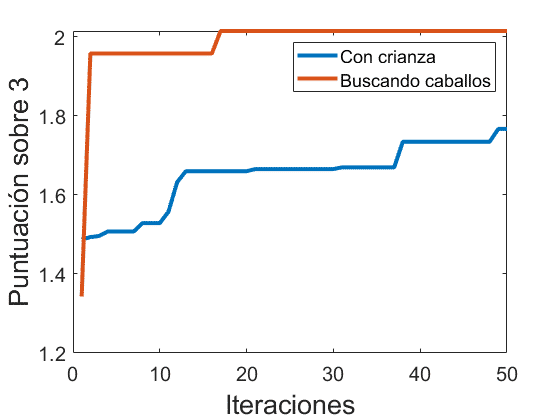
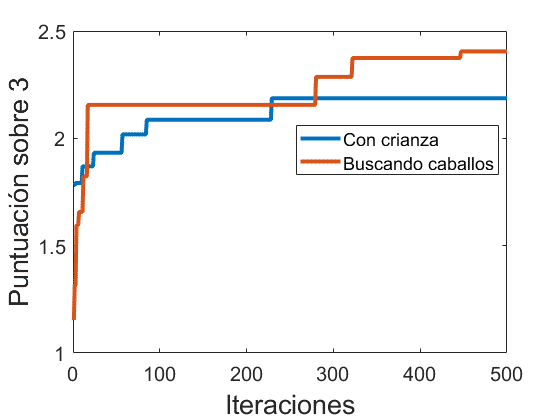
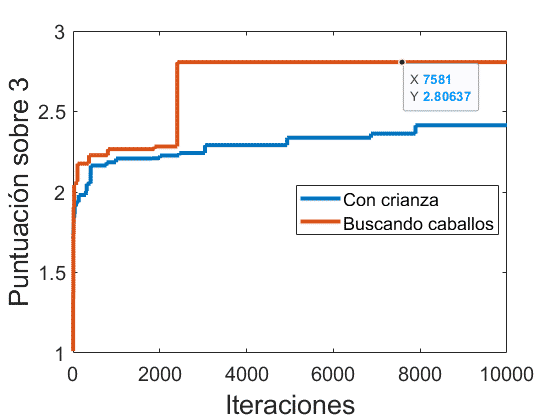
Es decir, que si quisiésemos buscar el mejor caballo o el caballo más cercano al perfecto (porque ya se ha demostrado que mezclando el perfecto es imposible al existir asíntota), no tendríamos que mezclar los mejores caballos entre sí sino buscar caballos salvajes hasta encontrar uno casi perfecto. Esto, sin embargo, no es tan fácil puesto que los caballos no son fáciles de encontrar, son limitados y más aún en servidores públicos. Hay que elegir entre comodidad o exploración.
Simulación máxima velocidad
Vamos a realizar, bajo las mismas condiciones que en el apartado anterior, el cálculo del número de iteraciones medias necesarias para obtener el caballo con la máxima velocidad posible así como la evolución de los valores.
Para ello lo que buscaremos maximizar será única y exclusivamente el atributo de velocidad, no prestando atención al resto de atributos. El resultado se muestra a continuación:
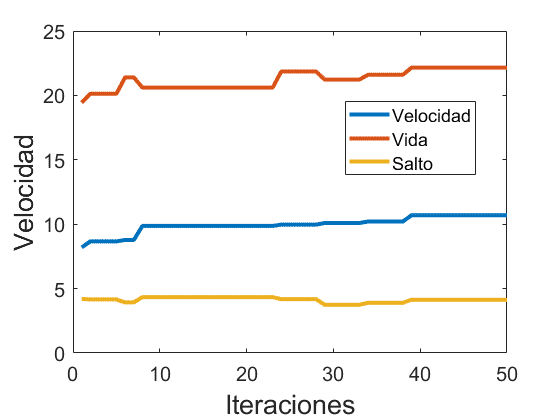
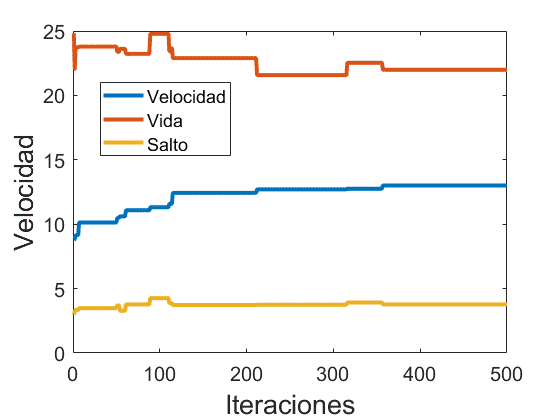
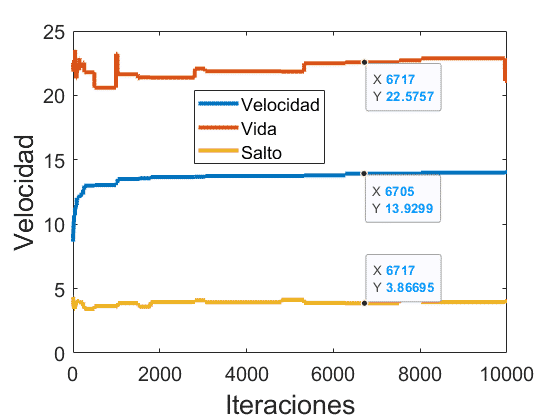
Se observa cómo en este caso es mucho más factible maximizar sólo un atributo que el conjunto de ellos como pasaba en el caso anterior. Esto se debe porque si por ejemplo para obtener un caballo aleatorio al 100% de velocidad la probabilidad es de un 1% (es un ejemplo), la probabilidad de un caballo aleatorio al 100% de velocidad y salto es del 0.1% y a su vez un 0.01% los tres atributos a la vez. La tendencia siempre va a ser a obtener atributos cercanos a la media y, en el caso de obtener valores extremos en alguno de los atributos, lo más probable es que el resto de atributos se encuentren en la media.
Esta última observación se pone de manifiesto en el resultado final, donde hemos podido lograr casi un 98% de velocidad máxima y lo que sucede con los valores de vida y salto no es que aumenten o disminuyan, sino que tienden a la media.
En conclusión se ofrecen los siguientes consejos:
- Es más probable y fácil encontrar un caballo casi perfecto salvaje que crearlo con mezclas
- Un caballo con atributos medios al 60-70% está bastante bien, es difícil mejorarlo
- Es posible maximizar un atributo en concreto y de hecho lo aconsejable es maximizar exclusivamente la velocidad porque a la larga se tendrá vida y salto medio, los cuales son aceptables y suficientes (no te hace falta saltar más de 4 bloques ni hace falta tanta vida ya que podemos aumentarla con una armadura)




