Varios son los países que se disputan el podio de países con mayor longitud de costa. Sin embargo, si buscamos en la Wikipedia el ranking de países por longitud de costa vemos como por ejemplo Noruega según «The World Factbook» tiene el segundo lugar pero según «World Resources Institute» baja hasta el séptimo lugar.
¿Cómo es posible? Por qué sucede eso si… al fin y al cabo mides la costa y punto… ¿No?
Pues la respuesta viene dada por el título del artículo. Porque NO se puede medir con exactitud la longitud de costa de un país. Pueden darse unas estimaciones basadas en unas normas estandarizadas, pero nunca conocer la longitud exacta. Y la discrepancia, como puede observarse, de usar unas normas u otras puede suponer contabilizar ±30.000 kilómetros…
La Paradoja de la línea de costa
El concepto de longitud tiene su origen en la distancia euclidiana. En la geometría euclidiana habitual, la distancia entre dos puntos se mide según una línea recta que a su vez representa la distancia más corta entre ambos puntos. Medir con exactitud longitudes de arco de determinadas curvas geométricas ya es algo más complicado. Sin embargo, es posible.
La longitud de una curva suave puede aproximarse midiendo por medio de pequeños segmentos que se adaptan a su curvatura. Cuantos más abruptos sean los cambios de curvatura, menor debe de ser la «regla» con la que medimos, y lo que sucede es que cuanto más pequeña es nuestra regla más nos acercamos a la longitud real hasta llegar a una especie de asíntota donde resulta que tomar medidas más pequeñas no afecta sensiblemente al resultado obtenido, siendo ese valor estable la longitud de dicha curva. En el caso de una circunferencia es fácil obtener una fórmula de la longitud en función del ángulo que se recorre ya que su curvatura es constante.
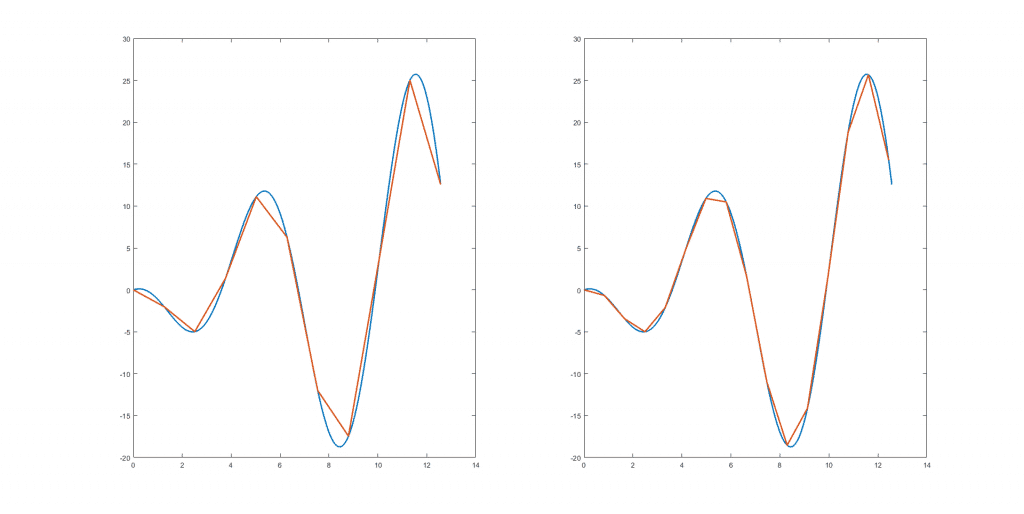
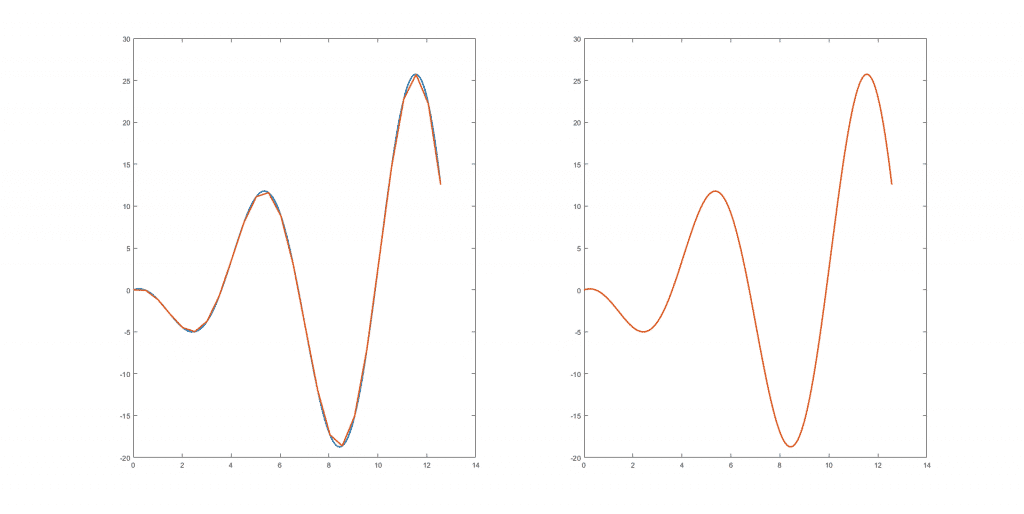
Sin embargo, no todas las curvas se pueden medir de este modo. Se define un fractal como una curva cuyo grado de complejidad no se reduce al mejorar la escala empleada para representarla. A diferencia de lo que ocurre con las curvas suaves en las que las aproximaciones mejoran al aumentar la precisión de la escala y tienden a un valor fijo, el valor medido en sucesivas aproximaciones en una curva fractal puede cambiar bruscamente.

De hecho, la longitud de un fractal ideal siempre tiende a infinito. La costa de un país, si bien no es un fractal perfecto, es una curva con bastante irregularidad. Y esta irregularidad es aún mayor en costas como la de Gran Bretaña o Noruega.
Supongamos que queremos medir la longitud de costa de Gran Bretaña. Comenzamos empleando reglas más o menos grandes y las vamos haciendo más pequeñas para adaptarnos mejor a la línea de costa. Lo que se observa es que, a medida que disminuimos el tamaño de nuestra regla, más distancia estamos midiendo. De hecho, surge entonces el problema de limitar la longitud de nuestra regla. ¿Mediría la misma distancia un coche que recorriese la costa que un ser humano con un odómetro? ¿Y un perro? ¿Y una hormiga? La hormiga tendría en cuenta incluso los recovecos entre las piedras…
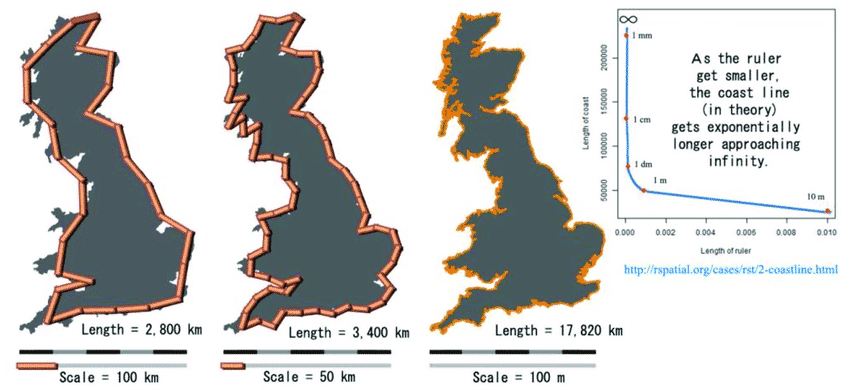
Por dicho motivo no existe un valor exacto de la longitud de costa de un país y lo que existe son mediciones en base a unos criterios homogéneos que garantizan una aproximación «equitativa» para todos los países.
Sin embargo, sí que se puede medir con bastante precisión la superficie de un país. ¿Cómo es eso posible?
Medición de la superficie de un país
Para medir la superficie de un país hay muchos métodos. El que se me ocurre ahora mismo más exacto podría ser tomar coordenadas de diferentes puntos alrededor de la frontera/costa y teniendo en cuenta la curvatura de la tierra calcular el área contenida entre dichos puntos como si de una envolvente conexa se tratase.
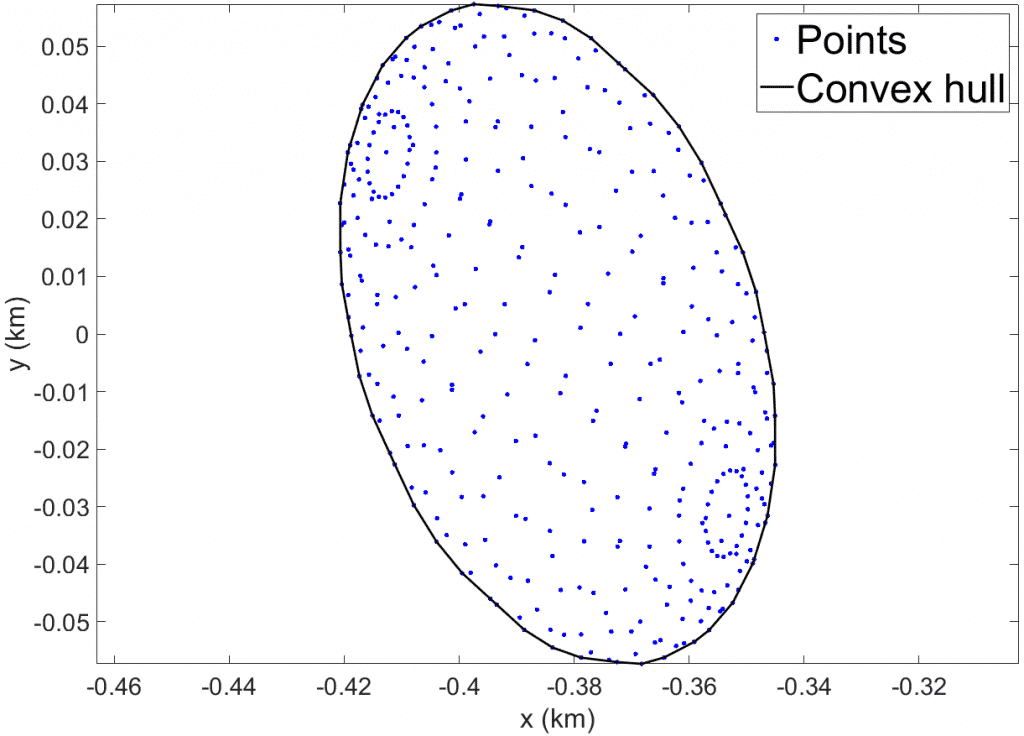
Otra idea menos sofisticada pero que es lo que suele hacerse es rellenar la superficie del país con formas geométricas de área conocida (triángulos, cuadrados, rectángulos) y simplemente emplear versiones de estas más pequeñas en aquellas zonas de los bordes donde la curvatura no permite emplear una forma geométrica tan grande. Es un poco como lo que se hace en el método de los elementos finitos para el cálculo de estructuras.
La superficie se obtendría simplemente mediante la suma de las áreas de los diferentes triángulos. Puede observarse por lo tanto que no tendería a infinito ya que la superficie queda definida y no aumenta al disminuir el tamaño de los triángulos, sino que se refina.
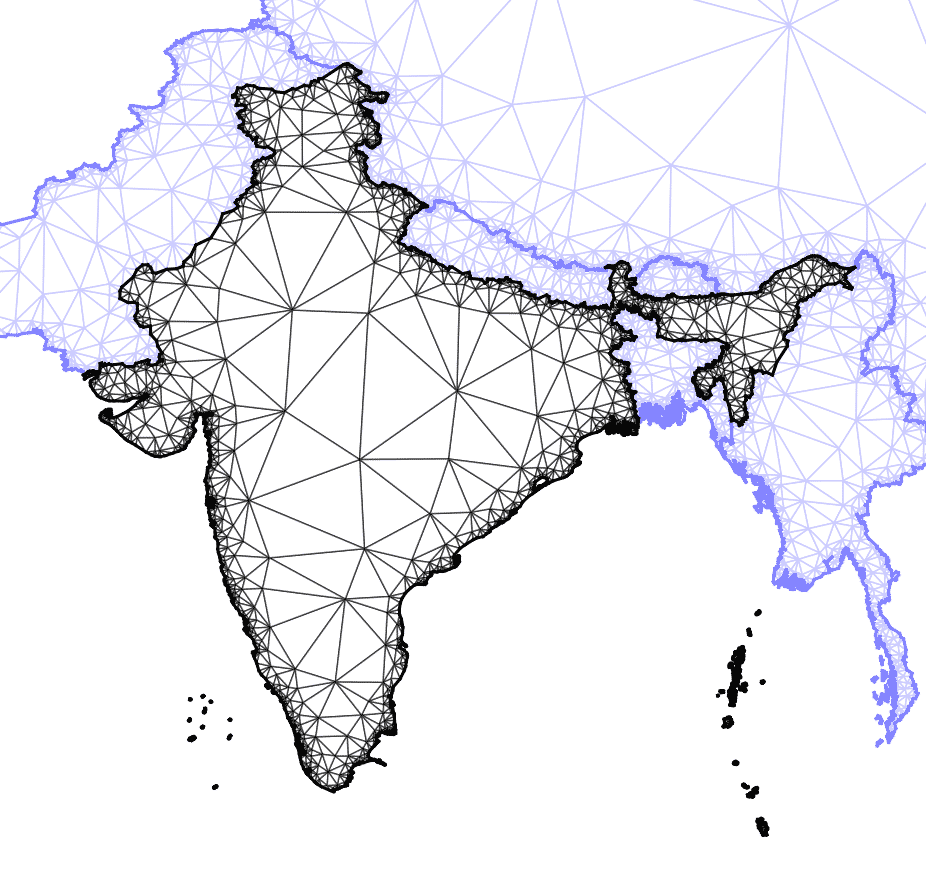
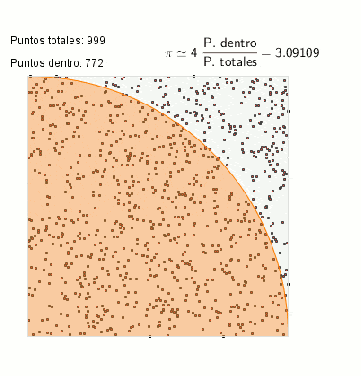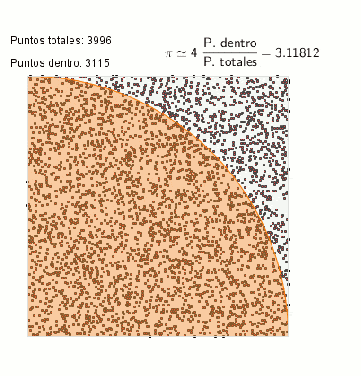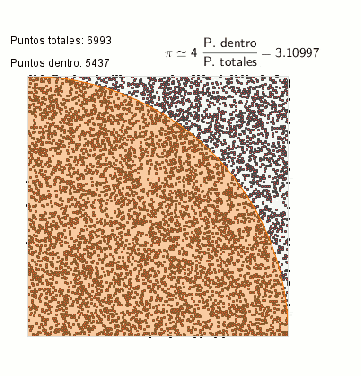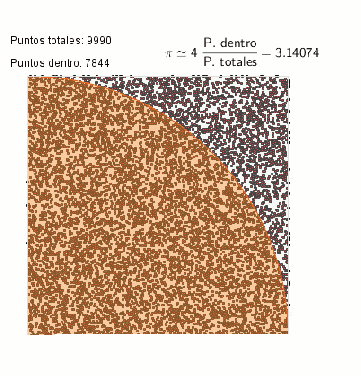
Finalmente, existe una alternativa matemática que permite calcular superficies sin tomar mediciones. Puede calcularse la superficie de un país empleando una generación de Monte Carlo, que no es más que una generación de puntos siguiendo una determinada distribución estadística (generalmente una distribución uniforme). De esta manera, si se generan 1000 puntos en un cuadrado que contiene a un país de forma indeterminada, la relación entre superficie de país/superficie de cuadrado es proporcional al cociente entre el número de puntos dentro/fuera de la región delimitada por el país. Con dicha generación puede aproximarse por ejemplo el valor del número pi por medio del área de una circunferencia.
¿Por qué superficie si pero longitud no?
Llegados a este punto os estaréis preguntando… ¿Cómo puede medirse la superficie si no puede saberse la longitud de costa? ¿No se cometen errores de medición?
La respuesta es que es una paradoja. Y tiene muchísima similitud con la paradoja ya vista de la Trompeta de Gabriel, en la que un cuerpo geométrico podía tener superficie infinita pero volumen finito.
La clave está en la aproximación. En ambos casos se emplea una aproximación para obtener el valor «real». Lo que ocurre es que la variable que se mide pero que a su vez se aproxima es la longitud (m).
Por lo tanto, en el caso de la longitud de costa, uno puede intentar aproximar el perímetro por medio de una especie de interpolación superponiendo una curva suave por encima de la irregular pero al fin y al cabo está despreciando valores infinitesimales \(dx\) entre punto y punto de interpolación. Y un valor infinitesimal es un valor muy muy pequeño en comparación con la variable que estamos midiendo, pero nunca es 0. Dicho valor infinitesimal, repetido por lo tanto entre las miles de aproximaciones que se hacen al interpolar puntos aproximados (como se tiene en cuenta por ejemplo al realizar una integración), generan un valor lo suficientemente grande como para que el error tienda a infinito en fractales y lo sea prácticamente al medir costas irregulares.
En el caso de las superficies, la variable que se aproxima vuelve a ser la longitud (m) (el perímetro), pero lo que estamos midiendo ahora es área o superficie (m^2). Es aquí donde radica la clave; la longitud está al cuadrado. En ese caso, para los que sepan de matemáticas (o, más bien de matemáticas aplicadas a la ingeniería), saben que en una suma que involucre términos \(dx\) y \(dx^{2}\) este último puede despreciarse porque un valor muy pequeño elevado al cuadrado es muchísimo más pequeño que un valor muy pequeño. De hecho, este mismo concepto o aproximación se emplea en la definición de las tensiones de la Teoría de la Elasticidad por poner un ejemplo aplicado a la ingeniería.




¿Y oficialmente de qué tamaño es la regla que se utiliza para medir la longitud de la costa?