Una bomba de aire es una máquina que nos permite aumentar manualmente la presión de un fluido. Cuando esta máquina es accionada por un motor suele llamarse compresor.
Todo el mundo ha usado una alguna vez. Para hinchar balones principalmente, aunque también para hinchar ruedas o colchonetas. Además, solemos diferenciar entre bombas manuales y bombas “eléctricas”, que requieren de energía para funcionar. Y yo os pregunto, ¿Podemos hinchar cualquier cosa con una bomba de mano? ¿Podemos hinchar una pelota con la boca? Una vez leído este artículo sabrás la respuesta y las limitaciones físicas debido a la presión.
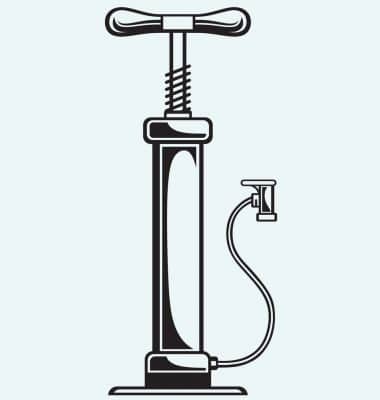
Funcionamiento de una bomba de aire
El mecanismo de una bomba de aire es bastante sencillo pero la mayoría lo desconoce. Llama la atención cómo es capaz de chupar el aire del exterior pero bombearlo justo donde queremos.
Esto se hace por medio de dos válvulas antirretorno.
Una válvula es un dispositivo que permite/impide el paso de un flujo. Haciendo una analogía con la corriente eléctrica, sería como un interruptor.
Una válvula antirretorno o unidireccional es un dispositivo que permite el paso del fluido en una dirección pero bloquea en el caso del sentido contrario. Los diseños de este tipo de válvulas son muy variados, y normalmente involucran una bolita de metal o un resorte.
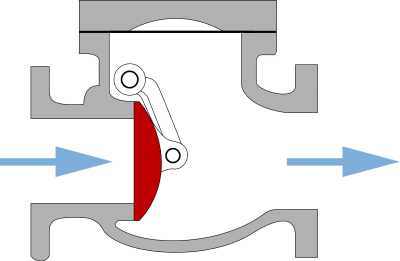
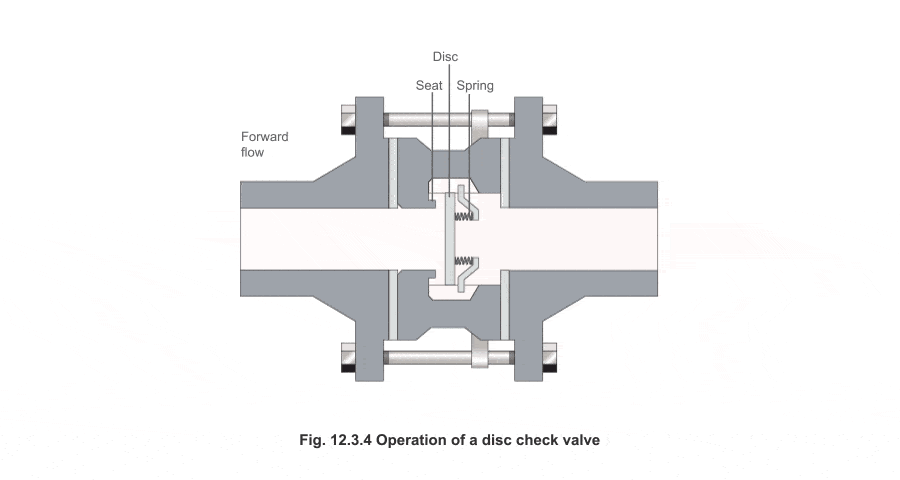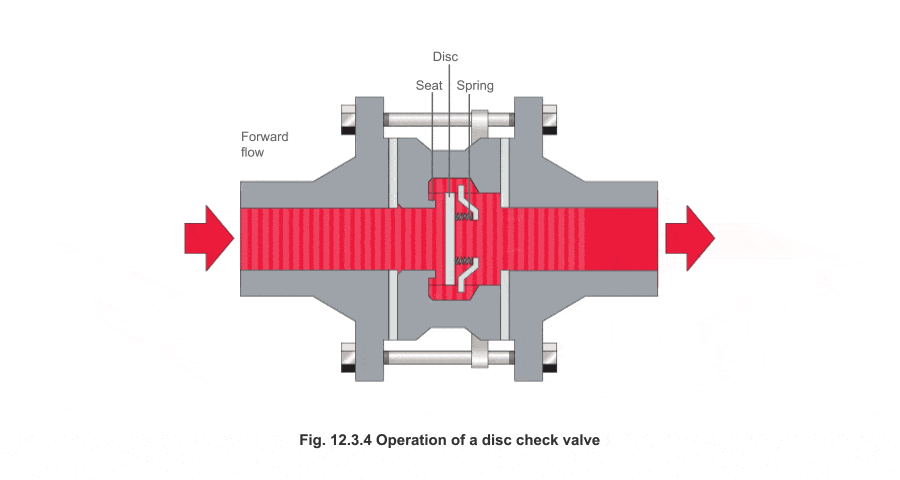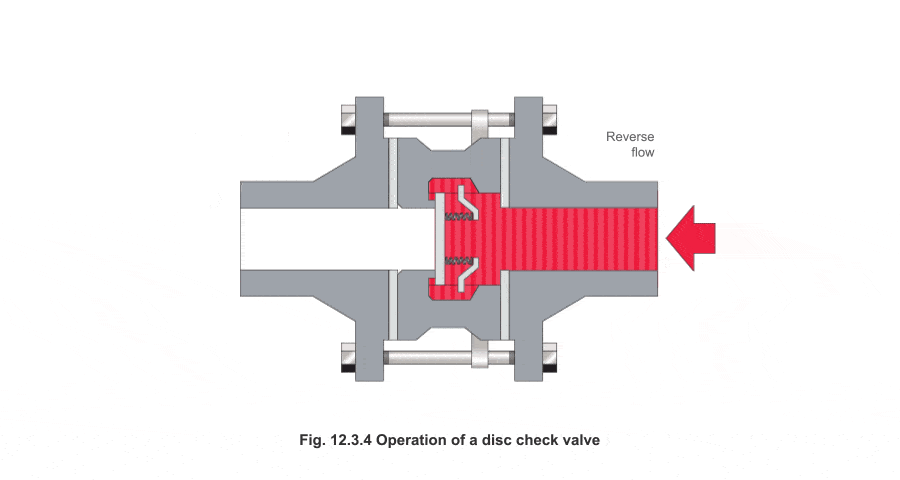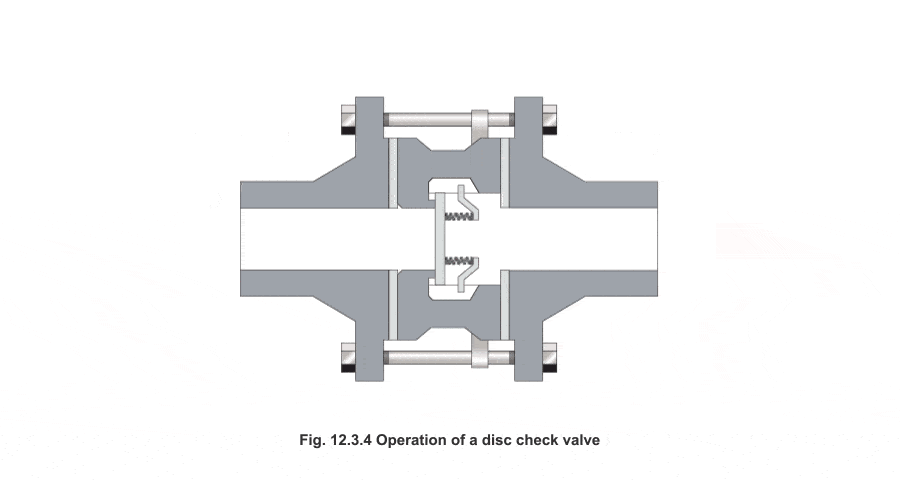
Sin embargo, cuando no existe flujo o es en sentido contrario, el muelle tiende a cerrarla
De esta forma, se colocan dos válvulas antirretorno con sentidos opuestos. Cuando el émbolo sube (Cogemos aire), permitimos que entre aire del exterior exclusivamente. Cuando bajamos el émbolo, la válvula que comunica con el exterior se cierra y se abre la que comunica con lo que queremos inflar.
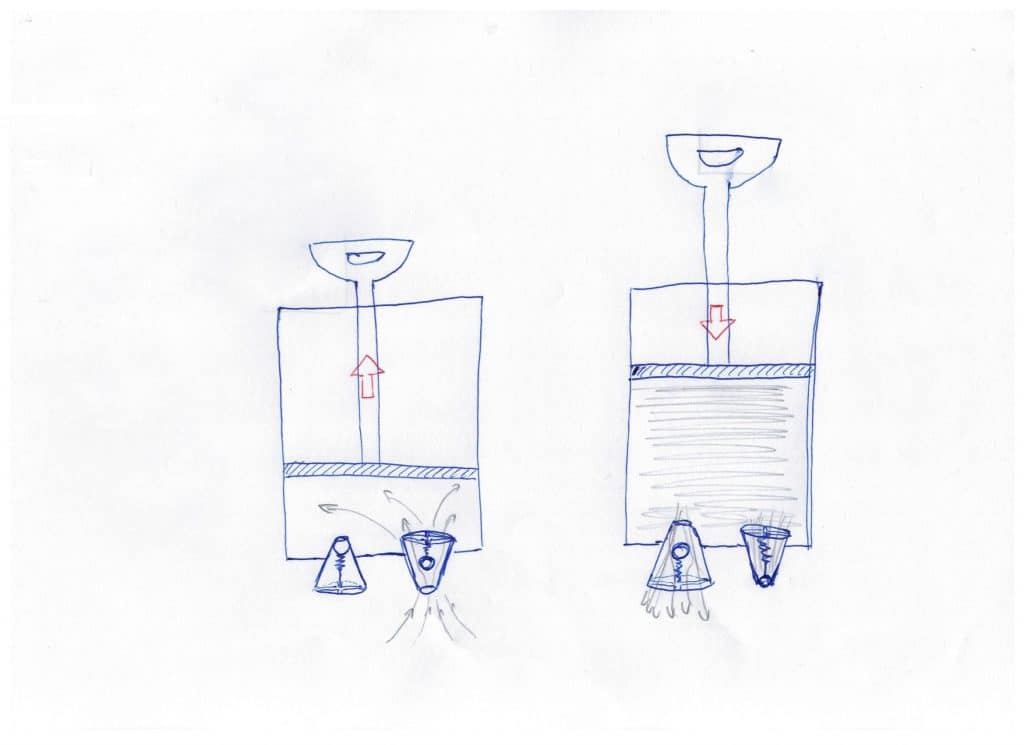
Cuando subimos el émbolo entra el aire y cuando lo bajamos lo expulsamos. Quizás es obvio que cuando bajamos el émbolo empujamos el aire hacia fuera y por eso sale. Pero, ¿Por qué iba el aire a entrar?
Presiones en una bomba de aire
El movimiento del aire viene dado por un gradiente de presiones. Volviendo a hacer analogía con la corriente eléctrica, la presión para un fluido es como el voltaje para la electricidad; Va desde donde hay más a donde hay menos.
Cuando subimos el émbolo, en un primer instante estamos aumentando el volumen de la cámara sin introducir nada de aire. Por lo tanto, las moléculas de aire tienen más espacio para moverse y disminuye la presión. Es aquí cuando el aire del exterior detecta esta disminución de presión y tiende a entrar en nuestra bomba.
Cuando bajamos el émbolo tendemos a comprimir el aire. Al aumentar la presión, el aire encuentra una vía de escape y sale hacia afuera. Pero, ¿Qué ocurre si al otro lado hay más presión que en el interior?
Equilibrio de fuerzas
Vamos a suponer el caso de querer llenar una pelota. Teniendo el émbolo a la máxima altura, la presión en la pelota será de \(P_{p}\), mientras que la presión del aire que se encuentra dentro de la bomba será aproximadamente igual a la presión atmosférica \(P_{a}\).
En cuanto la pelota se llena de aire y sus paredes se estiran, sabemos que \(P_{p} \geq P_{a}\) ya que a la presión atmosférica del exterior se suma la presión que las paredes elásticas ejercen sobre el aire. En este punto podemos decir que, de no aplicar una fuerza, el émbolo no bajará y el aire no tenderá a entrar en la pelota de forma natural.
Lo que necesitaremos entonces para mover el aire de nuestra bomba a la pelota será aumentar la presión en la bomba. Al ejercer una fuerza sobre el émbolo iremos aumentando progresivamente la presión de la cámara hasta que sea igual o mayor a la que se encuentra en la pelota, momento en el que se abrirá la válvula y comenzará a moverse el aire.
Siendo \(P_{b} \ \) la presión dentro de la bomba, haciendo equilibrio de fuerzas en el émbolo podemos calcular la fuerza necesaria para mantener en equilibrio la cámara:
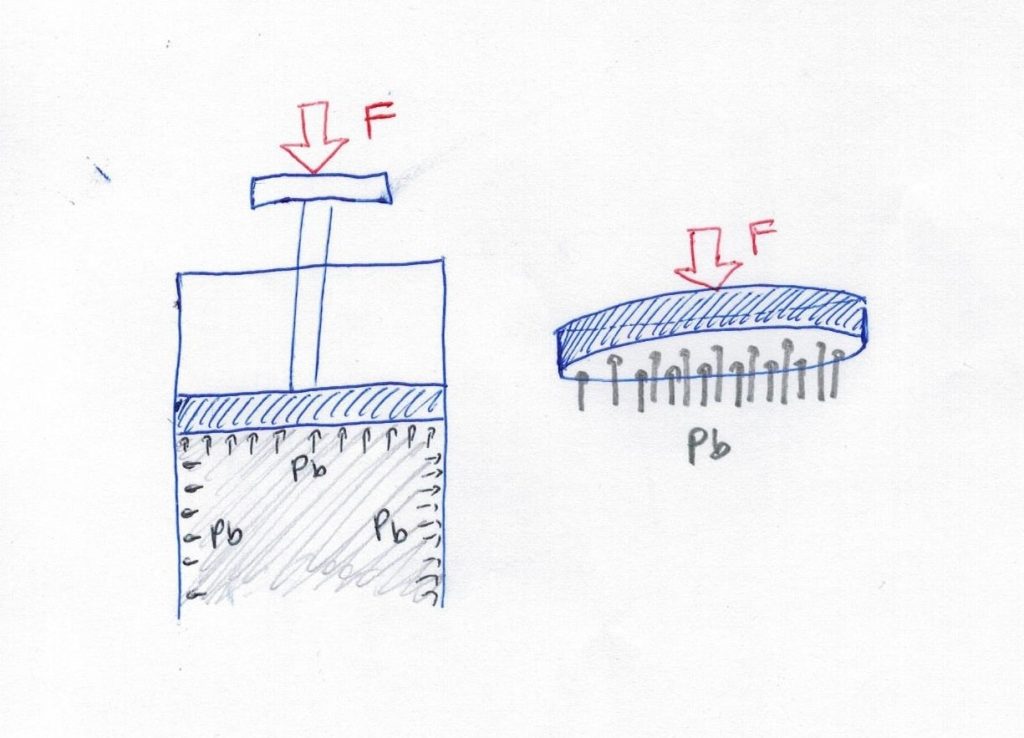
\(\sum \vec{F} = F – P_{b}*A = 0 \iff P_{b}=\frac{F}{A}\)
Como la condición para que la pelota se infle es la de \(P_{b}>P_{p}\), para que exista movimiento de aire debemos de aplicar una fuerza tal que \( \frac{F}{A} \geq P_{p}\)
- De aplicar una fuerza menor a la necesaria, el émbolo bajará debido a la comprimibilidad del aire pero no existirá flujo entre la bomba y la pelota.
- Si la fuerza es mayor a la requerida, la fuerza “extra” se convertirá en aceleración del émbolo, de manera que este se moverá (Descenderá) mientras que el aire va de la bomba a la pelota.
A medida que la pelota se hincha, aumenta la presión en su interior. Por lo tanto, puede que eventualmente nuestra fuerza no sea suficiente para aportar la presión requerida por la pelota. Sin embargo, hemos ignorado el término \(A\) que representa el área del émbolo.
Observamos que, a medida que disminuye el área del émbolo, la fuerza requerida para alcanzar la misma presión es inferior. ¿Supone esto que si tenemos un émbolo de área infinitesimal, podremos aplicar una presión quasi-infinita?
Y como respuesta podríamos decir… Sí… Pero, ¿No?
Bueno bueno, echa el freno. En este blog se respetan las leyes de la Termodinámica, lo juro.
La cosa es que, haciendo las cuentas, una fuerza ejercida sobre un área virtualmente infinitesimal produciría una presión virtualmente infinita. Pero no nos llevemos las manos a la cabeza porque este fenómeno lo observamos todos los días.
Por ejemplo, ¿Por qué creéis que corta un cuchillo? La enorme presión que ejerce la hoja es capaz de superar los esfuerzos que unen a un material y hace que se separe. De no estar afilado, no corta. Lo mismo ocurre si nos pisan la mano con un zapato o con un tacón. El tacón hace “más daño” a pesar de que el peso de la persona es el mismo.
Pero ese no es el tema. A nosotros lo que nos intriga es pensar que, dada la misma fuerza, la presión que generamos es mayor o menor en función del área del émbolo. Entonces, con una bomba de mano... ¿Podríamos levantar un coche?
La respuesta es afirmativa y a alguno les sonará. Y es que este artilugio existe. Se llama gato hidráulico y se basa en el Principio de Pascal.
Y, ¿Cómo se argumenta este aumento de fuerzas desde un punto de vista Termodinámico?
Es cierto que si tenemos una bomba muy muy estrecha, vamos a poder generar presiones mucho más altas y con menos esfuerzo que si tenemos una bomba ancha. Sin embargo, aumentar la presión del aire implica disminuir el volumen existente. Se demuestra que, a menor área, la fuerza requerida es menor. Sin embargo, la distancia que debe de recorrer el émbolo es mayor, y por lo tanto el trabajo realizado es el mismo sea cual sea la bomba.
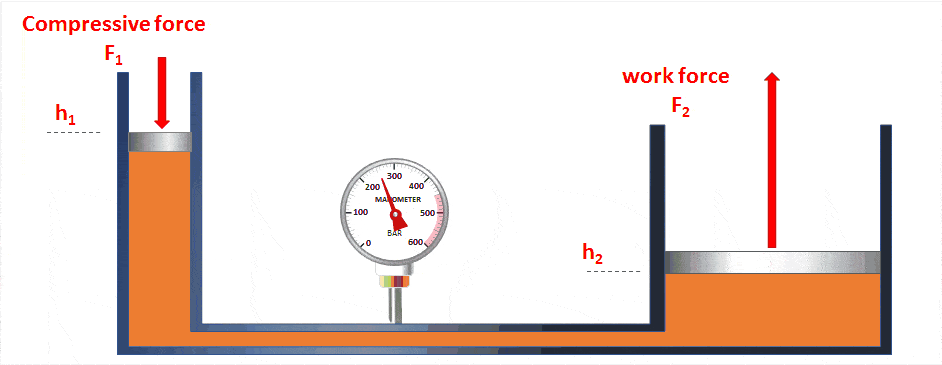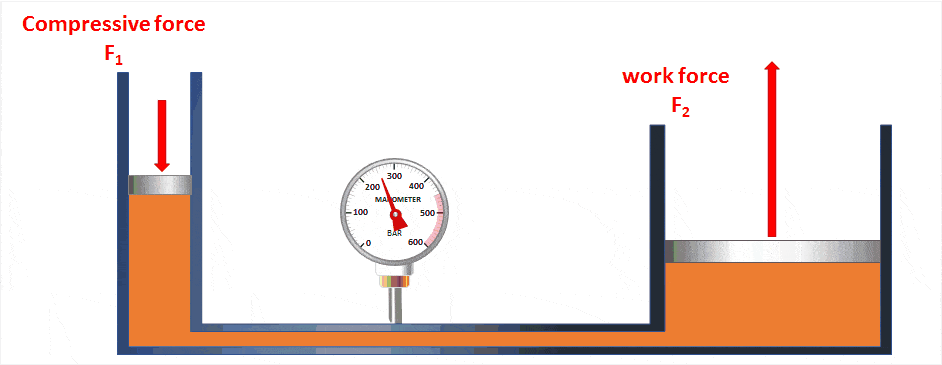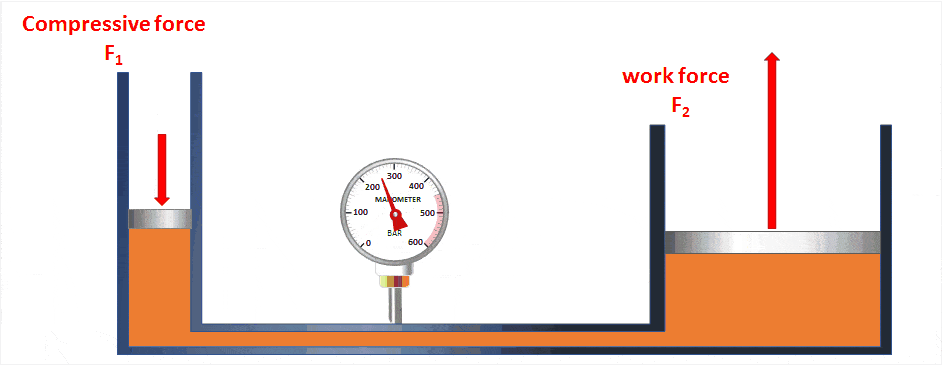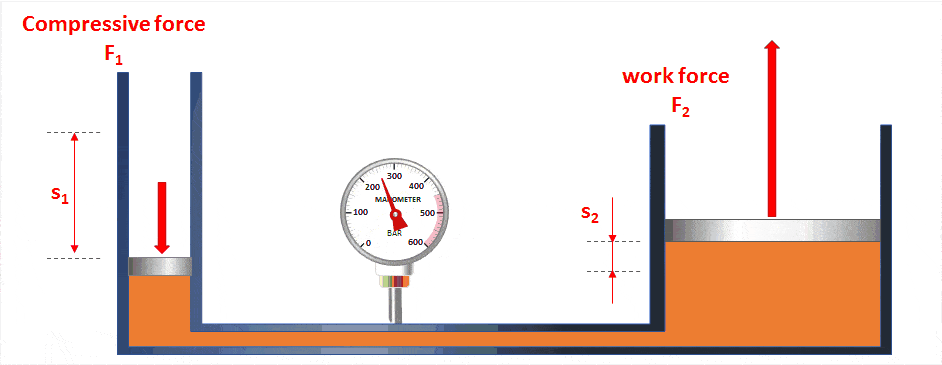
Las poleas, las marchas de la bici, las palancas… en todos estos mecanismos ocurre un fenómeno similar.
Con una bomba estrecha podríamos llenar el neumático de un coche fácilmente pero tardando mucho tiempo, mientras que con una bomba ancha apenas tardaríamos aunque sería necesaria una gran fuerza.
Cuando venden una bomba en algún lado mencionan los psi. Esta presión no es la presión máxima que podemos generar, sino la que es capaz de aguantar las paredes de la bomba sin que explote. Por supuesto excede enormemente a la que podríamos generar/hinchar y, por lo tanto, este dato no es muy útil a la hora de elegir una bomba.
¿Podemos llenar una pelota con la boca?
Cuando inspiramos y espiramos, nuestros pulmones actúan como una bomba. El émbolo en este caso es nuestro diafragma, y las paredes de la bomba son los pulmones.
Cada persona, dada su edad y musculatura, tendrá una fuerza máxima que es capaz de desarrollar por el diafragma. El límite lo marca o nuestra musculatura o los pulmones.
Al ser el tamaño de nuestro diafragma fijo y estar nuestra fuerza acotada, la presión máxima que podremos ser capaces de generar se encontará limitada. Se estima que la presión máxima que un trompetista profesional puede generar es de 1.9 psi o 13kPa.
Y ya no sólo es la presión que podemos generar. Es la presión que nuestros pulmones pueden resistir sin romperse. Se estima que la presión máxima que aguanta un pulmón promedio es de unos 2.8 psi o 19.3 kPa. Es por ello que es importante el efecto de la presión en el cuerpo humano, especialmente en el caso de los apneístas.
Tranquilos, no tengáis miedo de dañaros los pulmones por soplar fuerte ya que como hemos visto el límite se encuentra mucho más alejado de la presión que somos capaces de generar por nuestra cuenta.
La 2ª regla del fútbol establece que la pelota debe de tener una presión comprendida entre 8.7 y 16.1 psi (60 – 111 kPa) sobre el nivel del mar. Por lo tanto, excede enormemente a la presión que somos capaces de generar con nuestros pulmones. Al intentar llenarlo desde vacío podríamos inflarlo un poco, pero rápidamente llegaríamos al tope en cuanto se estirasen las paredes. Llegados a este punto soplaríamos al máximo pero no seríamos capaces de abrir la válvula.
Presión respecto al nivel del mar
Durante todo el artículo hemos estado hablando de presiones. Y es que, hemos dicho por ejemplo que un pulmón soporta un máximo de 2.8 psi. Sin embargo, nosotros nos encontramos sumergidos en un fluido: El aire. Eso hace que, al nivel del mar, la presión absoluta que sufren TODOS los objetos es de 1 atmósfera o 14.7 psi.
¿Qué sucede entonces?
Cuando la presión se mide en relación a un vacío perfecto (En el espacio por ejemplo) se denomina presión absoluta. Cuando se mide con respecto a la presión atmosférica, se llama presión manométrica.
La presión que mide un manómetro es la presión manométrica. Es decir, cuando el sistema a analizar se encuentra a presión atmosférica la aguja marca un 0, ya que no hay una diferencia de presión entre el sistema analizado y el entorno atmosférico. Por lo tanto, siempre que hablamos de presiones nos referimos al incremento de presión respecto a la presión atmosférica.

Las presiones por debajo de la atmosférica reciben el nombre de presiones de vacío y se miden con medidores de vacío (o vacuómetros), que indican la diferencia entre la presión atmosférica y la presión absoluta.
Al igual que establecemos de forma arbitraria la escala de temperaturas (El 0º lo marca la solidificación del agua), la escala de presiones también se establece en base a una presión de referencia: La presión atmosférica.
Sin embargo, no perdamos de vista la escala absoluta. Esta escala relativa se usa para situaciones en los que es más cómodo colocar simplemente un 0 para ahorrarnos números. Cuando resolvemos un problema en ingeniería, al igual que con la temperatura (¡Siempre en Kelvin!) la presión siempre se expresa en una escala absoluta (Y en Pascales).




![Avtomat Kalashnikova modelo 1947 [AK-47]: El arma perfecta Portada de AK-47](https://ingenieriabasica.es/wp-content/uploads/2020/04/Portada-AK-47-200x103.jpg)
mola
Muy bien explicado, cuando se conoce el tema se puede explicar en forma sencilla. Lo felicito
Muchas gracias Raúl
Un saludo
Me gusta muy explicado y se encuentra fácil de entender
Gracias
Tengo una bomba de pie y no podía hacerla funcionar, y me dije voy a investigar, y oí que, los que nacimos antes de los 90 no podíamos usarla y nos explicarían porque? ahora el pivote se usa al revés.. tire una bomba de pie y compré otra y lo mismo, jajaja, y está excelente platica sobre la Física de las presiones, ya me explica mejor su funcionamiento, muchas gracias.
jajajajja interesante historia, gracias por tu respuesta Jorge!!!