¿Hay gravedad en la ISS? ¿Por qué flotan los astronautas?

Al pensar en la Estación Espacial Internacional (International Space Station ISS) nos imaginamos a los astronautas flotando. Pensamos que están tan lejos de la tierra que no les afecta el campo gravitatorio y por eso flotan.

En este artículo vamos a ver si es verdad que en la ISS no hay gravedad, y daremos una explicación a por qué flotan.

Estimación de la gravedad en la ISS

Vamos a estimar la intensidad del campo gravitatorio y el peso de la ISS a esa altura para ver si la gravedad es nula. Sabemos que la fuerza gravitatoria sigue la siguiente fórmula:

\(\boxed{ \|F\|=G{\frac {m_{1}*m_{2}}{r^{2}}}}\)

Es decir, proporcional a las masas e inversamente proporcional al cuadrado de la distancia.

Para poder calcular la fuerza de atracción que actúa sobre la ISS partiremos de los siguientes datos:

• Masa de la Tierra: 5,972 × 10^24 kg
• Masa de la ISS: 419.455 kg
• Constante Gravitación Universal: 6,674 × 10^-11 [N*m^2*kg^-2]
• Radio medio de órbita: {6,371 * 10^6 + 400.000} m

Introduciendo todos estos números en la fórmula obtenemos:

\(\|F\| = 6,674*10^{-11} *\frac{5,972 * 10^{24} *419455 }{6.771.000^{2}} = 3,6466 * 10^{6} \ N\)

Que representa el peso de la ISS en el campo gravitatorio de la Tierra a esa distancia. Si queremos calcular la intensidad del campo gravitatorio, sólo tenemos que dividir entre la masa de la ISS:

\(\|F\| = m*g’ \rightarrow g’ = \frac{\|F\|}{m}=\frac{3,6466 * 10^{6}}{419455} \approx \boxed{8,693 \ m/s^{2}} \ ? \ ? \ ?\)

¿¿¿8,693 m/s^2??? Es un valor que, respecto a los 9,81 m/s^2 presentes en la superficie terrestre, no difiere demasiado. Y más teniendo en cuenta que en la Luna por ejemplo la intensidad es de 1,625 m/s^2 y aún así los astronautas sienten la gravedad. Es decir, que en la ISS SÍ hay gravedad.

Entonces, llegados a este punto nos preguntamos… Si en la ISS la gravedad afecta casi del mismo modo que en la superficie, ¿Por qué flotan los astronautas?

Ingravidez

Ni gravedad 0, ni anti-gravedad ni gravedad nula. Lo que se produce en la ISS es un estado de ingravidez, que se define como el estado en el que un cuerpo que tiene un cierto peso se contrarresta totalmente con otra fuerza o se mantiene en caída libre sin sentir los efectos de la fuerza gravitatoria.

De hecho, en ningún punto de la galaxia existe una ausencia de gravedad, porque por muy pequeña que sea, siempre es existente. Por ejemplo, la fuerza de gravedad que ejerce la Luna. En su superficie es débil y en la Tierra es muchísimo más débil aún, pero sin embargo su papel es fundamental en las mareas.

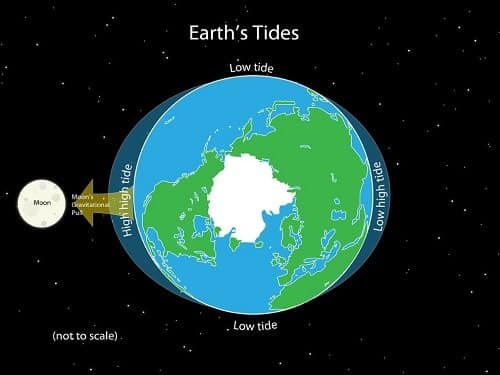
El campo gravitatorio es una fuerza por unidad de masa (Fuerza distribuida), y por lo tanto la única forma de anularla es empleando otra fuerza distribuida que tenga igual valor pero sentido opuesto. Mecánicamente, y de una manera similar a la aceleración del campo gravitatorio, aparecen las fuerzas de inercia.

La aceleración de un cuerpo no es más que la fuerza de inercia que sufre un cuerpo por unidad de masa distribuida, al igual que ocurre con el campo gravitatorio y el peso. Es una fuerza que aparece únicamente cuando un cuerpo sufre una aceleración, y actúa con sentido opuesto a esta.

Es complicado establecer un valor y dirección de las fuerzas de inercia ya que dependen del movimiento del cuerpo y las fuerzas que actúan sobre él. Empleando una formulación de las fuerzas según el Principio de D’Alembert, obtenemos el resultado de que en todo momento las suma de las fuerzas activas y de inercia debe de ser nula. De esta forma obtenemos su valor indirectamente;

\(\sum_{i=1}^{n} \vec{F}_{i} + \vec{F}_{in} = \vec{0} \rightarrow \boxed{\vec{F}_{in} = -\sum_{i=1}^{n} \vec{F}_{i}}\)

Cuando sobre un cuerpo sólo actúa la fuerza de la gravedad, las fuerzas de inercia son de igual valor y sentido opuesto a esta, y por lo tanto se anula completamente. De esta forma, se establece el estado de ingravidez, donde las cosas no pesan.

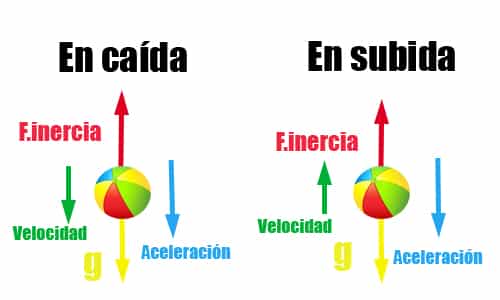
En un cuerpo en caída libre, la gravedad tira hacia abajo. Sin embargo, la inercia le tira hacia arriba, como cuando estamos en un coche acelerando. Esto es lo que produce que se anule el peso.

Además, no es necesario ni que esté cayendo hacia abajo, sino que un cuerpo lanzado hacia arriba también lo experimenta. Un cuerpo lanzado hacia arriba sufre la gravedad hacia abajo y una deceleración o aceleración negativa que genera una fuerza de inercia hacia arriba, como cuando un coche frena. De esta forma, también se anula la gravedad.

En microgravedad, los líquidos tienen a agruparse en forma de esferas. Esto se debe al concepto de tensión superficial ya que la esfera es el cuerpo tridimensional con mayor volumen y menor superficie.

El caso de la ISS es un caso un tanto particular. La ISS se encuentra en caída libre, es decir, es como si estuviese cayendo constantemente. Sin embargo, la caída en vez de ser en dirección hacia la Tierra es proyectada tangencialmente en forma de órbita. De este modo, la inercia en forma de aceleración centrífuga anula la fuerza de la gravedad, manteniendo la órbita y la caída de forma casi ilimitada.

Si en una nave espacial se encienden los propulsores, la microgravedad desaparece y los tripulantes se sentirían atraídos hacia la parte trasera de la nave debido a la inercia.

Cuerpo en movimiento acelerado

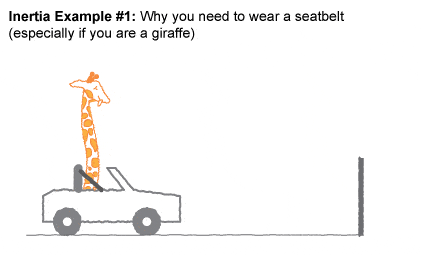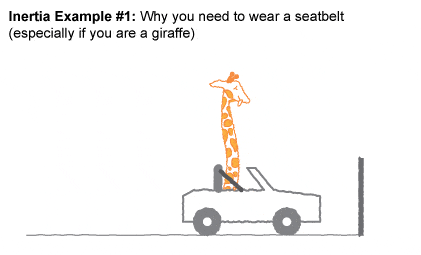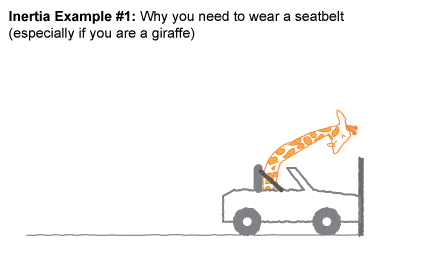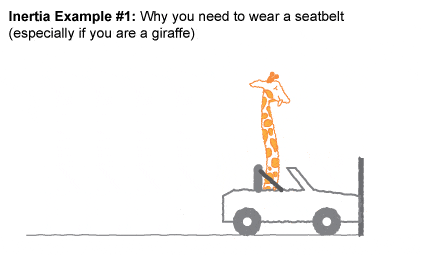
Cuando un cuerpo se encuentra en movimiento acelerado, entran en juego las fuerzas de inercia. Estas, según el Principio de D’Alembert, actúan de forma opuesta a la aceleración. Para que comprendamos mejor este concepto vamos a analizar el comportamiento de un coche.

Con el coche parado, sentimos únicamente la fuerza de la gravedad. A medida que comenzamos a acelerar hacia delante, nuestro cuerpo sufre una fuerza de inercia hacia atrás. Sin embargo, hay un obstáculo: el respaldo. El respaldo ejerce una fuerza de reacción sobre nuestra espalda igual a la fuerza de inercia, y al igual que en el caso de la gravedad con el asiento, se genera una compresión. De esta forma, sentimos como que nos «pegamos» al asiento.

Cuando el coche alcanza una velocidad constante, esta sensación de estar pegados al asiento desaparece, y sólo notamos la reacción del asiento hacia arriba (Peso). Un coche podría ir a 450 km/h estables y no sentiríamos absolutamente nada sobre nuestras espaldas, ya que inercialmente estar en reposo o en velocidad constante es lo mismo (Ausencia de fuerzas). Es lo que sucede básicamente cuando vamos en un AVE o un avión en velocidad de crucero.

Si sobre un cuerpo no actúa ninguna fuerza, este permanecerá en movimiento rectilíneo uniforme (o en reposo) indefinidamente

Primera Ley de Newton

De hecho, es lo que sucede actualmente con nosotros en la Tierra. La Tierra rota a unos 465 m/s (1.674 km/h) en el ecuador, gira alrededor del Sol a unos 29,8 km/s (107.280 km/h) y se mueve a la par que el Sol a lo largo de la galaxia a unos 220 km/s (792.000 km/h). Sin embargo, no salimos volando ni nos sucede nada extraño ya que todas estas velocidades suceden sin apenas aceleraciones.

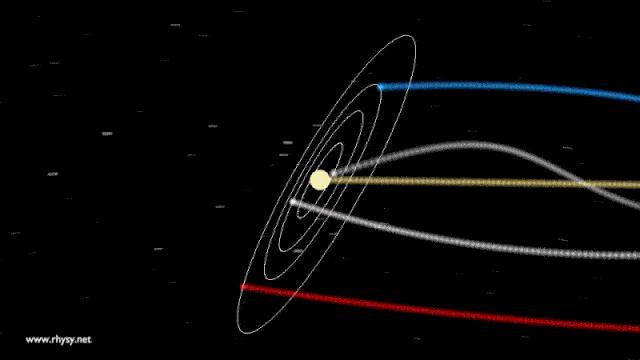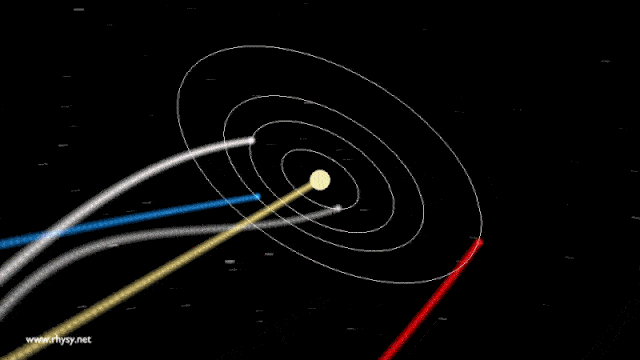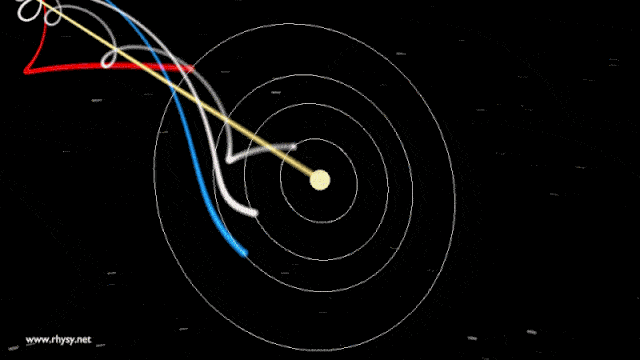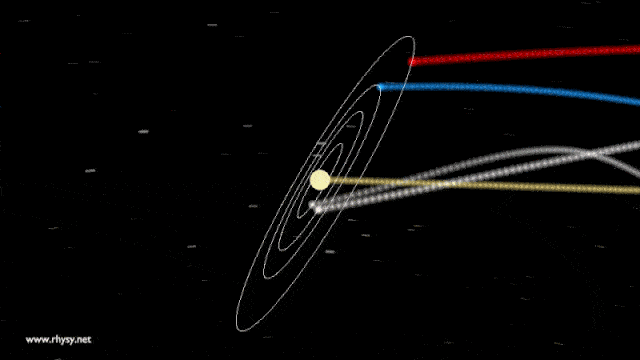
La respuesta a la típica pregunta de ¿Qué pasaría si la Tierra de repente dejase de rotar? es obvia: saldríamos volando como en un accidente de coche a 1.674 km/h y moriríamos al instante.

Simular ingravidez en la Tierra

Hemos dicho que con lanzar un cuerpo en caída libre el peso se anula. Y esto es verdad. Si saltásemos desde un rascacielos, durante la caída sentiríamos lo mismo que sienten los astronautas de la ISS, aunque con un pequeño detalle.

En el entorno de la ISS apenas hay atmósfera, por lo que el rozamiento con el aire es casi despreciable y el entorno no es de total ingravidez pero casi. Sin embargo, en nuestro caso, si saltásemos desde un rascacielos únicamente estaríamos en ingravidez un par de segundos. Una vez alcanzásemos una velocidad elevada el aire haría de las suyas y comenzaríamos a sentirnos presionados. De hecho, es lo que le ocurre a los paracaidistas con la velocidad terminal. No obstante, podéis hacer la prueba en casa saltando y comprobar la ingravidez durante un par de segundos.

Ingravidez ≠ Fuerza ilimitada

Cuando pensamos en la ingravidez, pensamos estar en un entorno donde nada pesa y todo se mueve sin dificultad.

A pesar de no haber gravedad, los cuerpos siguen teniendo masa, y para ponerlos en movimiento hace falta ejercer una fuerza. Si bien no os creéis la historia de la conservación de la cantidad de movimiento o la 2/3ª Ley de Newton, es fácil de entender que si el movimiento implica una acumulación de energía cinética, esta energía debe de ser aportada de algún modo.

Imaginemos que estamos en ingravidez y queremos mover un coche. Podríamos levantar el coche, colocarlo sobre nuestra cabeza y sostenerlo con un meñique sin problemas ni necesidad de hacer fuerza. Sin embargo, si quisiésemos darle un empujón y lanzarlo lejos, ahí tendríamos que realizar fuerza para poder ponerlo en movimiento. Además, al inicio para levantarlo tendríamos que hacer fuerza para inducir el movimiento, y al colocarlo sobre nuestra cabeza tendríamos que volver a hacer fuerza para frenarlo.

Sin embargo, el hecho de que no pese puede comprobarse fácilmente desde casa saltando. Coged algo que pese (Una silla, una pesa, un ventilador) y saltad. El salto costará más trabajo en las piernas porque el peso es mayor, pero una vez en el aire los brazos se sentirán libres durante el salto.

Simular ingravidez tiempo prolongado. Vuelo parabólico

Lo malo de dar un salto es que la ingravidez dura apenas 1 segundo. Lo malo de saltar de un rascacielos es que morimos al caer. Habrá un punto intermedio, ¿No? Pues para eso inventaron el vuelo parabólico.

Un vuelo parabólico es un vuelo en el que un avión preparado (Cabina vacía y acolchada) es elevado para luego dejarlo en caída libre y así simular un entorno de microgravedad.

Se llama vuelo parabólico porque el avión describe parábolas, alternando tramos de microgravedad (Caída libre) con tramos de sobregravedad (Al ascender). De esta manera, de forma controlada pueden obtenerse períodos largos de microgravedad sin sufrir ningún riesgo. Es usado por los astronautas para ser entrenados y por empresas privadas como ZERO-G que venden una experiencia única.

Un experimento curioso en microgravedad es el de dejar caer gatos. Todos sabemos que estos siempre caen de pie. Pero… ¿Y en el espacio? Comprúebalo con el siguiente vídeo:

EXTRA: La ISS: Fuerzas, velocidades y cómo verla desde la Tierra

Tras introducir los conceptos y poner un par de ejemplos vamos a centrarnos en la ISS. ¿Qué fuerzas de inercia sufre? ¿A qué velocidad orbita y por qué? ¿Podemos verla desde la Tierra?

Antes de nada, hay que saber por qué la ISS se encuentra orbitando a esa altura determinada.

• Una altitud excesiva (Superior a los 500 km) supondría una exposición elevadísima a la radiación, siendo muy perjudicial para la tripulación y la electrónica de la nave. Además, a mayor altura, la dificultad para llegar a la estación aumentaría y mayor combustible sería necesario.
• Una altitud muy baja supondría una mayor interacción con la atmósfera y por lo tanto pérdidas debido al rozamiento. Además, la ISS se encuentra en ingravidez intencionadamente para poder hacer experimentos, y con la acción del rozamiento desaparecería esta ingravidez. Se estima que como mínimo se requieren 280 km para no sufrir demasiado el rozamiento con la atmósfera.

Teniendo en cuenta estos puntos, se decidió colocar la ISS a una altitud alrededor de los 400 km. Que, respecto a las órbitas de la mayoría de los satélites, es bastante baja.

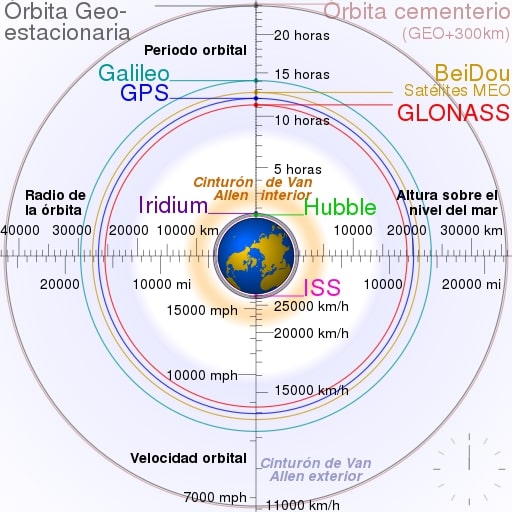
Una vez conocida la altitud, para calcular algunos valores tenemos que hacer un análisis de las fuerzas principales* que actúan sobre ella: La gravedad y la fuerza centrífuga (Inercia).

*A esa altitud sigue existiendo un rozamiento mínimo con la atmósfera que, si bien día a día es pequeño, tras semanas la acción es importante. Por ello la ISS cuenta con propulsores que la aceleran de vez en cuando para recuperar la órbita nominal.

La aceleración de la gravedad a esa altura ya la hemos calculado, y es de 8,963 m/s^2. Para que ambas fuerzas se encuentren en equilibrio la aceleración centrífuga debe de ser de igual magnitud.

• Una aceleración centrífuga mayor supondría que la ISS se alejase de la Tierra
• Una aceleración centrífuga menor supondría que la ISS cayese a la Tierra

La fórmula de la aceleración centrífuga (Caso particular de inercia) es \(\boxed{a=\frac{v^{2}}{R}}\)

Siendo el radio R conocido (400.000 + 6,371 * 10^6 m) y la aceleración fijada por el valor de la gravedad, nos queda calcular la velocidad a la que la ISS rota:

\(v=\sqrt{a*R} = \sqrt{8,963*(400.000 + 6,371 * 10^6)} \approx 7.660 =7,66 \ km/s\)

Es decir, que la ISS en 24h da 15,56 revoluciones alrededor de la Tierra. Impresionante, ¿No?

Lo bueno de que pase tantas veces alrededor de la Tierra es que se expone a nuestra vista a menudo. Por la noche, si la ISS pasa por encima de nuestra ubicación y la luz del Sol le da directamente, sus grandes paneles solares la reflejan (Como si de la Luna se tratase) y desde la Tierra puede verse con nuestros propios ojos sin problemas. Bajo mi propia experiencia, se ve como si un punto luminoso tipo estrella polar atravesase el cielo a una velocidad moderada, durante 15-20 segundos.

¿No te lo crees? En esta página puedes ver, en base a tu ubicación, cuándo podrás ver la ISS u otros satélites en los próximos días. En mi opinión el resto de satélites son casi imposibles de ver debido a la contaminación lumínica, pero la ISS se ve claramente desde la ciudad.

https://james.darpinian.com/satellites/