El Rey de un pequeño país invita a 1000 senadores a cenar a su fiesta anual. Como es tradición, cada senador lleva al Rey una botella de vino, y estas botellas son servidas en la cena del día siguiente.
Durante la recepción de los asistentes, la Reina se entera de que uno de los senadores intenta asesinar al resto de invitados entregando una botella de vino envenenada. Por desgracia, no saben qué senador, ni qué botella de vino está envenenada, y el veneno es completamente indiscernible.
Sin embargo, el Rey tiene 10 prisioneros que planea ejecutar, y decide utilizarlos como catadores para determinar qué botella de vino contiene el veneno. El veneno, una vez ingerido, no tiene ningún efecto en el prisionero hasta que este muere repentinamente. Además, no se sabe cuándo ocurrirá la muerte, lo que se sabe es que máximo tarda 24 horas en hacer efecto.
El Rey necesita determinar qué botella de vino está envenenada antes de la próxima cena para que las fiestas puedan continuar según lo previsto. Por lo tanto, sólo tiene tiempo para una ronda de pruebas. ¿Cómo puede el rey administrar el vino a los prisioneros para asegurarse de que tras la ronda de pruebas habrá encontrado la botella envenenada?
Análisis del problema de las mil botellas
El problema en sí está bastante claro y el enunciado no tiene informaciones ocultas ni trata de intentar jugar con el azar de la probabilidad de muerte ni nada. Tienes 1000 botellas y 10 prisioneros. Abres la celda, asignas las botellas, la cierras, y tras 24h vuelves a abrir la celda para ver quién ha muerto. El problema es cómo asignar las botellas a los prisioneros para asegurarte de que sabrás inequívocamente cuál de ellas es la que está envenenada.
Solución al problema simplificado: 4 botellas y 2 presos
Solamente una mente muy brillante sería capaz de resolver el acertijo original. No obstante, si se simplifica el problema la solución parece inmediata.
Supongamos que el problema se reduce a sólo 4 botellas y 2 prisioneros. ¿Cómo distribuirías las botellas entre los prisioneros? En este caso es muy sencillo:
- La botella 1 va al prisionero A
- La botella 2 va al prisionero B
- Ambos prisioneros beben de la botella 3
- Ningún prisionero bebe de la botella 4
De esta forma, los posibles resultados tras el experimento serían:
- Si ningún prisionero muere -> La botella 4 era la envenenada
- Si el prisionero A muere -> La botella 1 era la envenenada
- Si el prisionero B muere -> La botella 2 era la envenenada
- Si tanto el prisionero A como el B mueren -> La botella 3 era la envenenada
Esta asignación puede representarse de forma matricial de la siguiente forma:
\(\begin{array}{c|cc} & A & B \\ \hline 1 & 0 & 0 \\ 2 & 0 & 1 \\ 3 & 1 & 0 \\ 4 & 1 & 1 \\ \end{array}\)
Se ha cambiado el orden con respecto al listado original pero está claro lo que se ha hecho. Usando una representación binaria en la que «1» indica que se bebe y «0» indica que no, es posible codificar cada una de las combinaciones de manera única para que pueda saberse qué botella es la envenenada. Por lo tanto, n prisioneros son capaces de generar \(2^{n}\) combinaciones diferentes. En este caso, 2 prisioneros han podido generar 4 combinaciones, suficientes para resolver el problema con 4 botellas.
Solución al problema general del rey y las 1000 botellas de vino
Tras resolver el problema reducido, la solución al problema general es instantánea. Al haber 10 prisioneros, el número de combinaciones únicas asciende a \(2^{10} = 1024\), es decir, que son suficientes para cubrir las 1000 botellas.
Sería entonces muy sencillo. En la etiqueta de cada botella se escribiría un número que la identifica así como su traducción a binario, es decir:
- 1 = 0000000001
- 2 = 0000000010
- 3 = 0000000011
- …
- 45 = 0000101101
- 46 = 0000101110
- …
- 999 = 1111100111
- 1000 = 1111101000
Luego a cada preso se le asigna una posición dentro del número. Por ejemplo, al preso A se le asigna el primer dígito, al preso B el segundo dígito … y al preso J el último dígito. Cada preso va mirando las botellas, y en aquella en la que en su dígito aparezca un 1, bebe. Si en su dígito aparece un 0, la ignora. Así todos los presos con todas las botellas. De esta manera se garantizarían combinaciones únicas que permitirían saber cuál era la botella envenenada. Al día siguiente bastaría con generar un código binario en función de los presos fallecidos y así se podría identificar la botella. Si, por ejemplo, los presos fallecidos fueron B, G, H y J, la botella envenenada sería la 0100001101, es decir, la 269.
La siguiente foto muestra, en el eje X, cada preso, y en el eje Y lo que sería cada una de las botellas etiquetadas. El color negro indica que dicho preso bebe de dicha botella, y el color blanco es que no.
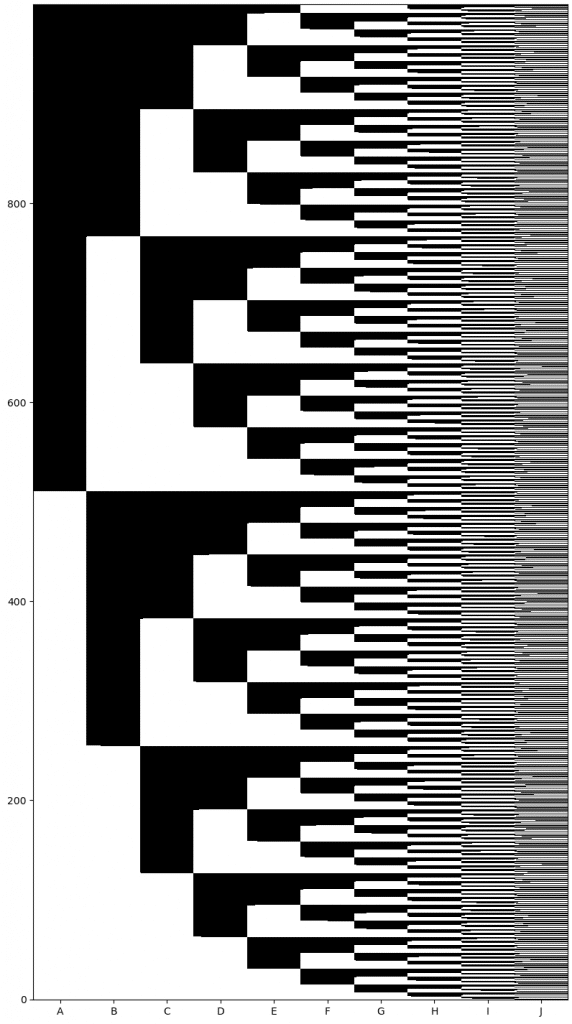
Esta imagen es realmente bella. Por una parte, se ve que cada preso bebe aproximadamente del mismo número de botellas y de manera organizada. Por ejemplo:
- Preso J: Bebe alternando (\(2^{0}\)) 1 botella: {1},{3},{5}…
- Preso I: Bebe alternando (\(2^{1}\)) 2 botellas: {2,3},{6,7},{10,11}…
- Preso H: Bebe alternando (\(2^{2}\)) 4 botellas: {4,5,6,7},{12,13,14,15},{20,21,22,23}…
- …
- Preso A: Bebe alternando (\(2^{9}\)) 512 botellas: {513,514,515 … 999,1000}
Y por otra parte, la imagen en sí parece un fractal y recuerda a un código de barras. Esto no es sorprendente puesto que la representación de los números de barras o códigos QR no es más que pintar en blanco y negro una matriz binaria, lo mismo que se ha hecho en este caso.
¿Qué te ha parecido el acertijo? Lo que faltaría por resolver es cómo hacer que una persona se beba casi 500 copas de vino de una sentada… Los matemáticos no tienen una respuesta para ello (al menos por ahora). ¡Si quieres más acertijos como este no dudes en visitar la categoría de Juegos y acertijos matemáticos! Especialmente el artículo de Los 7 Acertijos Matemáticos, que todavía quedan algunos sin resolver.
