El Efecto Magnus: El mágico gol de Roberto Carlos

Todos recordamos el mitiquísimo gol de falta de Roberto Carlos. Un poco de efecto al tiro, y la pelota realiza un vuelo que deja a cuadros a la defensa y portero incluido. ¿Cuál es la explicación a ese comportamiento? -> El Efecto Magnus.

En este artículo comprenderás por qué se producen los tiros con efecto y un par de aplicaciones importantísimas del efecto Magnus que no conocías.

El Efecto Magnus

Vamos al grano… ¿Por qué se produce el efecto Magnus?

Para que se produzca es esencial una cosa: que el cuerpo se encuentre girando con eje de rotación perpendicular al plano de movimiento. Es decir, que en un dardo girando o en la bala de una pistola no se da el Efecto Magnus a menos que haya una corriente lateral. Esto se debe, como veremos al final del artículo, a la intersección entre corriente y torbellino.

Una vez aclarado esto, vamos a analizar por qué la rotación hace que se desvíe la trayectoria. Y una rápida explicación puede ser dada mediante la ecuación de Bernoulli.

\( \frac{1}{2} \rho \| \vec{u} \|^{2} + P+\rho g z = P_{o} = cte\)

Supongamos que una pelota se mueve tal y como muestra la siguiente animación

Es decir, la pelota avanza y a la vez gira. Partiendo de una corriente que, fijando la pelota como punto fijo, se mueve hacia ella con la velocidad de avance de la pelota, una vez que la alcanza se divide en dos ramas.

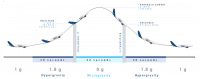
• En una de ellas, la velocidad del viento es a favor de la rotación, sumándose ambos movimientos y produciendo una zona de mayor velocidad. Empleando la ecuación de Bernoulli, si aumenta la velocidad (A misma altitud) debe de disminuir la presión.
• En la otra zona, la velocidad del viento va en contra de la rotación. Sumando ambos efectos, la velocidad que pasa por esta zona es inferior a la velocidad incidente, generándose una zona de alta presión, ya que siguiendo el mismo planteamiento al disminuir la velocidad aumenta la presión.

Una vez descrita la distribución de presiones alrededor del cuerpo, basta con integrarla sobre la superficie de la pelota y obtendremos la fuerza resultante, cuya dirección va hacia la zona de menor presión.

Análisis de las líneas de corriente

Vamos a analizar las líneas de corriente del viento, es decir, las curvas que son tangenciales a la velocidad del viento en cada instante. Tendremos en cuenta el movimiento relativo de la pelota y la composición de velocidades.

En primer lugar analizamos el movimiento relativo de pelota-viento. Desde un punto de vista en tierra, el aire está quieto y es la pelota la que se mueve. Sin embargo, si situamos nuestro sistema de referencia en la pelota, observaríamos que la pelota está quieta y es el aire el que se mueve hacia ella. Este último punto de vista es más cómodo para estudiar las líneas de corriente.

Observamos que el comportamiento del viento es simétrico y se desplaza la misma parte de aire por ambos lados, siendo la resultante igual a 0. Es decir, la pelota va recta.

Sin embargo, entra en juego la rotación. La rotación produce un arrastre del aire de su alrededor, generando un movimiento de remolino con valor máximo en las proximidades de la pelota y que tiende a 0 a medida que nos alejamos.

El efecto curioso ocurre cuando se genera este remolino con la pelota en movimiento. Al sumarse el campo de velocidad del viento + el remolino, observamos que en una parte se acelera el viento (Sentido de giro y viento es el mismo) mientras que en la otra parte se desacelera (Sentido de giro es opuesto al del viento).

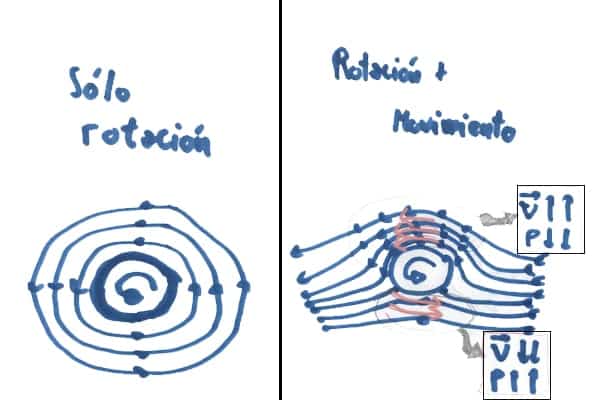
Esta diferencia de velocidades en el viento es, lo que mediante la ecuación de Bernoulli, nos da la información de la diferencia de presión y por lo tanto de la fuerza resultante sobre la pelota.

Esa es la explicación hablando de presiones y velocidades pero… ¿Se podría estudiar desde un punto de vista alternativo?

Efecto Magnus y 2ª Ley de Newton

Cómo no, en cualquier cosa que involucre el movimiento, Newton está presente. La cosa es que, desde un punto de vista más mecánico, el Efecto Magnus puede explicarse mediante la 2ª Ley de Newton.

Y no sólo el Efecto Magnus, sino que incluso la explicación de por qué vuela un avión (Cómo se genera sustentación en las alas) puede ser dada mediante dicha ley.

Cuando el balón avanza y se produce la variación de velocidades y presiones en el flujo, dicho flujo varía su trayectoria. A grandes rasgos le evolución del flujo es tal que así:

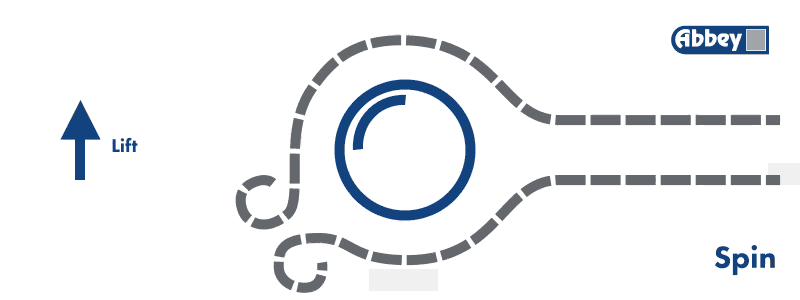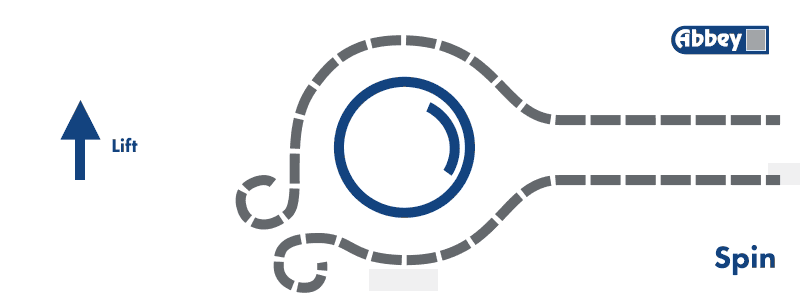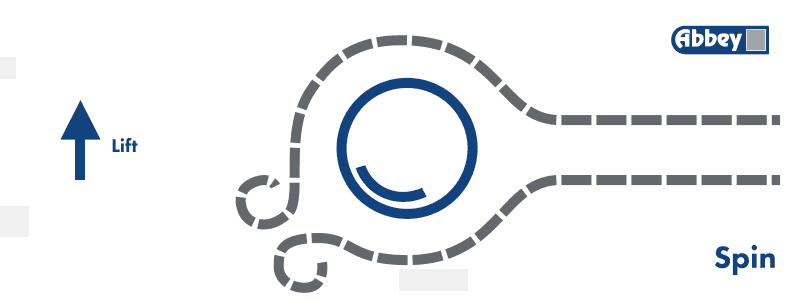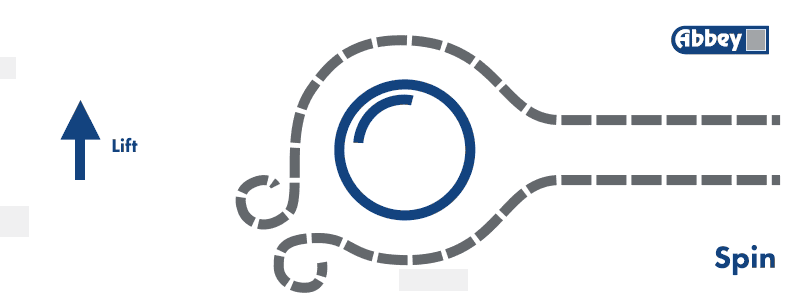
Es decir, que se desvía hacia una de las direcciones. Y… ¿Esto qué provoca?

\(\boxed{\vec{F}=m*\vec{a}=m*\frac{d\vec{v}}{dt}}\)

Que según la 2ª Ley de Newton, la pelota sufre una fuerza igual a la masa por la variación temporal de la velocidad. Si bien la velocidad puede que no varíe mucho su módulo, sí que varía si dirección, provocando una fuerza con dirección opuesta al desvío.

De hecho, que el viento pierda velocidad al impactar contra la pelota y se produzca una disminución de su módulo es lo que genera la fuerza de Drag o de “frenado” de la pelota, que es la que siempre actúa haya efecto Magnus o no (De lo contrario la pelota se movería indefinidamente)

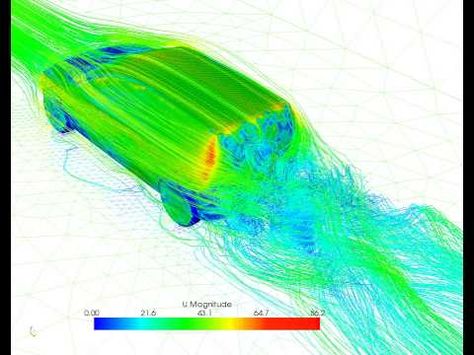
Volviendo a la animación de la pelota, observamos que la corriente se desvía parcialmente hacia abajo. Eso, como si de un propulsor se tratase, empuja la pelota hacia arriba, siendo esa fuerza conocida como lift o sustentación, y que mágicamente coincide con la resultante de la integral de la distribución de presiones alrededor de la pelota. (De hecho, de no coincidir en valor estaríamos en una paradoja física…)

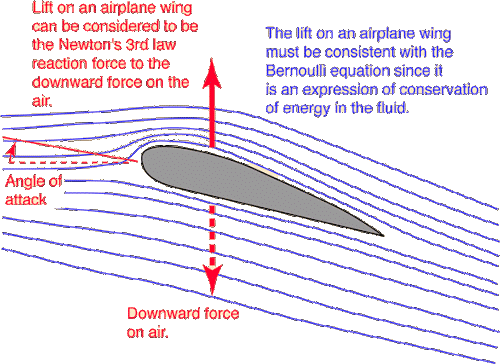
Algo similar ocurre con el ala de un avión, aunque no tiene NADA que ver con el Efecto Magnus. Por un cierto fenómeno (Al que le dedicaré un artículo), el aire es dirigido hacia abajo, y eso provoca que el ala sea empujado hacia arriba, siendo esta fuerza la sustentación.

Usos del Efecto Magnus

El efecto Magnus se emplea principalmente en los deportes. Deportes como el fútbol o el béisbol se aprovechan enormemente de este efecto para confundir al rival.

Otra de las aplicaciones de dicho efecto a nivel extra-deportivo es en el rotor Flettner, un sistema de propulsión para barcos que empleaba el efecto Magnus en una corriente perpendicular al barco para propulsarse. Aunque aparentemente parezca algo insignificante, la propulsión es 10 veces más potente que en la de un barco de vela convencional.

Por otro lado, una aplicación más bien experimental, es la de un avión que emplea el efecto Magnus para volar. Obviamente no es para nada útil en comparación a un avión con alas, pero es curioso: