Siempre que se celebran unas elecciones surge el debate acerca de la ley electoral y la forma de contabilizar los votos (Sistema o Ley d’Hont). Y este desacuerdo sucede cuando se comparan los escaños asignados a cada partido con el número de votos que recibió cada uno de ellos.
Si el partido A tiene el mismo número de votos que el partido B… ¿Por qué el partido A tiene casi el doble de escaños? O incluso partidos políticos como los independentistas con representación parlamentaria cuando tienen menos votos que otros partidos sin escaño.
En este artículo hablaré de cómo funciona la ley electoral en españa y en concreto de la Ley o Sistema d’Hont, un algoritmo que asigna escaños en función del número de votos.
Ley d’Hont
La Ley d’Hont es un algoritmo matemático que asigna los escaños de una determinada circunscripción partiendo del número de votos. Y antes de poder aplicar dicho algoritmo debemos de tener en cuenta 2 cosas que marca la ley electoral española (LOREG):
- Para que un partido político pueda participar en el reparto de escaños debe de haber obtenido más de un 3% del nº total de votos de dicha circunscripción.
- El número de escaños disponibles depende de la circunscripción (Provincia en el caso de elecciones generales)
Es decir, que en las elecciones generales el nº de votos de cada provincia (Circunscripción) es independiente del resto aunque luego tras saberse los resultados se sumen todos esos votos y se diga que X partido ha tenido un total de X votos.
Aquí puedes ver el número de escaños asignados a cada provincia.
Teniendo en cuenta dichas especificaciones y tras contabilizar los votos es posible asignar los escaños siguiendo la Ley d’Hont.
El algoritmo
Paralelo a la definición del algoritmo iré mostrando el ejemplo de elecciones en una provincia que puede repartir hasta 6 escaños a la que se presentaron 10 partidos políticos.
La forma de repartir los escaños es la siguiente:
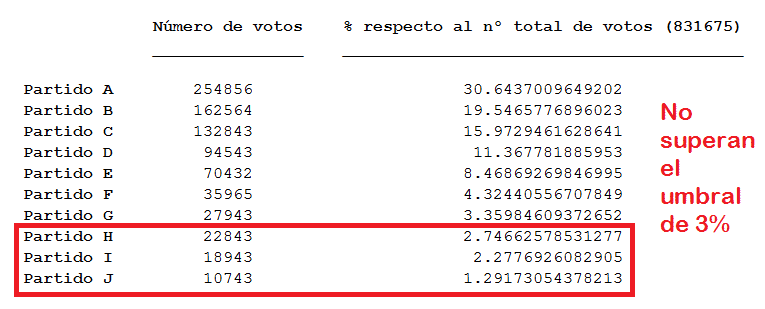
En primer lugar se ordenan los partidos por número de votos y se eliminan los partidos que no hayan superado la barrera del 3%
Posteriormente se crearán hasta n columnas (n=número de escaños disponibles) y en cada columna se irán colocando el número de votos de cada partido. En la columna 1 aparece el número de votos recibidos. En la 2 el número de votos entre 2. En la 3 el número de votos entre 3. Y así sucesivamente hasta la columna n.
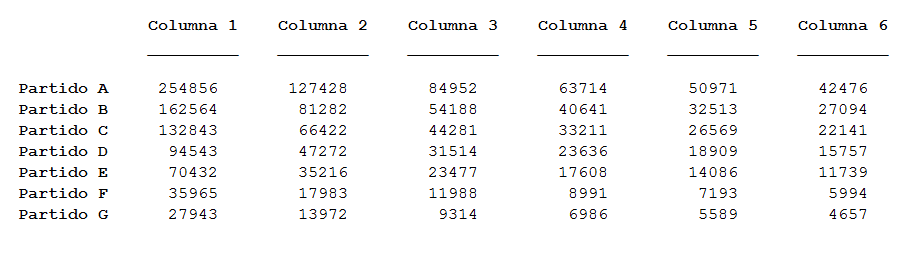
Finalmente, se buscan los n números más altos de la tabla y a dichas celdas se les asigna un escaño. De esa forma, el número de escaños asignado a cada partido será igual al número de escaños que sus celdas hayan obtenido.
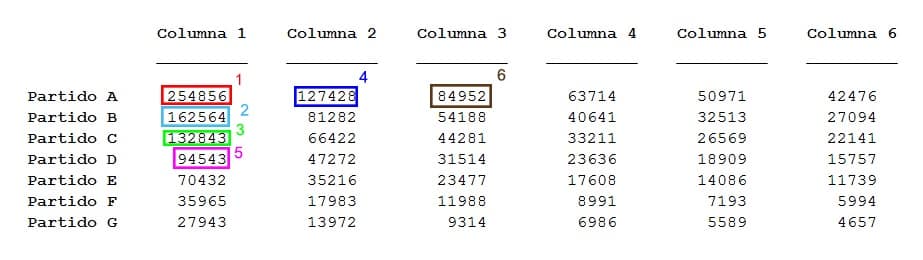
Observamos que el partido A ha obtenido 3 escaños mientras que los otros 3 escaños han sido adjudicados a los partidos B,C y D (1 para cada uno).
Es decir, que el partido A tiene el triple de escaños que el partido B cuando no tiene ni el doble de votos. Del mismo modo el partido B tiene el mismo número de escaños que el D y sin embargo tiene casi el doble de votos.
¿Es justo este sistema?
Efectividad de la Ley d’Hont
Como acabamos de observar quizás el reparto de escaños no es acorde con el número de votos recibido.
Pero… ¿De qué forma sería justo?
Supongamos que queremos equilibrar los escaños de nuestro ejemplo. Le quitamos un escaño al partido A, eso está claro. Pero… ¿A quién se lo damos?
- Si se lo damos al partido B, tendrían el mismo número de escaños A y B y sin embargo el partido A tiene 100.000 votos más que el partido B.
- Si se lo damos al partido E para fomentar la diversidad política este tendría el mismo número de escaños que B cuando el B tiene más del doble de votos…
Es decir, que sea como sea el reparto al final siempre hay algún partido perjudicado. Y el principal problema a la hora de repartir los escaños es que son enteros, es decir, que un partido no puede obtener 2,36 escaños, y por lo tanto siempre alguien sale beneficiado/perjudicado.
Además, votar en blanco no es del todo efectivo. Lo único que conseguimos es elevar el nº de votos totales y por ello se descartan los partidos minoritarios al no superar la barrera del 3%. Funcionaría únicamente si casi todo el mundo votase en blanco y hubiese partidos notorios sin escaños debido a no superar el umbral.
Votar en nulo y no votar es lo mismo.
- En las circunscripciones con un número reducido de escaños se ven beneficiados por la Ley d’Hont los partidos más grandes (Como se ha visto en el ejemplo)
- En las circunscripciones con un gran número de escaños disponibles el reparto es mucho más equitativo y ahí es donde cogen fuerza los partidos minoritarios.
Lo que no tiene nada que ver con la Ley d’Hont es el reparto de escaños por circunscripción. Esto se hace para facilitar la representación de ciertos partidos de regiones quizás algo olvidadas en el Parlamento (Teruel Existe, Coalición Canaria, partidos independentistas o vascos…) aunque bajo mi punto de vista es un fallo del sistema que las provincias aprovechan para obtener beneficios a cambio de votos y por eso cada vez salen más.
De hecho, llegará un momento en el que casi todas las provincias tendrán representación en el parlamento en forma de partido político y no podrán cambiar esta forma de dar escaños porque ningún partido regional iba a votar para ello.
Y tú, ¿Qué opinas del reparto de escaños? ¿Te parece injusto? ¿Qué cambiarías? ¡Cuéntalo en los comentarios!
Código de MATLAB para simular reparto de escaños
%Con este código puedes simular el reparto de escaños de m partidos
%políticos que optan a n escaños
%Si se quiere evitar introducir por pantalla el nº de votos puede
%sustituirse los input por matrices directamente
disp('Introduce números naturales o el programa dará error')
%Se introduce en m el número de partidos
m=input('Introduce el número de partidos: ');
votos=zeros(m,1);
%Se introduce en la matriz votos el nº de votos de cada partido
for i=1:m
votos(i,1)=input(sprintf('Introduce el nº de votos del partido %d: ', i));
end
disp('-')
disp('Esta es tu matriz de votos')
for i=1:m
fprintf('Partido %d: %d votos\n',i,votos(i))
end
disp('-')
%Se suman todos los votos y se divide cada fila para obtener en % de votos
%de cada partido y se rechazan los que tengan menos del 3%
S=sum(votos);
for i=1:m
if (votos(i)/S)<0.03
votos(i)=0;
end
end
%Se introduce en n el número de escaños a repartir
n=input('Introduce el número de escaños a repartir: ');
disp('-')
A=zeros(m,n);
%Se genera la matriz con los votos divididos entre 1,2,3,4... y
%posteriormente se buscan los valores más altos y se añade un
%contador a cada partido político con el nº de escaños asignados
for i=1:n
A(:,i)=votos./i;
end
contador=zeros(m,1);
maximo=max(A(:,1));
for t=1:n
maximo=0;
for i=1:m
for j=1:n
if A(i,j)>=maximo
maximo=A(i,j);
a=i;
b=j;
end
end
end
contador(a)=contador(a)+1;
A(a,b)=0;
end
disp('El reparto de votos es el siguiente:')
for i=1:m
fprintf('Partido %d: %d escaños\n',i,contador(i))
end