Demostración del movimiento oscilatorio. Muelles. Energía.

¡Buenas! En esta entrada os voy a hablar del movimiento oscilatorio y sus variantes. Comentaremos el movimiento armónico simple, el atenuado, y para finalizar deduciremos las ecuaciones del péndulo a partir de una linealización (Polinomio de Taylor despreciando términos de mayor orden)

Introducción

• Consideramos movimiento oscilatorio a todo aquel movimiento en el cual una misma posición de equilibrio se alcanza en repetidas (infinitas en el caso ideal) ocasiones, equiespaciados por un tiempo denominado periodo.
• Hablamos de movimiento armónico simple para referirnos a un movimiento periódico e infinito debido a que no consideramos fuerzas de rozamiento.
• En el caso de considerar fuerzas de rozamiento, estaríamos en el caso atenuado.

Hay que destacar que en todos los movimientos periódicos aparecen las funciones trigonométricas seno y coseno, esenciales en la dinámica.

En este artículo nos centraremos en los muelles, aunque el movimiento de los péndulos también se rige por dichas ecuaciones.

Movimiento armónico simple

Empezamos por el caso más sencillo de movimiento oscilatorio. Obtendremos el modelo matemático empleando la segunda ley de newton en forma de ecuaciones diferenciales y las integraremos, dejando indicado el valor de las constantes. Un sistema complejo como el de un péndulo que rota (2 grados de libertad) debería de ser analizado empleando las ecuaciones de Lagrange (Mecánica analítica). Consideraremos el caso de existencia e inexistencia de gravedad.

Muelle sin gravedad

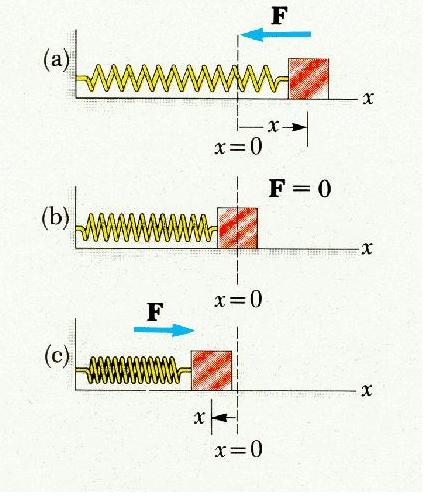
Para evitar el efecto de la gravedad podemos suponer un muelle horizontal con punto de equilibrio cuando x(t)=0. Debido a que sólo existe una dimensión en el movimiento (Eje x), trabajaremos con módulos referidos al vector unitario i en dirección al eje x.

La fuerza recuperadora es de la forma Fe=-kx (Si x es positivo [Muelle se alarga], el muelle hace fuerza hacia la izquierda [F<0]. Si x es negativo[Muelle se contrae], el muelle hace fuerza hacia la derecha [F>0]. La fuerza es proporcional a la deformación del muelle)

Aplicando la segunda ley de newton, se tiene que:

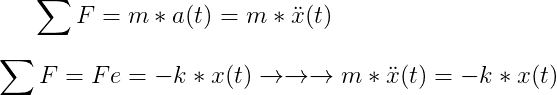
Despejando:

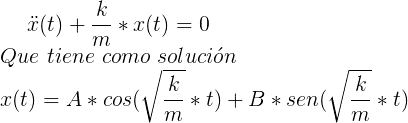
Tenemos que aplicar condiciones iniciales para poder calcular los valores de A y B. Supondremos el caso de que en t=0 el muelle se encuentra estirado 1m y que se encuentra justo en el punto de retroceso (Su velocidad es 0)

La solución queda:

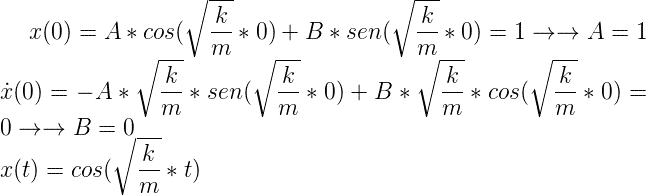
Observamos que el valor de x(t) comienza siendo 1 y va oscilando periódicamente desde 1 a -1, con un movimiento infinito debido a la inexistencia de rozamiento.

Muelle con gravedad

En este caso suponemos un muelle ideal vertical. Tomamos como punto de equilibrio y(t)=0 . Al igual que en el caso anterior, debido a la unidireccionalidad trabajaremos con módulos.

La fuerza recuperadora es de la forma Fe=-ky. La fuerza de la gravedad es Fg=-mg.

Aplicando la segunda ley de newton, se tiene que:

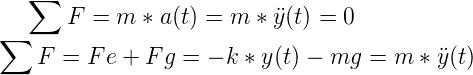
Despejando:

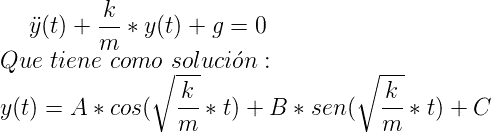
Para hallar el valor de C sustituimos los valores de y(t) teniendo en cuenta que y(t)=Yh(t)+Yp. Al cumplirse la solución oscilatoria de Yh(t) para todo t, únicamente debemos de sustituir el valor de Yp=C.

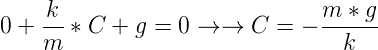
Tenemos que aplicar condiciones iniciales para poder calcular los valores de A y B. Supondremos el caso de que en t=0 el muelle se encuentra elevado a una altura de 1m y que se encuentra justo en el punto de retroceso (Su velocidad es 0).

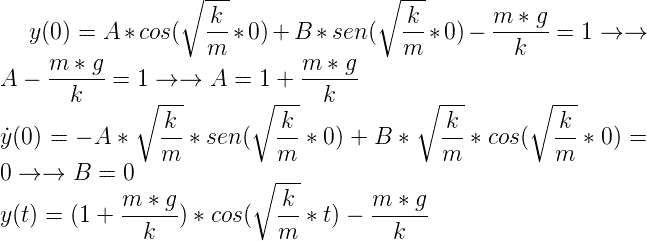
Observamos que los valores de y(t) oscilan entre 1 y \(-1-2*\frac{m*g}{k}\), estando el punto de equilibrio claramente desplazado hacia abajo debido al efecto de la gravedad.

Movimiento armónico amortiguado

En este caso haremos la misma deducción que en el caso del muelle horizontal pero con pérdidas. A pesar de ser el caso real algo muy temido entre los estudiantes, únicamente hay que añadir un término a la ecuación y mágicamente nos aparece un movimiento que se aproxima al comportamiento real de un muelle. En el caso vertical es exactamente igual pero, debido a la gravedad, el punto de equilibrio se desplazaría hacia abajo.

Así que, tomando como punto de equilibrio x(t)=0, con la fuerza recuperadora de la forma Fe=-k1x y una fuerza amortiguadora que se modela como Fa=-k2v, siendo v la velocidad de la masa durante su recorrido.

Aplicando la segunda ley de Newton:

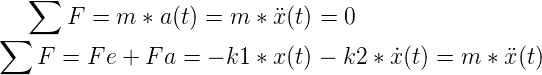
Despejando:

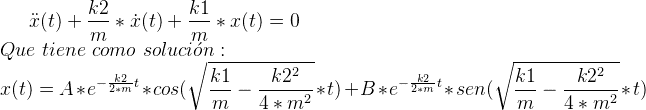
Queda una forma muy larga y que, para los que conozcan este movimiento, no les sonará. Para reducirla haremos un cambio de variable de la forma:

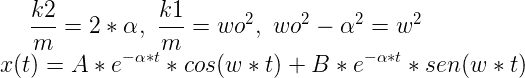
Aplicando condiciones iniciales tal que en t=0 el muelle se encuentra estirado 1m y que se encuentra justo en el punto de retroceso (Su velocidad es 0):

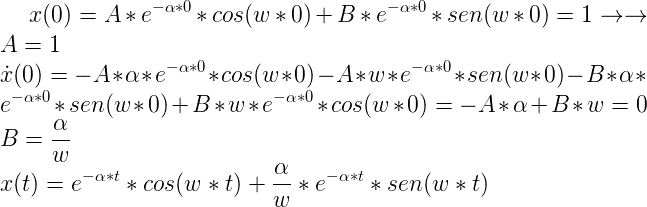
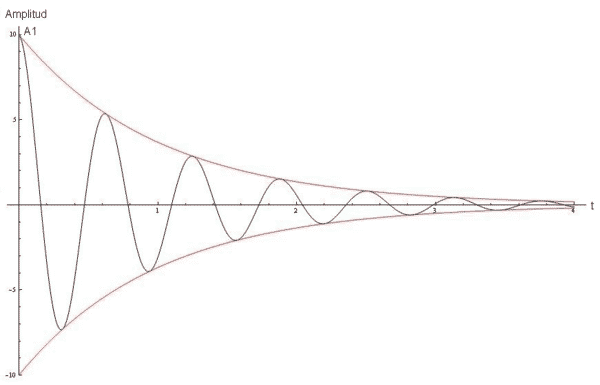
Observamos que el movimiento es muy similar al oscilatorio pero con un término amortiguador \(e^{-\alpha*t}\) que, en t=0 es 1 y a medida que aumenta el tiempo dicho término tiende a 0, atenuando el movimiento de la forma:

---

---

Energía

Una vez visto la deducción de los movimientos, vamos a analizar la energía de los casos amortiguados y sin amortiguar.

Para simplificar las expresiones, en vez de emplear el término \( A*cos(\sqrt{\frac{k}{m}}*t)+B*sen(\sqrt{\frac{k}{m}}*t)\) emplearemos la forma reducida \(I*cos(\sqrt{\frac{k}{m}}*t + C)\) que contiene la misma información.

Muelle ideal

Caso horizontal. La energía es la suma de la energía cinética + potencial

\(E=\frac{1}{2}*m*v^{2}+ \frac{1}{2}*k*x^{2}\)

Para completar los valores de la energía debemos de introducir nuestras expresiones de \(x(t) \ y \ \dot{x}(t)\)

\(\frac{1}{2}*m*(-I*\sqrt{\frac{k}{m}}*sen(\sqrt{\frac{k}{m}}*t+C))^{2} + \frac{1}{2}*k*( I*cos(\sqrt{\frac{k}{m}}*t + C) )^{2}\) \(\frac{k}{2}*I^{2}*sen^{2}(\sqrt{\frac{k}{m}}*t+C) + \frac{k}{2}* I^{2}* cos^{2}(\sqrt{\frac{k}{m}}*t+C)= \frac{k}{2}* I^{2} \)

Sorprendentemente y, como no podía ser de otra manera, la belleza de las matemáticas nos proporciona un valor constante \( \frac{k}{2} I^{2}\) como término constante de la energía de la masa unida al muelle; constante debido a que no hay pérdidas de energía. La I es una constante que representa la amplitud y se determina aplicando condiciones iniciales.

Conceptualmente la energía depende de cuanto alargamos el muelle y del tipo de muelle, ya que no contiene la misma energía estirar una goma elástica 1m a estirar 1m el muelle de un amortiguador.

Muelle real

Caso horizontal con rozamiento. La energía mecánica es la suma de la energía cinética + potencial.

\(x(t) = I \cdot e^{-\alpha t} \cdot \cos(w t + C)\)

\(v(t) = -I \cdot e^{-\alpha t} \cdot (\alpha \cos(w t + C) + w \sin(w t + C))\)

\(E = \frac{1}{2} m v^{2} + \frac{1}{2} k_1 x^{2}\)

\(E = \frac{1}{2} m I^{2} e^{-2 \alpha t} (\alpha^{2} \cos^{2}(w t + C) + (w^{2}-\alpha^{2}) \sin^{2}(w t + C)) + \alpha w \sin(2 w t + 2 C) + \frac{1}{2} k_1 I^{2} e^{-2 \alpha t} \cos^{2}(w t + C)\)

Siendo \(wo^{2}=\frac{k1}{m}\) agrupamos términos

\(E=\frac{1}{2}*k1*I^{2}*e^{-2*\alpha*t}+\frac{1}{2}*m*I^{2}*e^{-2*\alpha*t}*\alpha*(\alpha*cos(2*w*t+2*C)+w*sen(2*w*t+2*C))\)

Llegando a:

\(E=\frac{1}{2}*I^{2}*e^{-2*\alpha*t}*[k1+\frac{k2}{2} * (\alpha*cos(2*w*t+2*C)+w*sen(2*w*t+2*C))]\) \(E=\frac{1}{2}*I^{2}*e^{-2*\alpha*t}*(k1+G*cos(2*w*t+H)\)

Que, tomando valores arbitrarios, puede representarse respecto al tiempo generando una gráfica similar a:

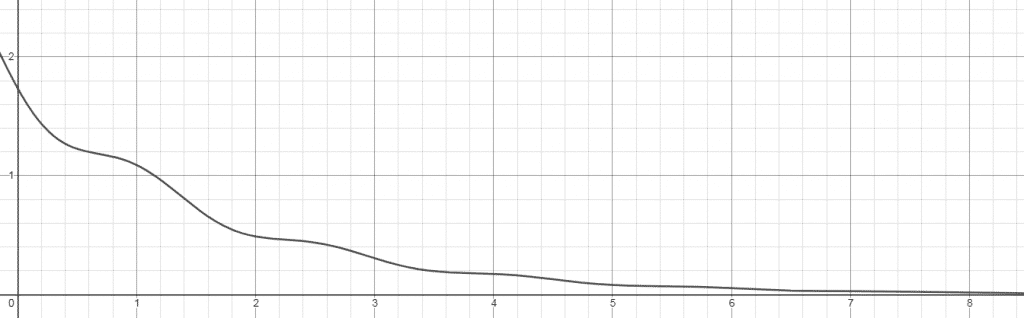
Observamos que el término exponencial hace que la energía vaya disminuyendo gradualmente. Especial atención a la oscilación aportada por el coseno. Las matemáticas no fallan ni dejan nada al azar. La aparición de dicho término en la ecuación es esencial y se debe al rozamiento.

Durante el movimiento, la energía se pierde debido a la fricción, la cual es proporcional a la velocidad del muelle. Así, en los «máximos» de las oscilaciones, el muelle se encuentra en la posición de velocidad 0 (Pasa de avanzar en una dirección a volver atrás) y como tal la energía no disminuye. No obstante, debido a la carrera de retorno la masa se acelera y la energía disminuye drásticamente hasta volver a encontrar otro punto de retorno.

También observamos que a medida que pasa el tiempo la energía disminuye más lentamente; esto se debe a que a menor velocidad la fricción es menor y como tal la energía disminuye a menor ritmo.