
Synkope, Projekt1, Flip Fly… Hay muchos nombres de atracciones de feria cuyo funcionamiento es el mismo: Un péndulo que a su vez rota.
En este artículo voy a hacer un análisis cinemático de dicha atracción de feria, calcular sus puntos notables (Cuando se alcanza la mayor/menor velocidad) y a jugar con ciertos valores como el par ejercido por el motor o las velocidades que se alcanzan.
Sin embargo, vamos a añadir una variación. Vamos a hacerlo más divertido, y es que en vez de rotar siempre en el mismo sentido, la rotación irá variando de forma periódica en el tiempo.
- El péndulo principal sufrirá un par que irá disminuyendo con el tiempo hasta dejar el movimiento oscilante libre.
- Sobre el disco se ejercerá un par oscilatorio que irá incrementando, de manera que se irá cambiando la dirección de giro de forma periódica con el tiempo.


Ecuaciones del movimiento
Para analizar el movimiento de un péndulo que rota debemos primero conocer qué movimientos están permitidos. Llegamos a la conclusión de que existen 2 grados de libertad, el del péndulo \(\phi\) y el de rotación del disco \(\theta\)
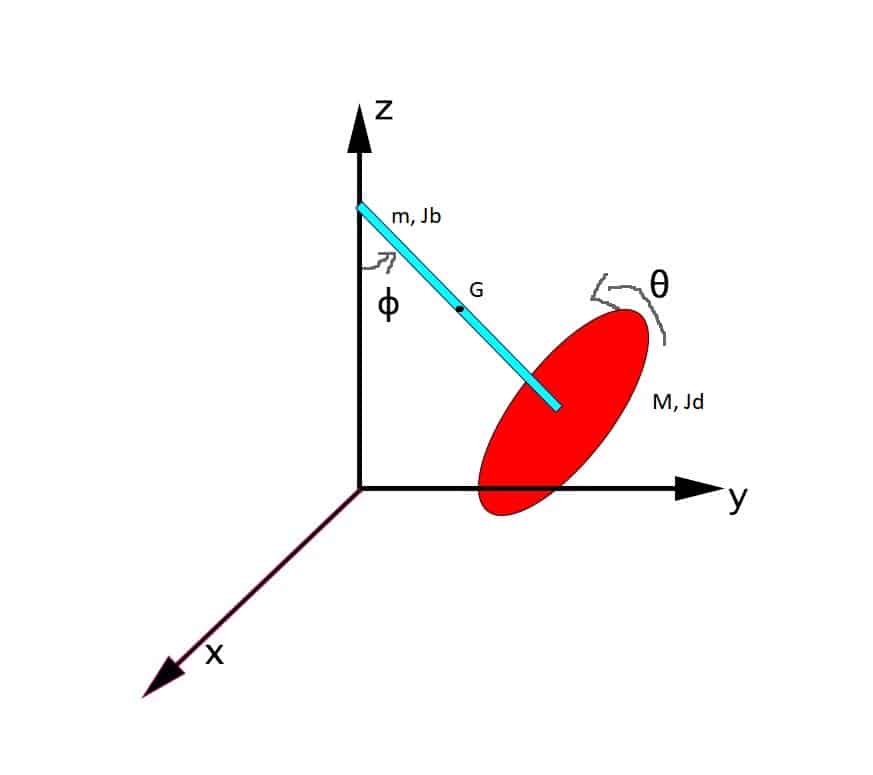
Este es un movimiento relativamente complejo, y es por ello que no emplearemos la mecánica newtoniana (Sumatorio de fuerzas y vectores). Emplearemos la mecánica analítica, que es una herramienta mucho más potente y matemática que hace que no tengamos que trabajar con vectores, sistemas de referencia o movimientos relativos. Todo son escalares que nos proporcionan la ecuación diferencial del movimiento directamente.

Mecánica analítica
Las ecuaciones básicas del movimiento son definidas por las ecuaciones de Lagrange, que aplicadas a nuestro sistema serían:
\(\frac{d}{dt}( \frac{\partial Ec}{\partial \dot{q_{i}}}) – \frac{\partial Ec}{\partial q_{i}} + \frac{ \partial V}{ \partial q_{i} } = Q_{i}\)
Siendo nuestras coordenadas generalizadas \(\phi\) y \(\theta\).
Ahora vamos a definir nuestras ecuaciones para la energía cinética, el potencial gravitatorio y la fuerza generalizada.
Energía cinética
Para la energía cinética de nuestro péndulo que rota debemos de considerar la suma de la energía cinética de la barra y del disco. Primero calculamos los momentos de inercia de barra y disco \(J_{b} , J_{d}\), así como el centro de gravedad G de la barra, que se encontrará en el punto medio.
- La masa del disco de radio R es M, y la de la barra, de longitud L, es m.
(Fórmulas conocidas, quizás en un artículo en el futuro explique cómo se calculan. Enlace a tabla de valores )
La energía cinética se compone de dos términos; el asociado a la velocidad del centro de gravedad, y el asociado a la rotación alrededor del centro de gravedad.
Nuestra fórmula queda:
\(E_c = \left[\frac{1}{2} M \cdot V_d^2 + \frac{1}{2} J_b \cdot \dot{\phi}^2\right] + \left[\frac{1}{2} m \cdot V_G^2 + \frac{1}{2} J_d \cdot \dot{\theta}^2\right]\)La velocidad del centro del disco \(V_{d}^{2}\) viene dada por \(V_d^2 = L^2 \cdot \dot{\phi}^2\)
La velocidad del centro de gravedad de la barra \(V_{G}^{2}\) viene dada por \(V_G^2 = \frac{L^2}{4} \cdot \dot{\phi}^2\)
Quedando nuestra ecuación de la energía cinética:
\(E_c = \left[\frac{1}{2} M \cdot L^2 \cdot \dot{\phi}^2 + \frac{1}{2} J_b \cdot \dot{\phi}^2\right] + \left[\frac{1}{2} m \cdot \frac{L^2}{4} \cdot \dot{\phi}^2 + \frac{1}{2} J_d \cdot \dot{\theta}^2\right] = \\\) \(= \frac{1}{2} \left( M \cdot L^{2} + J_{b} + m \cdot \frac{L^{2}}{4} \right) \cdot \dot{\phi}^{2} + \frac{1}{2} J_{d} \cdot \dot{\theta}^{2}\)Agrupando constantes, llegamos a una fórmula de la energía cinética de la forma:
\(E_c = \frac{1}{2} J^{*} \cdot \dot{\phi}^2 + \frac{1}{2} J_{d} \cdot \dot{\theta}^2 \)
Cálculo del potencial
Ahora vamos a calcular el potencial gravitatorio. Nuestro potencial es de la forma \(V=m*g*h_{G}+M*g*h_{d}\)
La altura del centro de gravedad de la barra es \(h_{G}=-\frac{L}{2}*cos(\phi)\)
La altura del centro de gravedad del disco es \(h_{d}=-L*cos(\phi)\)
Por lo tanto, \(V=m*g*( -\frac{L}{2}*cos(\phi) )+M*g*( -L*cos(\phi) )\)
Sin embargo, observamos que nuestro potencial no es lineal, ya que aparece nuestra coordenada \(\phi\) dentro de una función trigonométrica. Vamos a hacer un pequeño desarrollo de Taylor truncado al segundo término alrededor del punto de equilibrio \(\phi = 0\)
\(V(\phi) \approx V(0)+ [\frac{dV}{d\phi}|_{\phi=0}]*\phi + \frac{1}{2} [\frac{d^{2}V}{d\phi^{2}} |_{\phi=0}] *\phi^{2}\)- \(V(0)=-m*g*\frac{L}{2}-M*g*L\)
- \( \frac{dV}{d\phi}|_{\phi=0} = m*g*( \frac{L}{2}*sen(\phi = 0) )+M*g*(L*sen(\phi=0) ) =0\)
- \(\frac{d^{2}V}{d\phi^{2}} |_{\phi=0} = m*g*( \frac{L}{2}*cos(\phi = 0) )+M*g*(L*cos(\phi=0) ) = \)
Por lo tanto, agrupando términos, nuestro término de potencial linearizado queda de la forma:
\(V = -m*g*\frac{L}{2}-M*g*L + \frac{1}{2} (m*g* \frac{L}{2} + M*g*L ) *\phi^{2} = V^{*}*(\frac{1}{2}*\phi^{2}-1) \)\(V= V^{*}*(\frac{1}{2}*\phi^{2}-1) \)
Fuerza generalizada
Nos queda en último lugar definir el valor de la componente de la fuerza generalizada. Para ello empleamos el trabajo virtual \(\delta ^{*}\mathcal{L}= M_{\phi}*\delta \phi + M_{\theta}*\delta \theta\)
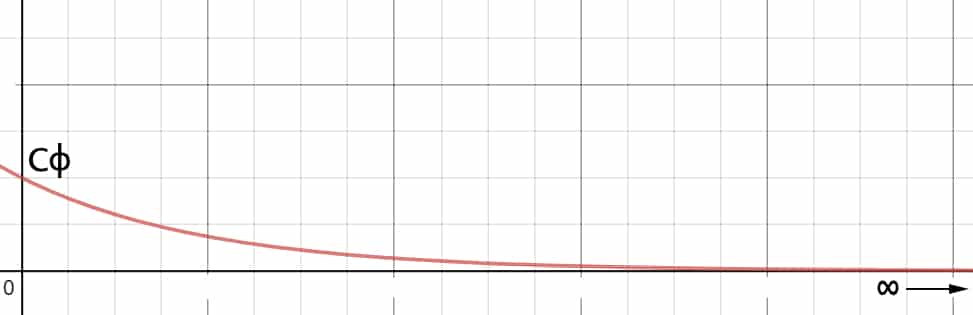
- Se ejerce un par \( M_{\phi} \) sobre la varilla que parte de un valor \(C_{\phi}\) que, con el tiempo, va disminuyendo hasta apagarse el motor, de manera que se deja un péndulo libre con cierta inercia.
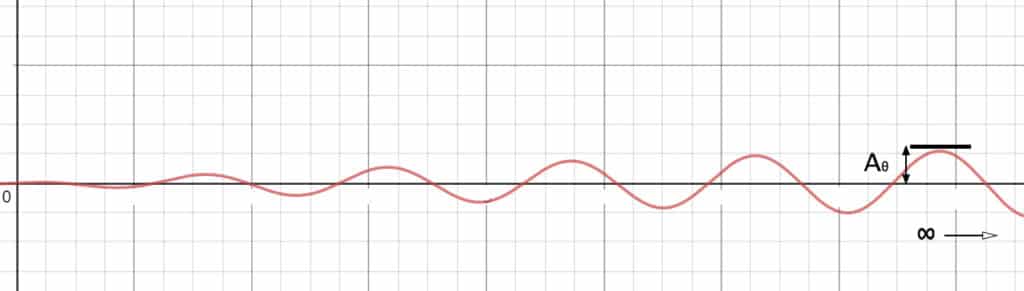
- Se ejerce un par \( M_{\theta} \) sobre el disco que parte desde 0 y que va aumentando con el tiempo, de manera que la frecuencia de las oscilaciones es constante en el tiempo pero cada vez tienen más amplitud, hasta llegar a una amplitud proporcional a \(A_{\theta}\)
De forma que;
\(Q_{\phi}=\frac{ \delta ^{*}\mathcal{L} }{ \delta \phi }= M_{\phi} \)
\(Q_{\theta}=\frac{ \delta ^{*}\mathcal{L} }{ \delta \theta }= M_{\theta} \)
Introduciendo todos los términos
Finalmente, aplicando las ecuaciones de Lagrange a los términos que hemos desarrollado, llegamos a
\(\phi: \frac{d}{dt}( \frac{\partial Ec}{\partial \dot{\phi}}) + \frac{ \partial V}{ \partial \phi} = Q_{\phi} \rightarrow \rightarrow J^{*}*\ddot{\phi} + V^{*}*\phi = C_{\phi}*e^{-w_{1}t} \)
\(\theta: \frac{d}{dt}( \frac{\partial Ec}{\partial \dot{\theta}}) + \frac{ \partial V}{ \partial \theta} = Q_{\theta} \rightarrow \rightarrow J_{d}*\ddot{\theta}= (1-e^{-w_{2}t})*A_{\theta}*cos(wt) \)
Que son las ecuaciones que definen los dos grados de libertad (Ángulos) del péndulo que rota que estamos estudiando.
Resolviendo la ecuación diferencial de phi

Nos encontramos con una ecuación diferencial lineal de segundo orden, cuya solución se compondrá de una solución homogénea + una solución particular
\(\phi(t)=\phi_{H}(t)+\phi_{P}(t)\)Cálculo de la solución homogénea
\(J^{*}*\ddot{\phi} + V^{*}*\phi=0\)Claramente la solución a esta ecuación homogénea es de la forma:
\(\phi_{H}(t)=A*cos(\sqrt{\frac{V^{*}}{J^{*}}}t)+B*sen(\sqrt{ \frac{V^{*}}{J^{*}} }t)\)Las constantes serán determinadas tras hallar la solución particular
Cálculo de la solución particular
\(J^{*}*\ddot{\phi} + V^{*}*\phi = C_{\phi}*e^{-w_{1}t} \)La solución particular será de la forma \(\phi_{P}(t)=K*e^{-w_{1}t}\)
Derivando e introduciendo en la ecuación:
\( J^{*} *K*w_{1}^{2} *e^{-w_{1}}+ V^{*}* K*e^{-w_{1}t} = C_{\phi}*e^{-w_{1}t} \rightarrow K=\frac{C_{\phi}}{ J^{*}* w_{1}^{2} + V^{*}}\)Imponemos las condiciones iniciales de ángulo y velocidad 0 en el inicio para calcular las constantes A y B:
\(\phi(t)= A*cos(\sqrt{\frac{V^{*}}{J^{*}}}t)+B*sen(\sqrt{\frac{V^{*}}{J^{*}} }t) + \frac{C_{\phi}}{ J^{*}* (w_{1})^{2} + V^{*}} * e^{-w_{1}t} \) \(\phi(0)=A+ \frac{C_{\phi}}{ J^{*}* (w_{1})^{2} + V^{*}} =0 \rightarrow A=- \frac{C_{\phi}}{ J^{*}* (w_{1})^{2} + V^{*}} \) \(\dot{\phi}(0) = B \cdot \sqrt{\frac{V^{*}}{J^{*}}} – w_{1} \cdot \frac{C_{\phi}}{J^{*} \cdot (w_{1})^{2} + V^{*}} = 0 \rightarrow B = \sqrt{\frac{J^{*}}{V^{*}}} \cdot w_{1} \cdot \frac{C_{\phi}}{J^{*} \cdot (w_{1})^{2} + V^{*}}\)La evolución de nuestro ángulo \(\phi(t)\) será:
\(\phi(t)= – \frac{C_{\phi}}{ J^{*}* (w_{1})^{2} + V^{*}} * cos(\sqrt(\frac{V^{*}}{J^{*}})t) + \sqrt(\frac {J^{*}}{V^{*}}) *w_{1}* \frac{C_{\phi}}{ J^{*}* (w_{1})^{2} + V^{*}} * sen(\sqrt(\frac{V^{*}}{J^{*}})t) + \frac{C_{\phi}}{ J^{*}* (w_{1})^{2} + V^{*}} * e^{-w_{1}t} \)Uniendo términos:
\(\phi(t)= \frac{C_{\phi}}{ J^{*}* (w_{1})^{2} + V^{*}} *[\sqrt(\frac {J^{*}}{V^{*}}) *w_{1}* sen(\sqrt(\frac{V^{*}}{J^{*}})t) – cos(\sqrt(\frac{V^{*}}{J^{*}})t) + e^{-w_{1}t} ] \)
Hallando la forma de theta

Cálculo de la solución homogénea
\(J_{d}*\ddot{\theta}=0 \)Al igual que antes, esta ecuación tiene una solución inmediata de la forma:
\(\theta_{H}(t)=A*t+B\)Cálculo de la solución particular
La solución particular será de la forma \(\theta_{P}=\theta_{P_{1}}+ \theta_{P_{2}} \) con
\( \theta_{P_{1}}=A*cos(wt)+B*sen(wt) \) \( \theta_{P_{2}} = e^{-w_{2}t}*[C*cos(wt)+D*sen(wt)]\)Y las ecuaciones a resolver:
- \(J_{d}*\ddot{\theta}_{P_{1}}=A_{\theta}*cos(wt)\)
- \(J_{d}*\ddot{\theta}_{P_{2}}=-e^{-w_{2}t}*A_{\theta}*cos(wt)\)
Calculando las constantes A,B,C y D llegamos a la solución particular \(\theta_{P}\):
\(\theta_{P}=-(\frac{A_{\theta}}{J_{d}*w^{2}}+\frac{1}{ J_{d} }\frac{A_{\theta}*(w_{2}^{2}-w^{2})}{ (w_{2}^{2}-w^{2}) +4*w^{2}*w_{2}^{2}}*e^{-w_{2}t})*cos(wt)+ \) \(+ \frac{1}{ J_{d} } \frac{2*A_{\theta}*w*w_{2}}{ (w_{2}^{2}-w^{2}) +4*w^{2}*w_{2}^{2}}*e^{-w_{2}t}*sen(wt) \)Llegados a este punto observamos que si \(w=w_{2}\) nuestro valor de \(\theta(t)\) se simplifica muchísimo. Lo mismo ocurre para \(\phi(t)\) haciendo \(w_{1}= \sqrt(\frac{V^{*}}{J^{*}})\), que es la frecuencia característica de nuestro péndulo.
Para un valor de \(t=\frac{1}{w}\) se habría alcanzado el 63% de la amplitud del permanente (\(1-e^{-1}\approx 0.63\)), siendo para el caso \(t=\frac{3}{w}\) un valor del 95%.
Por ello, para poder expresar un valor de \(\theta\) simple pero aún así realista, tomamos dicho valor. De esta forma, y tras calcular el valor de las constantes A y B llegamos a:
\(\theta(t)= \frac{A_{\theta}}{J_{d}*w_{2}^{2}}*(1-cos(w_{2}t))+ \frac{A_{\theta}}{2*J_{d}*w_{2}^{2}}*e^{-w_{2}t}*sen(w_{2}t) \)
Organizando las ecuaciones del péndulo que rota
Nuestras ecuaciones son:
\(\phi(t)= \frac{C_{\phi}}{ 2*V^{*}} *[ sen(\sqrt(\frac{V^{*}}{J^{*}})t) – cos(\sqrt(\frac{V^{*}}{J^{*}})t) + e^{- \sqrt(\frac{V^{*}}{J^{*}})t } ] \)
\(\theta(t)= \frac{A_{\theta}}{J_{d}*w_{2}^{2}}*[1-cos(w_{2}t)+ \frac{e^{-w_{2}t}}{2}*sen(w_{2}t) ] \)
\(\dot{\phi}(t)= \frac{C_{\phi}}{2* V^{*}} * \sqrt(\frac{V^{*}}{J^{*}}) *( cos( \sqrt(\frac{V^{*}}{J^{*}})t) + sen( \sqrt(\frac{V^{*}}{J^{*}} )t)-e^{ – \sqrt(\frac{V^{*}}{J^{*}}) t }] \)
\(\dot{\theta}(t) = \frac{A_{\theta}}{J_{d} \cdot w_{2}} \left(\sin(w_{2}t) + \frac{e^{-w_{2}t}}{2} \cdot (\cos(w_{2}t) – \sin(w_{2}t))\right)\)
Análisis ingenierístico del resultado

Antes de nada hay que analizar el resultado y ver si es coherente. Y para ello tenemos que tener en cuenta el detalle importante de que el movimiento de ambos cuerpos es periódico.
Es por ello que, el ángulo recorrido debería de ser finito para un tiempo infinito. Observamos que todos los términos aparecen multiplicados por funciones trigonométricas, aunque unos con más amplitud que otro… ¿Cómo influye al ángulo recorrido?
Al existir esa fuerza inicial, habrá un movimiento en el inicio preferente hacia una de las direcciones (Hacia la que empuja la fuerza), desplazando el punto de equilibrio del sistema hacia otro punto. Es por ello que el ángulo para valores bajos de t tenderá a ser positivo o negativo a pesar de la oscilación.
Sin embargo, vamos a analizar el problema una vez ha pasado un tiempo bastante grande y ya nuestra máquina se encuentra en movimiento completamente oscilatorio con los motores apagados. \(\lim_{t \to \infty}(e^{-wt})=0\)
Nuestras ecuaciones resultan:
\(\phi(t)= \frac{C_{\phi}}{ 2*V^{*}} *[ sen(\sqrt(\frac{V^{*}}{J^{*}})t) – cos(\sqrt(\frac{V^{*}}{J^{*}})t) ] = -\frac{\sqrt2 *C_{\phi}}{ 2*V^{*}} *cos (\sqrt(\frac{V^{*}}{J^{*}})t+\frac{\pi}{4}) \)
\(\theta(t)= \frac{A_{\theta}}{J_{d}*w_{2}^{2}}*[1-cos(w_{2}t)] \)
\(\dot{\phi}(t)= \frac{ \sqrt2 * C_{\phi}}{2* V^{*}} * \sqrt(\frac{V^{*}}{J^{*}}) * sen( \sqrt(\frac{V^{*}}{J^{*}})t +\frac{\pi}{4}) \)
\(\dot{\theta}(t) = \frac{A_{\theta}}{J_{d} \cdot w_{2}} \sin(w_{2}t)\)
Observamos que tras unir las funciones trigonométricas y quitar la fase transitoria se obtiene una forma mucho más limpia, donde claramente vemos la amplitud de ambas rotaciones en función de la masa, dimensiones y par inicial aplicado por el motor.
Velocidad de un punto en el extremo del disco
Vamos a computar la velocidad en un punto situado en el extremo del disco. A partir de la fórmula que obtengamos podremos calcular los valores del tiempo en el que se obtienen las máximas y mínimas velocidades.
Primero calculamos la velocidad vectorial como la suma de la velocidad del péndulo y la de rotación, estando el vaivén del péndulo en el plano x=0 y la rotación alrededor del eje (Hola de nuevo, Newton):

La posición del punto extremo P viene dada por:
\(\vec{OP}=[(Rcos\theta\vec{i} ,(Lsen\phi+Rsen\theta \cos\phi) \vec{j} ,(L(1-cos\phi)+Rsen\theta sen\phi)\vec{k}]\)
Si la intentamos derivar llegamos a……..:
\(\vec{V}=(-R\dot{\theta}sen\theta )\vec{i} +\)
\(+(L\dot{\phi}cos\phi + R \dot{\theta} cos\theta cos\phi – \dot{\phi} cos\theta sen\phi )\vec{j}+\)
\(+( L\dot{\phi}sen\phi + R \dot{\theta} cos\theta sen\phi + \dot{\phi} sen\theta cos\phi )\vec{k}\)
Observamos que es una expresión tremendamente larga, y es inviable intentar calcular su módulo y expresarlo de forma simbólica. Vamos a analizar un caso más simple y calcularemos la velocidad en los puntos directamente.
Caso simple del péndulo que rota con la misma frecuencia
Consideraremos las ecuaciones sin transitorio desde el inicio, de manera que podemos acoplar el movimiento de giro de ambas rotaciones sin que el movimiento se vuelva caótico. La frecuencia característica de la rotación del disco será igual a la del péndulo, de forma que cuando el péndulo vaya de izquierda a derecha el disco girará en sentido antihorario, y cuando vaya de derecha a izquierda lo hará en sentido horario.
Además, en nuestro péndulo que rota impondremos la condición de que al llegar a la posición de mayor altura nuestro disco haya recorrido \(\pm \frac{\pi}{2}\) radianes
Ecuaciones
\(\phi(t)= \frac{K_{\phi}}{ V^{*}} *sen (\sqrt(\frac{V^{*}}{J^{*}})t) \)
\(\theta(t)= \frac{\pi}{2}*sen( \sqrt(\frac{V^{*}}{J^{*}}) t) \)
\(\dot{\phi}(t)= \frac{K_{\phi}}{ V^{*}} \cdot \sqrt{\frac{V^{*}}{J^{*}}} \cdot \cos\left(\sqrt{\frac{V^{*}}{J^{*}}} \cdot t\right) \)
\(\dot{\theta}(t) = \frac{\pi}{2} \cdot \sqrt{\frac{V^{*}}{J^{*}}} \cdot \cos\left(\sqrt{\frac{V^{*}}{J^{*}}} \cdot t\right)\)
Que cumplen las ecuaciones de:
\( J^{*}*\ddot{\phi} + V^{*}*\phi = 0 \) , con una inercia inicial que proporciona una amplitud de \( \frac{K_{\phi}}{ V^{*}} \)
\( J_{d}*\ddot{\theta}= – \frac{\pi}{2} *\frac{V^{*}*J_{d}}{J^{*}}*sen( \sqrt(\frac{V^{*}}{J^{*}}) t) \), tras hacer \(A_{\theta}= \frac{\pi}{2} *\frac{V^{*}*J_{d}}{J^{*}} \)
Cálculo de la velocidad
Máxima velocidad
Según nuestras condiciones iniciales, la máxima velocidad se alcanza con el péndulo completamente hacia abajo y con el disco en la posición inicial, es decir, \(\phi = \theta = 0\). Esto se alcanza en los tiempos \(t_{n}=n\pi\sqrt{\frac{J^{*}}{V^{*}}} \rightarrow \theta( t_{n} )=\phi( t_{n} )=0\), con n=0,1,2,3…
\(\vec{V_{max}}=(L\dot{\phi} + R \dot{\theta} )\vec{j} \)
Introduciendo nuestros valores y poniendo el módulo:
\(V_{max}=L \frac{K_{\phi}}{ V^{*}} * \sqrt(\frac{V^{*}}{J^{*}}) * cos( \sqrt(\frac{V^{*}}{J^{*}})t=t_{n} ) + R \frac{\pi}{2} * \sqrt(\frac{V^{*}}{J^{*}}) *cos( \sqrt(\frac{V^{*}}{J^{*}}) t=t_{n}) \)\( V_{max}= \sqrt{\frac{V^{*}}{J^{*}}}*(L \frac{K_{\phi}}{ V^{*}}+ R \frac{\pi}{2}) \)
Mínima velocidad {v=0}
La mínima velocidad se alcanzará cuando el péndulo esté en su máxima altura y el disco esté a punto de invertir su giro, es decir, \(\dot{\phi} = \dot{\theta} = 0\)
Observamos que para \(t_{n}=(2n-1)\frac{\pi}{2}\sqrt{\frac{J^{*}}{V^{*}}}\), con n=1,2,3… \(\rightarrow \dot{\theta}(t_{n})= \dot{\phi}(t_{n}) =0\)
Todos los términos de la velocidad vienen multiplicados por la velocidad angular. Por ello, sabemos que el módulo de la velocidad es
\(V_{min}=0\)
Esto ocurre cuando el péndulo llega a los puntos de mayor altura. Hay que destacar que, al tener la misma frecuencia que la rotación del disco, en esos puntos el disco se encuentra a velocidad 0 cambiando su sentido de giro. Por lo tanto la velocidad total es nula.
Conclusiones
Ahí están las ecuaciones. Únicamente tendríamos que emplear un programa informático (Matlab) e introducir los valores de las masas y dimensiones para obtener diferentes valores de velocidad o aceleración de los puntos en función del tiempo/posición de un péndulo que rota.
Hemos despreciado en todo momento el efecto de la fricción. No obstante, eso no quiere decir que nuestro resultado no sea verdadero. De forma oculta hemos aplicado la condición de que nuestro motor ejerce adicionalmente y durante todo el tiempo una potencia igual a la potencia disipada por el rozamiento, de manera que ambos términos se cancelarían de la ecuación (Que es precisamente lo que hace el «Control Automático»)
Se podría hacer un análisis mucho más exhaustivo, y añadir preguntas como los esfuerzos que soporta la estructura en todo momento, así como la fuerza o los «g» que experimentaríamos al estar dentro.
Sin embargo, requeriría tiempo del que no dispongo actualmente. Dejo la puerta abierta. Si has llegado a este punto te agradezco enormemente haber leído el artículo y pido disculpas por haberlo hecho «demasiado matemático», distinto al tipo de artículos que hago últimamente. Si te ha gustado, tengo dos artículos similares:


Un artículo muy denso y trabajado, enhorabuena!