🥫 ¿Por qué las latas tienen ese tamaño? Latas alargadas vs clásicas

Probablemente muchos se hayan preguntado por qué las latas tienen la forma y dimensiones a las que estamos acostumbrados: para una lata de 330ml es de aproximadamente 6cm de diámetro y 12cm de altura.

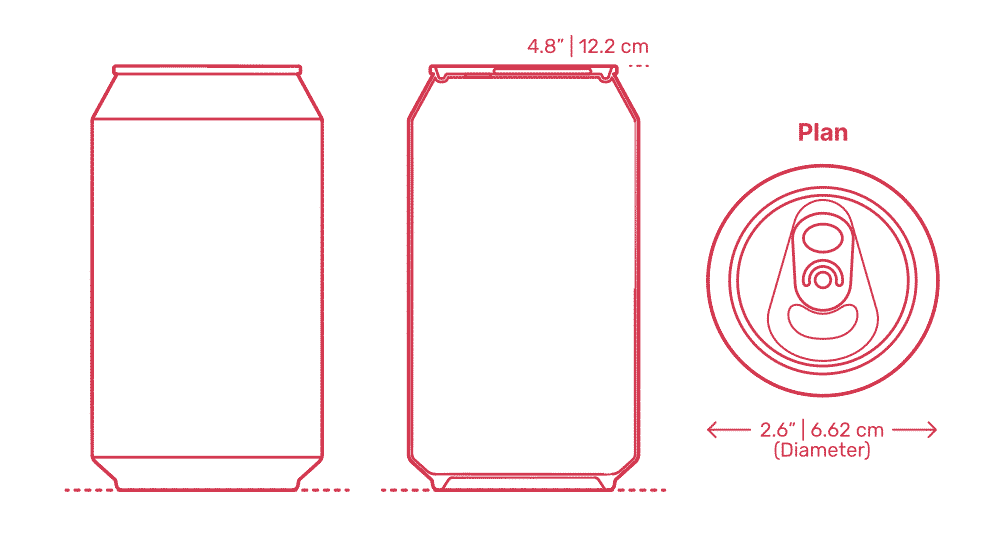
Obviamente una primera respuesta es: haces una lata que sea cómoda de agarrar de forma que fijas su diámetro, y luego le metes una altura tal que al final la lata tenga el volumen deseado.

Sin embargo, eso no es lo único que influye. Por un lado influyen las proporciones ya que en función de que la lata sea más o menos compacta será necesario emplear más o menos aluminio en la lata, y por otro lado la forma afecta a las propiedades mecánicas y a la estabilidad de la lata: una lata muy delgada será muy débil mecánicamente e inestable.

En este artículo hablaré del por qué de la forma de las latas de bebida y a qué afecta cada decisión. Además, haré un desarrollo matemático demostrando cuál sería el tamaño óptimo de una lata que minimiza la cantidad de material empleado en ella. De esa manera se podrá poner fin al debate iniciado contra mi amigo Alfonso de si una lata gorda con el mismo volumen que una delgada tiene el mismo material o no.

Por qué las latas son cilíndricas

Cada segundo se producen 6700 latas, lo que es equivalente a aproximadamente 200 mil millones de latas al año. Dichas latas se fabrican en la mayoría de los casos con aluminio.

El aluminio es el metal más costoso en términos energéticos de producir. Si bien el aluminio se encuentra por todas partes (es el metal más abundante), este se encuentra en estado natural formando óxidos. El enlace que forma el aluminio con el oxígeno es tan potente que es necesario aplicar una gran energía en el proceso de electrolisis para obtener aluminio puro.

Una tonelada de aluminio en bruto requiere de 17.000 kWh para ser procesado, es decir, se requieren 17 kWh por cada kilogramo de aluminio. Para hacernos una idea, 1 litro de gasolina puede generar en torno a 9 kWh, es decir, que por cada kilogramo que se produce de aluminio es necesario emplear una cantidad elevadísima de energía. De hecho, el 1-2% de la energía eléctrica mundial se emplea para procesar aluminio.

Dado el elevado coste del aluminio y la elevada producción de latas uno se da cuenta de que el diseño de una lata no debe ser puro azar, puesto que un pequeño cambio que suponga 1g de aluminio más en una lata supone miles de millones de euros al año. Entonces… ¿Por qué forma cilíndrica y por qué esas proporciones?

Si un ingeniero tuviese que diseñar una lata sabiendo todo lo anterior se decantaría rápidamente por una forma esférica: es la forma que permite almacenar el máximo volumen empleando la mínima superficie, es decir, reduciendo al máximo el material necesario, y además al estar la presión ejercida simétricamente en toda la superficie interna se garantizan buenas propiedades mecánicas.

Sin embargo, una esfera no es práctica en términos de fabricación y además su inestabilidad haría que la lata volcase derramando el contenido. Por otra parte, en términos de almacenaje (aspecto importantísimo en logística y que mueve miles de millones de euros al año) una esfera tampoco es eficiente porque sólo tiene un 74% de factor de almacenamiento.

La alternativa opuesta sería una lata cúbica, que no tendría el problema de la inestabilidad, sería mucho más fácil de fabricar que una esfera y además tendría un 100% de factor de almacenamiento. Sin embargo, las “esquinas” y bordes agudos supondrían un problema importante en términos mecánicos y habría que emplear más material de la cuenta para el mismo volumen.

Un cilindro es una mezcla de ambas soluciones: tiene un gran factor de almacenamiento (91%) y es muy sencillo de fabricar. Además, es cómodo para beber y estable. Si bien no presenta una simetría infinita como la esfera sino que únicamente una simetría radial, añadiendo una cúpula en la base y redondeando las aristas se puede simular el estado de membrana mediante el cuál la presión interna de la lata aumenta la rigidez y por lo tanto evita que la lata se deforme.

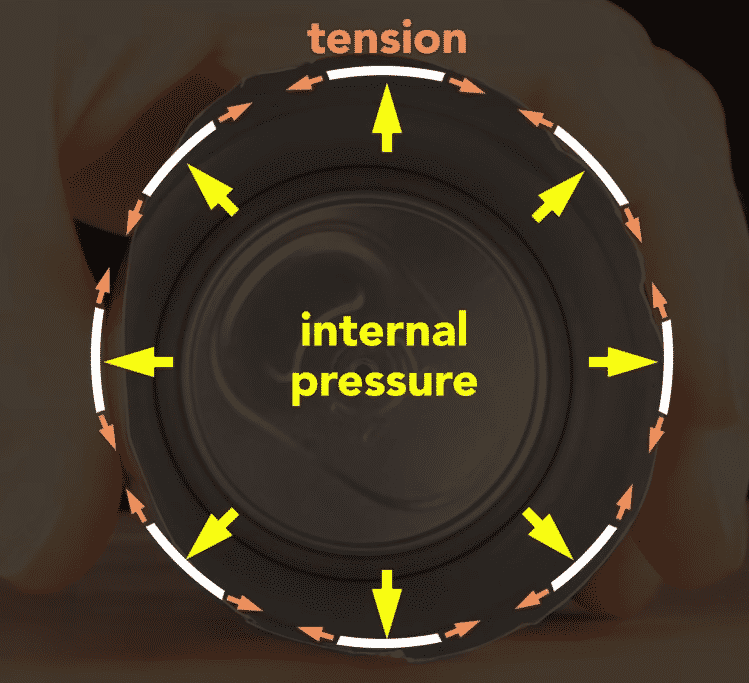
Una vez definida la forma, queda por elegir las dimensiones. Lo único que nos queda por optimizar es la relación entre altura del cilindro y radio de la base que permita almacenar el máximo volumen de líquido empleando la menor superficie posible.

Proporciones que minimizan la superficie de un cilindro

Para empezar se realiza una simplificación clara: para la lata se asume un cilindro perfecto. Es decir, que no se consideran los bordes suaves ni la cúpula de la base. Esta hipótesis puede hacerse porque a efectos comparativos (que es lo que se busca en este artículo) no afecta entre latas similares ya que se cancela el volumen despreciado.

Vamos a ser analíticos: nuestro problema a resolver es calcular la altura \(h\) y el radio del cilindro \(r\) que permiten, para un volumen \(V\) fijo, emplear la menor superficie \(S\) posible.

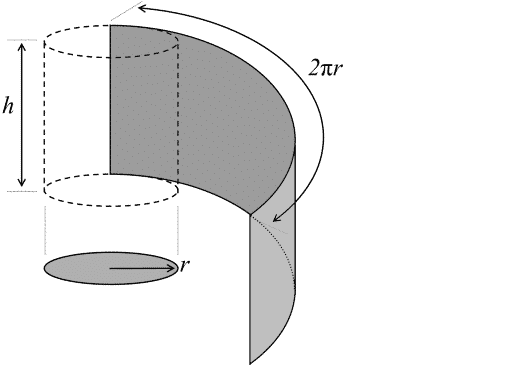
Es decir, un problema de optimización en el que se implican 2 variables \((h,r)\), hay una restricción en volumen \(V\) y la función a optimizar es la superficie \(S\). El problema tiene solución.

\(V=\pi r^{2} h\)

\(S(h,r)=2 \pi r h + 2 \pi r^{2}\)

Tomando\(V\) como constante, podemos expresar la altura en función del radio:

\(h = \dfrac{V}{\pi r^{2}}\)

Sustituyendo en la función \(S(h(r),r) = S(r)\), nos queda una función a optimizar con una única variable, no siendo necesario aplicar un método de optimización multivariable como el de los multiplicadores de Lagrange. Con derivar e igualar a \(0\) se encuentran los extremos relativos.

\(S(r)=\dfrac{2 V}{r} + 2 \pi r^{2}\)

\(\dfrac{dS}{dr} = – \dfrac{2 V}{r^{2}} + 4 \pi r = 0 \rightarrow \)

\(\rightarrow 4 \pi r^{3} – 2V=0 \rightarrow \boxed{r_{min} = \sqrt[3]{\dfrac{V}{2 \pi}}}\)

Debe ser un mínimo puesto que no hay un máximo acotado: es posible tener superficie infinita haciendo el cilindro extremadamente delgado o extremadamente gordo. Igualmente puede comprobarse fácilmente observando su curvatura con la derivada segunda:

\(\dfrac{d^{2} S}{dr^{2}} = \dfrac{4 V}{r^{3}} + 4 \pi\)

Introduciendo el \(r_{min}\):

\(\dfrac{d^{2} S}{dr^{2}} = \dfrac{4 V}{\dfrac{V}{2 \pi}} + 4 \pi = 12 \pi > 0\)

Por lo que se confirma que es un mínimo. Para obtener la altura a la que se corresponde dicho radio mínimo basta con expresar una variable en función de la otra:

\(h_{min} = \dfrac{V}{\pi r^{2}_{min}} = \dfrac{V}{\pi \left ( \sqrt[3]{\dfrac{V}{2 \pi}} \right )^{2}} = 2 \sqrt[3]{\dfrac{V}{2 \pi}} = 2 r_{min}\)

Es decir, que la superficie mínima de un cilindro se obtiene cuando su altura es igual a su diámetro

\(\boxed{h=2r, \rightarrow \dfrac{h}{r}=2}\)

Tiene sentido que no dependa del volumen ya que las proporciones se mantienen constantes. También tiene sentido la solución porque cuanto más similar a una esfera sea un cuerpo, más compacto será.

Si quisiésemos una lata óptima para almacenar 330ml deberíamos de emplear un volumen tal que:

\(330 = V(h=2r) = 2 \pi r^{3} \rightarrow r = 3.745\)

Es decir, una lata con una altura y diámetro de 7.49 centímetros. Esto supondría una lata un poco más gorda y sobre todo menos alargada a lo que estamos acostumbrados. Entonces… ¿Por qué están las empresas perdiendo tantos millones de euros en aluminio?

Vale, he exagerado un poco. La cantidad de aluminio presente en la lata encarece o abarata el producto, pero en su fabricación influyen muchísimos otros factores. Tener una cadena logística más eficiente, emplear menos recursos en la bebida o básicamente hacer un producto más atractivo que asegure más ventas permite que los beneficios superen con creces a lo que se pierde en material.

• En función del tipo de alimento o bebida se empleará una lata u otra. Una lata que contenga alimentos para coger con los dedos va a ser en general más ancha que alta para que el usuario no tenga dificultades a la hora de meter los dedos. Lo mismo ocurre con una lata de bebida: estamos acostumbrados a que las latas tengan un diámetro cómodo en las manos de cualquier persona (desde un niño a un adulto con las manos grandes) y una lata que tuviera un diámetro diferente se sentiría incómodo. Por eso, las compañías optan por mantener el diámetro y simplemente aumentar la altura en caso de querer introducir más o menos cantidad de producto.
• Las latas no se venden o almacenan individualmente sino en grupos. Tener latas con una relación en sus proporciones diferentes a lo establecido podría suponer problemas de almacenamiento: una lata muy alta además de ser más inestable y susceptible a deformación podría no caber en un frigorífico pequeño mientras que una lata muy gorda podría desperdiciar mucho espacio al no poder poner tantas latas a su alrededor o incluso ser incómodo al ocupar mucho espacio en la mesa.

Si se analiza, para un volumen fijo, la superficie necesaria para fabricar la lata cilíndrica en función de la relación altura/radio de la base, se obtiene la siguiente evolución:

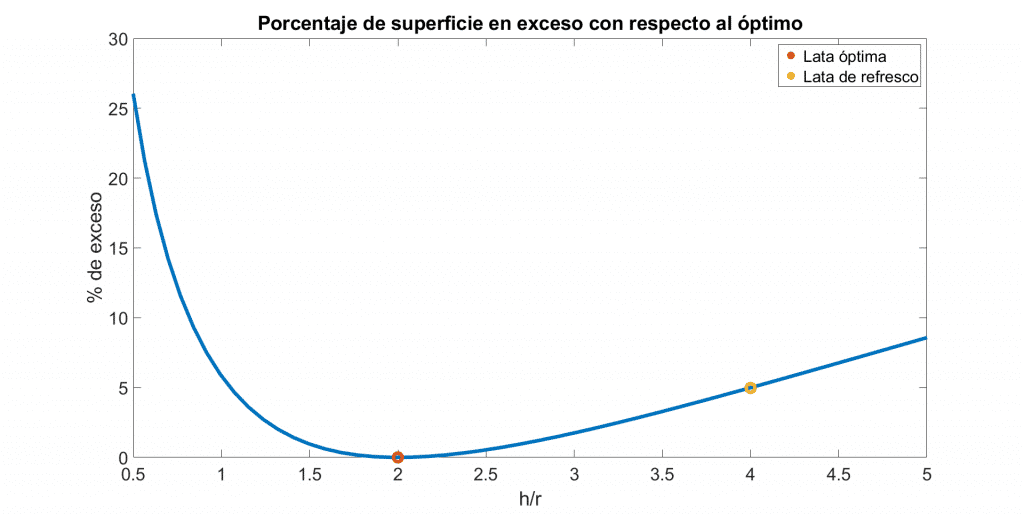
Situando en \(\dfrac{h}{r}=2\) la proporción óptima y en \(\dfrac{h}{r} \approx 4\) la relación que se da en una lata normal de 330ml, se ve cómo hay un exceso de superficie pero es bastante reducido, alrededor de un 5%. Por lo tanto, tiene más peso en la venta del producto que la lata sea cómoda y luzca bien.