Introducción
Está circulando por internet estos días el acertijo físico-matemático que se presenta en la foto anterior.
Tenemos 2 recipientes, ambos con la misma cantidad de agua y a la misma altura. De hecho, son idénticos, pero volteados. Es decir, el recipiente X tiene la parte ancha en la parte superior, y el recipiente Y tiene la parte ancha abajo.
Si abrimos el grifo a la vez, ¿Qué recipiente se vacía primero?
Teoría y matemática
Antes de poder dar una respuesta hay que comprender qué influye en la velocidad de salida del líquido.
La fórmula que describe la velocidad de salida (ideal, es decir, sin tener en cuenta la viscosidad, rozamiento etc) de un líquido por un orificio en un recipiente se deriva del principio de Bernoulli, el cuál puede derivarse de las ecuaciones diferenciales de cantidad de movimiento como se desarrolla en el artículo enlazado.
\( \boxed{\underbrace{\frac{1}{2} \rho v^{2}}_{Dinamica} + \underbrace{P}_{Estatica} + \underbrace{\rho g h}_{Hidrostatica} = \underbrace{P_{o}}_{Total}}\)
Es decir, que el valor de cada una de esas variables en cualquier punto del fluido es el mismo. Tomemos como ejemplo el siguiente recipiente:
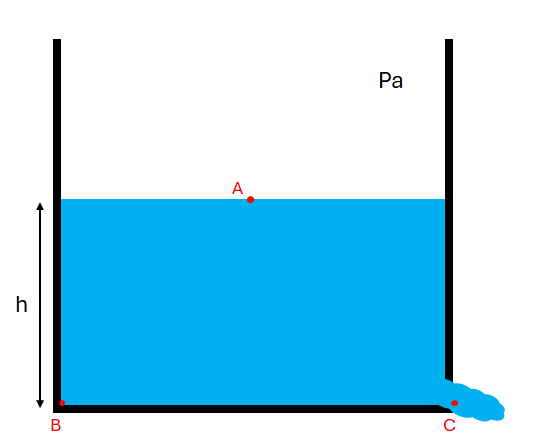
La ecuación de Bernoulli nos dice que el valor de la contante en cada uno de los puntos es el mismo, Es decir:
- \( \frac{1}{2} \rho v_{A}^{2} + P_{A} + \rho g h_{A} =P_{o}\)
- \( \frac{1}{2} \rho v_{B}^{2} + P_{B} + \rho g h_{B} =P_{o}\)
- \( \frac{1}{2} \rho v_{C}^{2} + P_{C} + \rho g h_{C} =P_{o}\)
Teniendo en cuenta que los valores de altura, velocidad y presión los tomamos como relativos, es decir, considerando que el recipiente está en reposo (velocidad de referencia 0), la presión exterior es la presión atmosférica, y que tomamos la altura de la base del recipiente como 0, las ecuaciones, despejando los términos nulos, nos quedarían:
- \( P_{a} + \rho g h =P_{o}\)
- \( P_{B} =P_{o}\)
- \( \frac{1}{2} \rho v_{C}^{2} + P_{a} =P_{o}\)
De dicha relación sacamos 2 conclusiones:
- La presión total o estática es igual a la presión en el fondo del recipiente en reposo
- Igualando la primera y segunda ecuación, podemos deducir la fórmula de la velocidad de salida como:
\( \rho g h = \frac{1}{2} \rho v^{2} \rightarrow v = \sqrt{2gh}\)
Por lo tanto, si tenemos un recipiente con líquido a una altura h, y abrimos un agujero en la parte inferior, la velocidad de salida viene dada exclusivamente por el valor de la gravedad (constante) y la altura del líquido. Es decir, la forma del recipiente no afecta, así como tampoco afecta la densidad del fluido.
¿Significa eso que la solución al problema es que ambos recipientes se vacían a la vez? Porque su altura es la misma
Pues NO. A medida que el recipiente se vacía, la altura del agua va disminuyendo a un cierto ritmo. Un cierto ritmo que depende a su vez del volumen de agua, es decir, podríamos definir la variable altura del líquido como:
\(h = h(V(t)) = h(t)\)
Resolución sencilla
Pongamos que queremos ver la evolución de la altura del agua en un ejemplo sencillo de un recipiente rectangular como el del esquema.
Digamos que la base tiene una superficie \(S\), y parte de una altura inicial \(h_{o}\). Es decir, que el volumen del líquido viene dado por \(V(t) = S \cdot h(t)\). Hay un agujero de salida de área \(A\).
El flujo se define como la cantidad de agua por unidad de tiempo que pasa por una sección. Siendo \(A\) el área de salida y \(v(t)\) la velocidad de salida, para poder ver la evolución temporal, podemos analizar la siguiente ecuación diferencial:
\(\dfrac{d V(t)}{dt} = S \dfrac{d h(t)}{dt} = -A \cdot v(t) = -A \sqrt{2gh(t)}\)
\(\dfrac{d h(t)}{dt} = -\dfrac{A}{S} \sqrt{2gh(t)}\)
Es decir, que agrupando términos:
\(\dfrac{dh}{\sqrt{h}} = – \dfrac{A}{S} \sqrt{2g} dt\)
\(\displaystyle \int_{h_{o}}^{h(t)} h^{-1/2} dh = – \dfrac{A}{S} \sqrt{2g} \int_{0}^{t} dt\)
\(\displaystyle \boxed{h(t) = \left ( \sqrt{h_{o}} – \dfrac{A}{2S} \sqrt{2g} \ t \right )^{2}}\)
Dicha ecuación sólo es válida hasta que \(h(t) = 0\), y se puede comprobar que \(h(0) = h_{o}\)
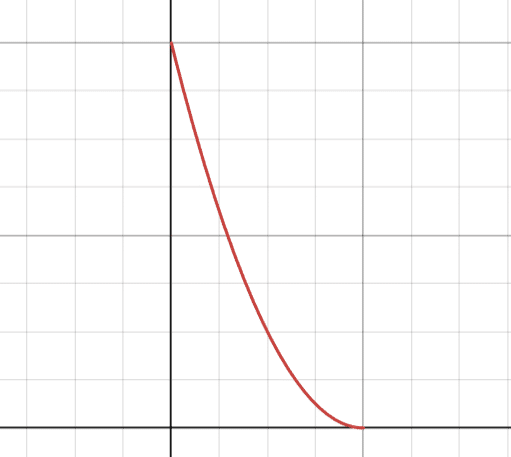
Si representásemos la función gráficamente, veríamos que tiene forma de parábola tal que:
\(y(x) = (a – b x)^{2}\)
Resolución recipiente complejo
Lo que hemos visto hasta ahora es que la velocidad de salida del fluido ideal depende exclusivamente de la altura del líquido (h(t)), la aceleración gravitatoria (g) y el área del orificio (A) según la siguiente ecuación:
\(\boxed{\dfrac{d V(t)}{dt} = -A \sqrt{2gh(t)}}\)
En el caso anterior fue fácil obtener la ecuación diferencial al poder expresar la diferencia de volumen como
\(\dfrac{d V(t)}{dt} = S \dfrac{dh(t)}{dt}\)
No obstante, para los recipientes del enunciado, debemos de establecer una relación entre ambas variables.
Desarrollo con ecuación del volumen de un tronco de cono
Para obtener el volumen de un cuerpo de revolución, guiándonos por https://ingenieriabasica.es/demostracion-formulas-de-area-y-volumen/, podemos definirlo por secciones, es decir:
\(\displaystyle V(h) \int_{0}^{h} \pi \rho(y)^{2} dy\)
Siendo \(\rho(y)\) el radio de la sección que en todo momento depende de la altura.
En el caso Y, es decir, un tronco cónico de base inferior R y base superior r (con R > r), la fórmula de la sección con la altura vendría dada como:
\(\rho(y) = R – \dfrac{R – r}{H} y = R – k y\)
Por lo tanto, sustituyendo en la fórmula del volumen:
\(\displaystyle V(h) \int_{0}^{h} \pi (R – k y)^{2} dy = \pi \int_{0}^{h} \left ( R^{2} + k^{2}y^{2} – 2Rky \right )\)
Podríamos integrar para sacar el volumen y seguir haciendo análisis.
En cualquier caso, lo que nosotros queremos saber es la evolución \(\dfrac{dh(t)}{dt}\) para ver, en función de la orientación del recipiente, cuál se vacía primero.
Por lo tanto, podemos hacer el siguiente truco. Sabemos que la evolución del volumen con respecto a la altura es la siguiente:
\(\dfrac{dV(h)}{dh} = \pi \rho(h)^{2} = \pi (R – k h)^{2}\)
Y que la evolución del volumen con respecto al tiempo es la siguiente:
\(\dfrac{d V(t)}{dt} = -A \sqrt{2gh(t)}\)
Por lo tanto, si combinamos las expresiones para encontrar la evolución de la altura con respecto al tiempo:
\(\dfrac{dh}{dt} = \dfrac{dh}{dV} \dfrac{dV}{dt} = – \dfrac{A \sqrt{2gh}}{\pi (R – k h)^{2}}\)
Aquí la resolución de la ecuación se complica más al tener la variable h también en el denominador. No obstante, no estamos interesados en obtener la evolución temporal de la altura con respecto al tiempo de cada recipiente (que se podría obtener rápidamente con cualquier integrador numérico), sino comparar ambas evoluciones y ver cuál es más rápida.
Definiendo:
\(K = \dfrac{A \sqrt{2g}}{\pi}\)
La evolución nos quedaría, para cada caso:
\(\dfrac{dh_{Y}}{dt} = – \dfrac{K \sqrt{h}}{(R – k h)^{2}} = – \dfrac{K \sqrt{h}}{(\rho_{Y}(h))^{2}}\)
\(\dfrac{dh_{X}}{dt} = – \dfrac{K \sqrt{h}}{(r +k h)^{2}} = – \dfrac{K \sqrt{h}}{(\rho_{X}(h))^{2}}\)
Es decir, que la velocidad del vaciado es proporcional la raíz de la altura actual, e inversamente proporcional al área transversal.
Inicialmente, la altura de ambos recipientes es la misma, pero el área transversal del tanque Y es menor, por lo que su altura disminuye más rápidamente al inicio. Siendo el volumen de líquido el mismo en ambos recipientes, el tanque X descarga más líquido al mantener más altura.
Además, en todo momento (excepto en t=0), para un mismo volumen V, el recipiente X tendrá siempre más altura que el recipiente Y al tener un área transversal menor en la base. Eso garantiza que, a igualdad de volumen en el tanque, el recipiente X descargará más rápido al tener más altura.
Eso también implica que, a misma altura del líquido, en el recipiente X habrá menos volumen de líquido (excepto en t=0). Por lo tanto, se garantiza que una vez que se abre la salida, el recipiente X toma ventaja y la mantiene durante el vaciado.
Por dichos motivos, queda demostrado que el recipiente X se vacía antes
Desarrollo con energía potencial y cinética
Si calculásemos el centro de masas de cada uno de los fluidos con el volumen al máximo, es fácil observar que la altura del centro del tanque X es mayor que la del tanque Y.
Eso implica, por lo tanto, una mayor energía cinética, que, para un mismo orificio de salida, se traduce en evacuar mayor cantidad de agua por unidad de tiempo.
Se podría hacer un análisis comparativo similar con números y se llegaría a la misma conclusión. Quise comentar esta alternativa porque siempre es interesante ver cómo diferentes caminos llevan al mismo resultado. Si tienes curiosidad, ¿Por qué no pruebas a hacer los cálculos? 😉
Caso alternativo: tanques simétricos

En este caso, ¿Cuál se vacía primero?
No he hecho ningún análisis numérico, pero tirando por el desarrollo de la energía potencial, ambos presentan la misma, por lo que el tiempo de vaciado debería ser el mismo.
El siguiente vídeo hace un desarrollo numérico y le sale diferente, pero desconfío del resultado:
¿Os atrevéis a hacer los números? Os leo 🙂