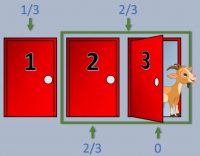
Al igual que en España y el resto de países, en EEUU realizan una serie de exámenes o pruebas que, sumado a la nota media del expediente, permiten a los estudiantes competir para ingresar en las universidades. Uno de estos exámenes es el SAT (Scholastic Assessment Test), que tiene preguntas de comprensión lectora y matemáticas.
Dicho examen se estructura con una serie de preguntas tipo test que deben responderse en muy poco tiempo (menos de 1 minuto por pregunta), y el objetivo es valorar la rapidez mental y la velocidad con la que un estudiante puede razonar para elegir la respuesta correcta.
No obstante, el examen de 1982 pasó a la historia porque hubo una pregunta que todo el mundo falló. Y fue así porque la pregunta escondía una paradoja tan interesante que ni los propios examinadores se dieron cuenta y no incluyeron la respuesta correcta como solución.
El enunciado del problema imposible
A continuación se presenta el enunciado:
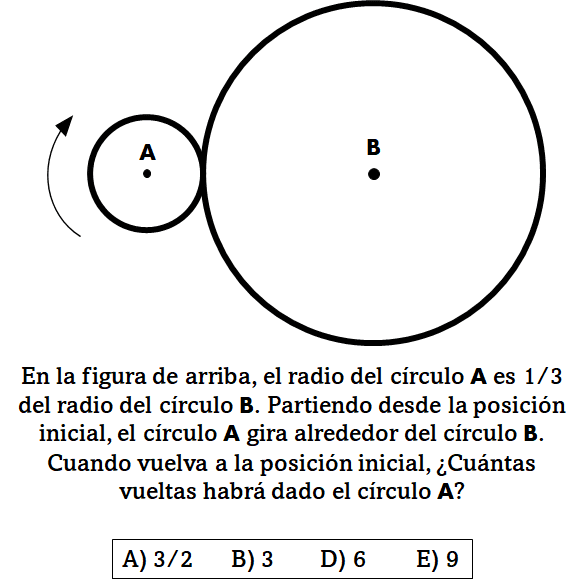
Recordemos que el estudiante tendría menos de 1 minuto para dar con la respuesta correcta. El planteamiento para hallar la solución no tomaría mucho más tiempo, y sería el siguiente:
- Me piden el número de revoluciones de la circunferencia A para que vuelva a la posición inicial.
- Dicho número de revoluciones debe ser tal que la circunferencia A recorra una cierta longitud \(L\), la cuál es precisamente el perímetro de la circunferencia B.
- El perímetro de la circunferencia B es \(L = 2 \pi R\) con \(R=3r\), siendo \(r\) el radio de la circunferencia A.
- En 1 revolución de la circunferencia A, se recorre una distancia \(l = 2\pi r\)
- Por lo tanto, hay que resolver la ecuación:
- \(x\cdot l = L \rightarrow x \cdot (2\pi r) = 2 \pi \cdot (3 r)\)
- \(x \cdot (2\pi r) =(2\pi r) \cdot 3 \rightarrow \boxed{x = 3}\)
Por lo tanto, según el razonamiento, la respuesta sería 3, que es lo que la mayoría de estudiantes marcó y la que los examinadores pensaban que era la respuesta correcta. No obstante, unos pocos estudiantes indicaron que la respuesta correcta no estaba entre las opciones y pusieron quejas al respecto. Al final se verificó que los estudiantes estaban en lo cierto y anularon la pregunta.
La solución correcta y el razonamiento
Vamos a hacer una prueba experimental para comprobar de manera empírica cuál es el número de vueltas. Recortamos 2 circunferencias manteniendo el ratio de radios y hacemos que la pequeña rote alrededor de la grande. Obtendremos el siguiente resultado:
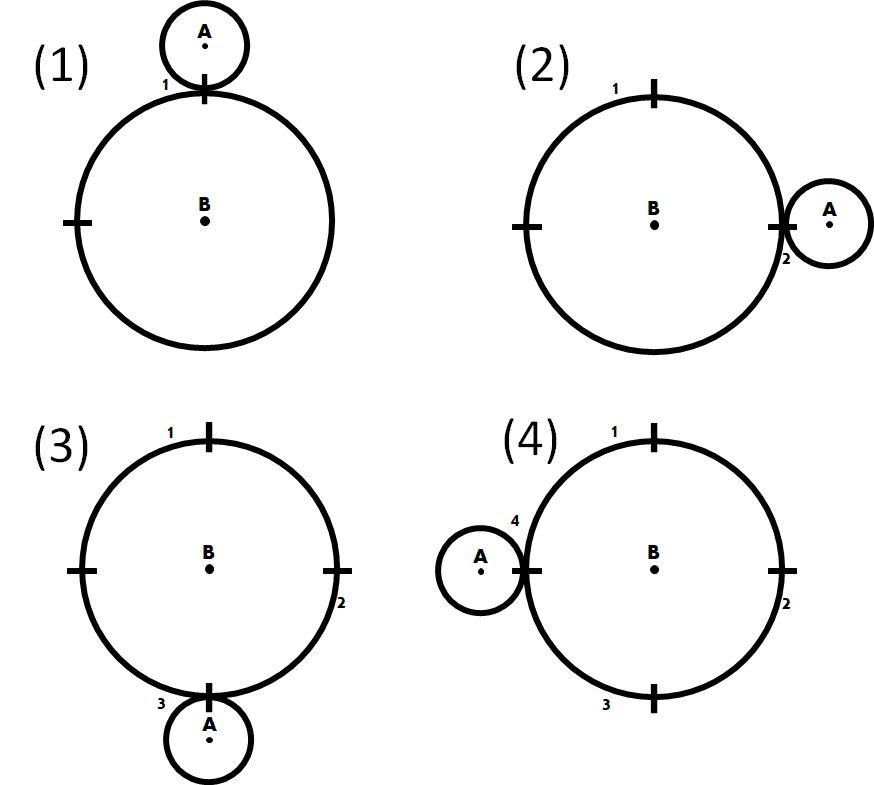
Es decir, que realmente serían necesarias 4 vueltas y no 3 como pensábamos inicialmente. Si seguimos el procedimiento definido en nuestro planteamiento mental de convertir el perímetro de la circunferencia grande en una recta y hacer girar la pequeña sobre ella hasta recorrerlo por completo, obtendríamos el siguiente resultado:
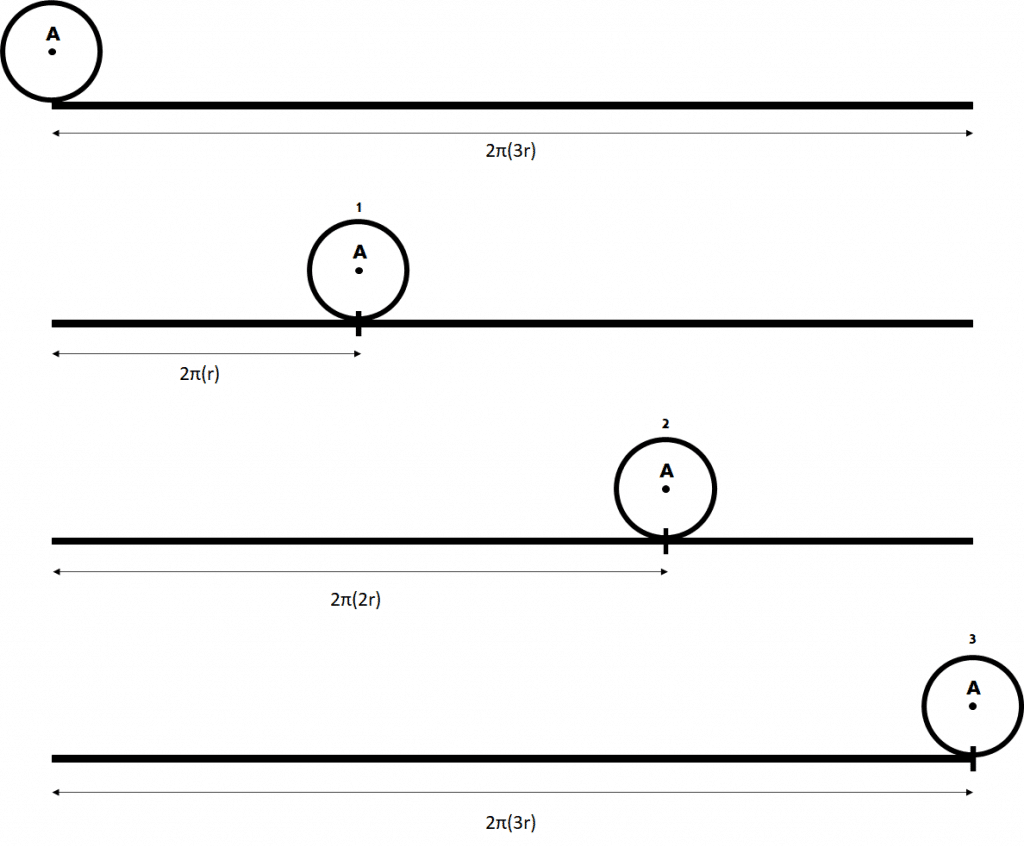
Entonces… ¿Qué está pasando? ¿Por qué cuando la circunferencia rota sobre otra, debe rotar una vuelta más para volver al punto inicial, pero si la superficie sobre la que se rota fuese recta, no haría falta ese giro extra?
La respuesta está en la distancia que recorre el centro. Si miramos la siguiente imagen, nos quedará más claro:
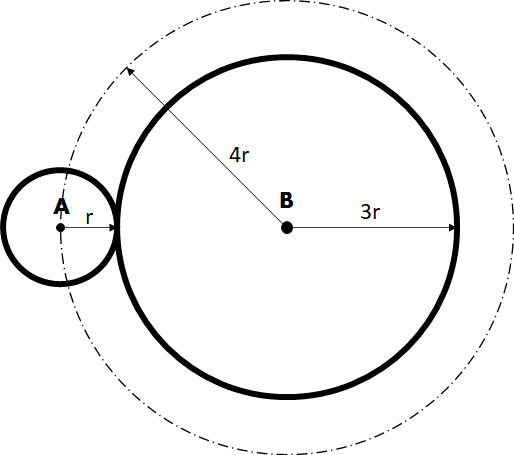
Es decir, que el centro de la circunferencia A debería de recorrer no una distancia de \(L = 2 \pi (3r)\) sino de \(L = 2 \pi (4r)\). El problema en el planteamiento inicial del problema es a la hora de aplicar la fórmula. Cuando una circunferencia rueda sin deslizamiento una vuelta completa, es el centro de dicha circunferencia lo que se desplaza una distancia \(2 \pi r\). Cuando la superficie que se recorre es recta, no hay problema porque la distancia que recorre el centro es la misma que se avanza sobre la superficie, pero no es nuestro caso. Esto se puede ver gráficamente en la siguiente imagen:
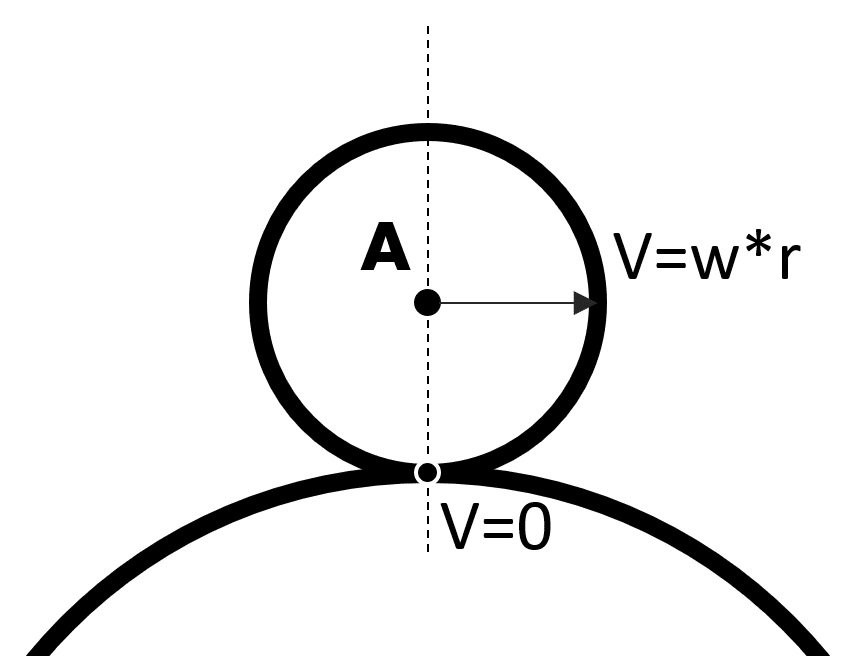
Por lo tanto, y calculando el número de vueltas correcto en base a la distancia que recorre el centro, el resultado sería 4.
Para que la velocidad de avance sobre la superficie curva fuese la misma que la del centro, la circunferencia grande debería de estar rotando en sentido contrario de forma que la velocidad relativa con respecto al centro fuese -V, como pasa en los engranajes. Es decir, si en el dibujo inicial no hubiesen circunferencias sino que fuesen ruedas dentadas de forma que el engranaje B gira libremente, serían necesarias 3 vueltas del engranaje A para volver a la posición inicial.
Si te ha gustado esta paradoja acerca de circunferencias y radios, te aconsejo que leas La paradoja de la cuerda y el conejo.