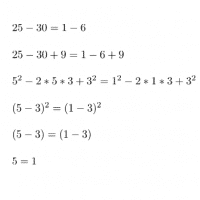Los amantes de las matemáticas recreativas se habrán encontrado este problema alguna vez:
\(¿0.\hat{9} = 1?\)
Es decir; ¿Es 0.99999 (0.9 periódico) igual al número natural 1? No tiene ningún sentido que un número decimal periódico sea equivalente a un número natural; pertenecen a diferentes categorías.
No obstante, sorprendentemente, la equivalencia se cumple. En este artículo se van a mostrar varios ejemplos ingeniosos para mostrar dicha equivalencia, eliminando cualquier duda.
Demostración por fracción de que 0.999… es 1
Dividiendo 1 entre 3 obtenemos el número decimal periódico 0.333… Si multiplicamos a ambos lados de la igualdad por 3, sin duda alguna llegamos al resultado buscado.
\(\dfrac{1}{3} = 0.\hat{3}\)
\(3 \cdot \dfrac{1}{3} = 3 \cdot 0.\hat{3}\)
\(\boxed{1 = 0.\hat{9}}\)
Demostración pasando decimal periódico puro a fracción
Si intentamos convertir 0.999… a fracción por el método descrito en este artículo (¡y que recomiendo encarecidamente echar un ojo puesto que es la forma más eficiente sin tener que recordar pasos absurdos!) obtendremos como solución el 1:
\(x = 0.\hat{9}\)
\(10x = 9.\hat{9}\)
\(10x – x = 9.\hat{9} – 0.\hat{9}\)
\(9x = 9\)
\(x = \dfrac{9}{9} = \boxed{1 = 0.\hat{9}}\)
Demostración por descomposición en fracciones de potencias de 10
Una demostración más avanzada que involucra una suma infinita consiste en descomponer el 0.999… en una suma infinita de fracciones de potencias de 10:
\(0.\hat{9} = 0.999\dots = 0.9 + 0.09 + 0.009 + \dots =\)
\(= \dfrac{9}{10} + \dfrac{9}{100} + \dfrac{9}{1000} \dots = \dfrac{9}{10^{1}} + \dfrac{9}{10^{2}} + \dfrac{9}{10^{3}} \dots = \)
\(\displaystyle = \dfrac{9}{10} \cdot \sum_{n=0}^{\infty} \left ( \dfrac{1}{10}\right )^{n} \)
Recordemos el desarrollo de la serie geométrica:
\({\displaystyle \sum _{k=0}^{\infty }r^{k}={\frac {1}{1-r}}}\)
Por lo tanto, tenemos que:
\(\displaystyle \dfrac{9}{10} \cdot \sum_{n=0}^{\infty} \left ( \dfrac{1}{10}\right )^{n} = \dfrac{9/10}{1-1/10} = \dfrac{9/10}{9/10} = \boxed{1 = 0.\hat{9}}\)
Conclusión
Es posible que haya tantas demostraciones matemáticas de esta equivalencia como formas de demostrar el Teorema de Pitágoras. Unas más complejas que otras, empleando herramientas más o menos potentes de las matemáticas, pero en definitiva dando el mismo resultado; 0.9 periódico es igual a 1.
Si te gusta este tipo de artículo no dudes en visitar la categoría de Juegos Matemáticos.