En las redes sociales, de vez en cuando, se hace “viral” algún truco matemático cuyo resultado se escapa a la lógica. Y es que hay trucos de todos los tipos; hacer que 2×2 sea igual a 5, hacer que independientemente del número que elijas siempre obtengas el mismo resultado, o demostrar que 1+1=3.
En este artículo voy a exponer un par de demostraciones matemáticas inválidas y me gustaría que, antes de ver la solución, intentéis reflexionar y daros cuenta en qué parte de la demostración he cometido un error gravísimo (PROHIBIDO) en matemáticas que hace que mi resultado no sea coherente.
Demostración de que 5=1
Voy a comenzar con un ejemplo numérico de cómo obtener un resultado incoherente:
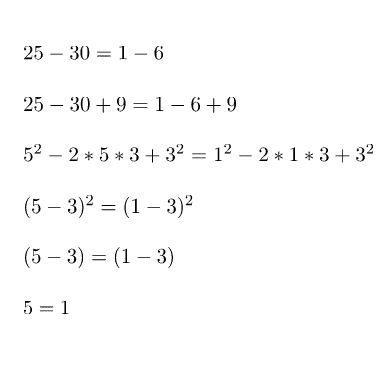
Qué tal, ¿Tenéis el culo torcido? No tiene ningún sentido esta solución pero… ¿Os habéis dado cuenta de por qué? ¿En qué parte violo alguna ley básica de álgebra para obtener el resultado que yo quiero? Si no eres capaz de verlo, fíjate en la siguiente demostración.
Demostración de que a=b partiendo de a≠b
Esta es una generalización del caso anterior empleando letras en vez de números (Fundamental para demostrar algo matemáticamente). Tras dar valores arbitrarios a nuestras constantes a y b, usando este desarrollo podemos sacar cualquier demostración como la anterior para llegar a a=b (0=5, 5=22, etc…). Voy a usar letras para que veáis cuál es el proceso e identifiquéis el fallo.
Iniciamos planteando la ecuación:
\(a^{2}-2*a*c=b^{2}-2*b*c\)Que, para ser válida, debemos de elegir un valor de c de forma que:
\(a^{2}-b^{2}+2*c*(b-a)=0 \rightarrow c=\frac{a^{2}-b^{2}}{2*(a-b)}\)Una vez obtenido el valor de c, lo dejamos indicado y seguimos operando:
\(a^{2}-2*a*c=b^{2}-2*b*c\) \(a^{2}-2*a*c + c^{2} = b^{2} – 2*b*c + c^{2}\) \((a-c)^{2}=(b-c)^{2}\) \((a-c)=(b-c)\) \(a=b\)Observamos que no tiene ningún sentido, ya que la ecuación se cumple para cualquier valor que tomemos de a y b (Aunque sean distintos) pero tras desarrollar los cálculos llegamos a que para que se cumpla, a debe ser igual a b. ¿Qué está sucediendo?

Si vamos siguiendo los cálculos, hasta la antepenúltima línea todo es correcto. Sin embargo, el fallo enorme viene cuando hacemos la raíz cuadrada y dejamos los paréntesis tal cual. De esta forma, estamos “forzando” que ambos términos sean positivos, y la única solución que obtenemos para que la ecuación inicial sea válida es la de a=b. Sin embargo, extendiendo un poco más nuestro razonamiento, observamos que si a=b el valor de nuestra constante c tiende a infinito, dejando de ser un valor admisible. Antes de volvernos locos, vamos a analizar con rigor matemático esta ecuación.
Partiendo de una igualdad, llegamos a una solución cuyos valores no incluyen a los valores del planteamiento inicial. Es difícil de explicar, pero voy a calcular las soluciones correctamente para que lo veáis.
En primer lugar, vamos a matizar la definición de la constante c.
La constante c se define como:
- Para \(a \not = b \rightarrow c=\frac{a^{2}-b^{2}}{2*(a-b)}\)
- Para \(a = b \rightarrow c\) toma el valor de cualquier número real.
Este último matiz es válido porque si a=b, para cualquier valor real de c se cumple la igualdad ya que introduciendo a=b en la ecuación inicial al instante se obtiene 0=0.
Una vez definido los valores de c, desarrollamos las cuentas de la misma forma, hasta que llegamos a:
\((a-c)^{2}=(b-c)^{2}\)Para quitarnos el cuadrado en ambos lados correctamente, debemos de colocar valores absolutos, ya que puede que tengamos que evitar igualar un término positivo con otro negativo.
\(|a – c| = |b – c|\)Tenemos 2 soluciones:
- \(a-c = b-c \rightarrow a=b\)
- \(a-c = -(b-c) \rightarrow a= 2c – b\)
Tomando los valores de la demostración de 5=1, inicialmente hemos elegido a=5, b=1 y c=3.
Como \(a \not = b \) , debemos usar la segunda solución, de forma que \(a=2c-b \rightarrow 5=6-1 = 5 \) ✅
Por lo tanto, el planteamiento correcto debería de haber sido el siguiente:
\((5-3)^{2} = (1-3)^{2}\) \((5-3) = -(1-3)\)\(2=2\) ✅
Demostración de que 2=1
Vamos a obtener otra solución incoherente, pero esta vez no empleando el truquillo de las raíces cuadradas.
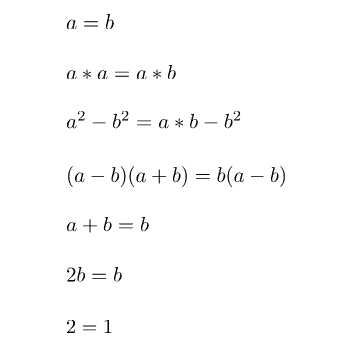
Esta demostración es mucho menos sutil que la anterior ya que todo el tiempo se ve como en cualquier momento restando términos se llega a a=b=0. Sin embargo, al igual que en el primer caso y como si de un truco de magia se tratase, hay que respetar todos los cálculos intermedios y observar el resultado final.
Como era de esperar, la solución no es coherente. Pero… ¿Dónde está el fallo?
Dividir por 0. Si, en las matemáticas, como sabréis está prohibido dividir por 0. O, mejor dicho, está prohibido si no eres consciente de lo que estás haciendo.
En el momento que decimos que a=b pero, sin embargo, en una línea escribimos (a-b)*k , ya estamos diciendo que el valor de k puede ser cualquiera que la ecuación sigue siendo válida.
Esto se debe a que 0*50 = 0*2. El 0 lo niega todo (Menos el infinito, claro), y no importa lo que multipliquemos por 0 que el resultado va a ser siempre el mismo. Sin embargo, yo no puedo coger y dividir por 0 en ambos lados y quedarme con 50=2, ya que matemáticamente no es correcto.
Lo que quiero decir es que multiplicar por 0 o infinito cambia por completo el valor afectado, de forma que utilizar estos valores a la ligera para después dividir es matemáticamente incorrecto, y es por ello que se llegan a soluciones absurdas si no se hace con cuidado.
Un claro ejemplo es a la hora de resolver una ecuación. Supongamos que yo tengo la ecuación \(5x^{2}-2x=0\) y quiero hallar qué valor de x hace que cumpla la ecuación.
Un novatillo podría coger y decir:
\(5x^{2}-2x=0\) \(5x-2=0\) \(x=\frac{2}{5}\)Y que, comprobando, vemos que
\(5*\frac{4}{25} – 2*\frac{2}{5} = \frac{4}{5}- \frac{4}{5} =0\)Es decir, que nuestra solución es correcta. Pero claramente hemos cometido un error; al dividir entre x hemos forzado que no sea posible obtener un valor de x=0. Por lo tanto, esa solución la hemos descartado y por eso no nos aparece. Sin embargo, es un error importante ya que x=0 es una de las soluciones de dicha ecuación, y podría suponer la única solución admisible (Por ejemplo, que en el cálculo de una masa o un tiempo nos salga como solución única un valor negativo (físicamente no posible), y no nos percatemos de otra solución admisible que no nos aparece porque al dividir en algún momento la hemos descartado sin querer)
Conclusión
Internet está plagado de trucos como estos, e intentar recopilarlos todos en un artículo sería imposible. Desde demostraciones de \(\pi = e = 3\), a \(1+1=7\)…
Lo que todos tienen en común es que o bien hacen una raíz cuadrada y ocultan la solución negativa, o dividen entre 0 (Siendo este último lo más típico).
Como conclusión he de decir que, si bien no hay que estar constantemente tomando valores absolutos para las raíces cuadradas y no dividiendo por miedo a hacerlo por 0, todo se reduce a saber qué está haciendo uno en todo momento. No nos vamos a encontrar una ecuación rocambolesca como las que he planteado (En cuyo desarrollo intermedio si se pasan todos los términos a un lado se va al carajo el truquillo), pero sí que nos podemos tender una trampa a nosotros mismo a la hora de calcular una solución como en el ejemplo de \(5x^{2}-2x=0\) o principalmente al resolver sistemas de ecuaciones no lineales, donde debemos de ir asumiendo/descartando ciertas soluciones para poder continuar el desarrollo.
Si algo huele mal, lo mejor es dar marcha atrás y ver en qué punto deja de tener sentido el desarrollo.