El teorema de Pitágoras, las fórmulas básicas de área y volumen y la mítica ecuación para resolver ecuaciones de segundo grado es lo único que la mayoría de la gente que no ha estudiado una carrera técnica recuerda de las matemáticas de instituto.
El teorema de Pitágoras es uno de los teoremas más antiguos que se conoce y se debe su nombre a Pitágoras, quien demostró el siguiente teorema en el siglo VI a.C.:
En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Siendo la hipotenusa el lado de mayor longitud y los catetos los otros lados
\(a^{2}+b^{2}=c^{2}\)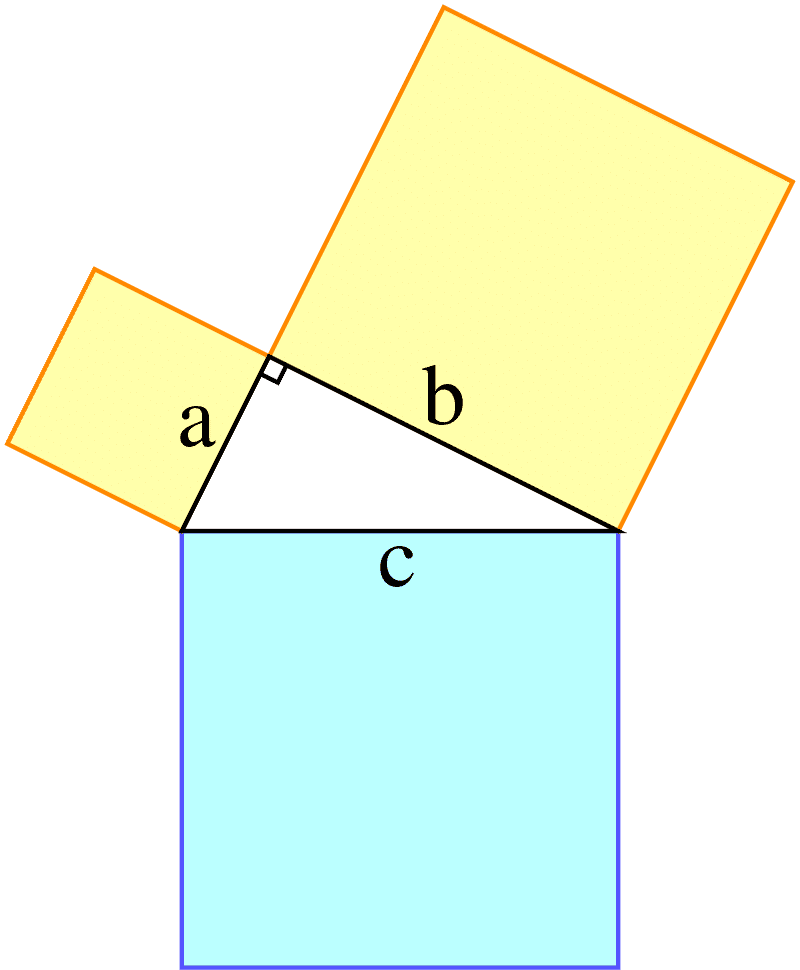
Y digo demostró porque el empleo de dicha relación en los triángulos en construcciones se remonta a tiempos más antiguos. Sin embargo, no hay documentos anteriores a Pitágoras en los que se demostrara dicho teorema.
Además de ser el teorema más conocido, es de los que más demostraciones tiene (Probablemente el que más). Esto se debe en parte a que en la edad media se exigía una nueva demostración del teorema de Pitágoras para alcanzar el grado de «Magíster matheseos».
Como he dicho hay infinidad de demostraciones. En este artículo voy a demostrarlo por dos formas: La algebraica ya que es la más sencilla e intuitiva, y la geométrica, que es algo más clásica y que se supone que empleó Pitágoras en su demostración.
Demostración algebraica
Esta es la demostración más intuitiva y más fácil de explicar de todas las existentes.
Para empezar partiremos de un cuadrado de lado (a+b) compuesto por 4 triángulos rectángulos (De lados a,b y c) y un cuadrado de lado c
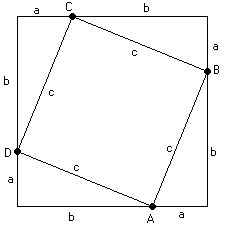
Vamos a demostrar que \(a^{2}+b^{2}=c^{2}\) independientemente de los valores a,b y c tal y como asegura el teorema.
Vamos a hacer un recuento de áreas:
- El cuadrado grande tiene un área igual a \((a+b)^{2}\)
- Cada triángulo tiene un área de \(\frac{a*b}{2}\), lo que hacen un área total los 4 triángulos de \(2*a*b\)
- El cuadrado interior tiene un área de \(c^{2}\)
¡No queda nada!
Entonces se tiene que el área del cuadrado grande es igual a la suma del área de los triángulos y el cuadrado pequeño. Lo que matemáticamente se traduce a una ecuación:
\((a+b)^{2}=2*a*b+c^{2}\)Desarrollando el binomio al cuadrado
\((a+b)^{2}=a^{2}+b^{2}+2*a*b=2*a*b+c^{2}\)Y finalmente restando el término 2ab nos queda:
\(a^{2}+b^{2}=c^{2}\)Quedando demostrado de una forma muy bella y elegante el famosísimo teorema de Pitágoras
Aquí puedes verlo gráficamente
Demostración geométrica
Como demostración geométrica vamos a emplear la que en teoría empleó Pitágoras y que es probablemente la más intuitiva de las geométricas. Para ello se basó en el concepto de semejanza de triángulos.
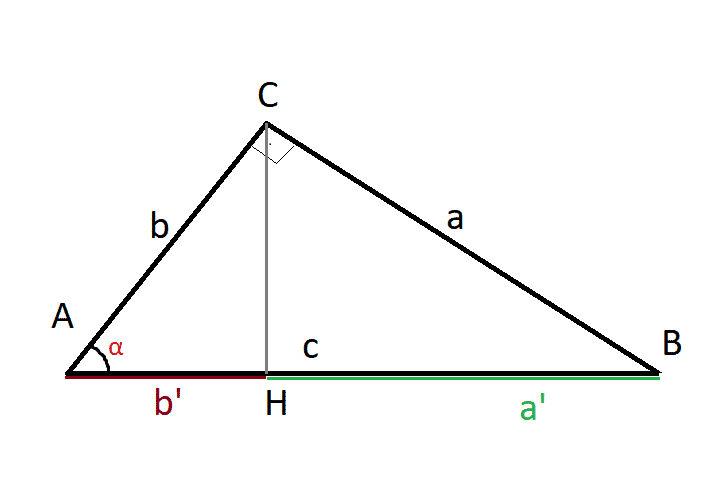
Partiremos del triángulo de la figura con los puntos así marcados. La altura del triángulo la marca el segmento CH y lo divide en dos triángulos más pequeños, uno de base b‘ y otro de base a’. a’ y b’ son las proyecciones sobre la base del triángulo de a y b respectivamente.
Los tres triángulos ABC, AHC Y BHC son semejantes. Es decir, la proporción entre los lados y los ángulos es idéntica. Son el mismo triángulo pero en distintas escalas.
De ello se extrae la siguiente equivalencia (b sería equivalente a decir c’):
\(\frac{b’}{b}=\frac{b}{c}\)¿No lo ves? Bueno, para ello he pintado el ángulo \(\alpha\)
No vale emplear funciones para una demostración geométrica, pero para que sea intuitiva la relación de semejanza voy a hacer una equivalencia:
\(b’=b*cos(\alpha)\) \(b=c*cos(\alpha)\) \(cos(\alpha)=\frac{b’}{b}=\frac{b}{c}\)Con lo cual se demuestra la equivalencia de semejanza.
Aplicando lo mismo para a y a’ y colocando las fracciones convenientemente llegamos a:
\(\frac{b}{b’}=\frac{c}{b} \) \( \frac{a}{a’}=\frac{c}{a}\)Lo cual nos dice que
\(a^{2}=a’*c\) \(b^{2}=b’*c\)Y de esta forma, \( a^{2} + b^{2}=a’c+ b’c=c\left(a’+b’\right) \)
Pero como a’+b’ suman c, se demuestra que \( a^{2} +b^{2}= c^{2} \) , que se demuestra visualmente de la siguiente forma:
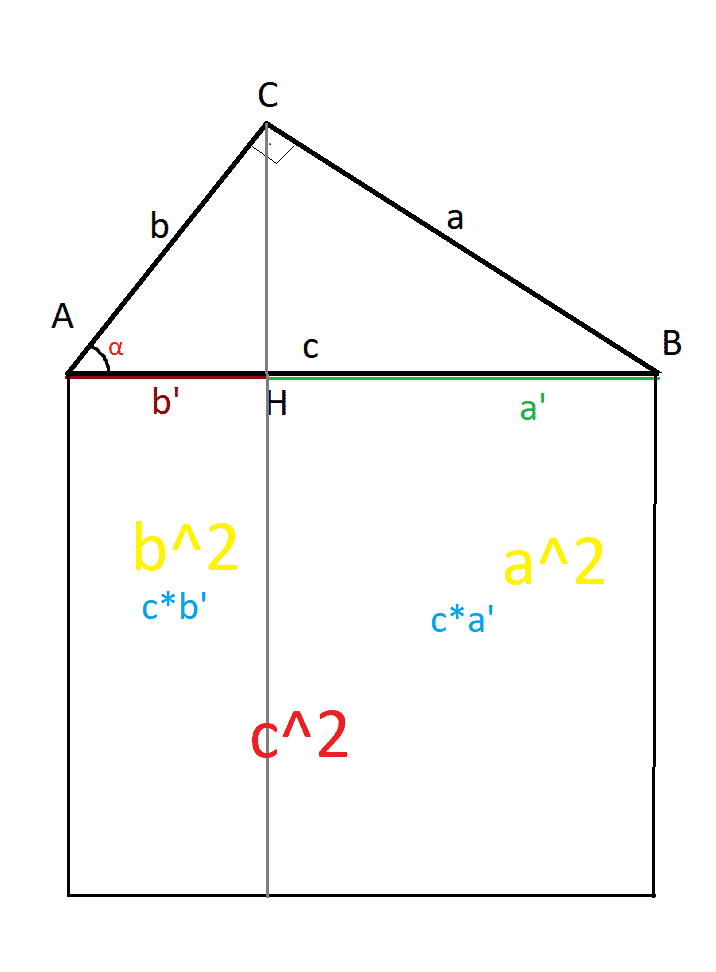




Conocía el teorema pero jamás supe por qué se cumplía. Buen artículo crack
:))
wow, sigo sin entender
Que la suma de cateto al cuadrado más cateto al cuadrado es igual a la hipotenusa al cuyadrado, la hipotenusa es la parte larga del triangulo y los catetos las partes largas
cateto las partes cortas (me he equivocado xd)
cateto las partes cortas (me he equivocado xd)
yo tampoco entiendo. Hace 55 años me llevé matemática por culpa de este teorema … Me rindo!!!
Falta demostrar por que la figura interior es un cuadrado.
Buena observación pero no haría falta porque date cuenta de que todos los triángulos rectángulos son idénticos, es decir que se forma una figura geométrica por medio de 4 segmentos de igual longitud, y que además su distribución es simétrica. Por lo tanto la figura es un cuadrado.
Si fuese un rombo, al tu rotar el cuadrado principal y a su vez rotar todos los rectángulos (que son indénticos) estarías obteniendo una figura interior (rombo por ejemplo) que varía su «forma» a medida que vas rotando el cuadrado principal. Y eso no cuadraría porque como te digo los triángulso rectángulos se distribuyen de manera uniforme y simétrica.
porque son las hipotenusas de los cuatro triangulos iguales
Gracias. Muy Bueno.
es claro que (siendo beta el ángulo entre los lados a y c en la fig de la demostración geométrica):
La hipotenusa «C» = b*cos(alpha)+ a*cos(beta)
además, cos(beta) = sen(alpha) [propiedades de los ángulos internos de un triángulo recto: suma 180 º]
entonces c = b*cos(alpha)+a*sen(alpha)
y c²= ( b*cos(alpha)+a*sen(alpha))²
o sea = c² = (b*cos(alpha))² + (a*sen(alpha))² + 2*b*a* cos(alpha) * sen(alpha)
EL CASO ES QUE ESTA ECUACIÓN ES PERFÉCTAMENTE VÁLIDA . . . PERO. . . ¿COMO HAGO PARA SIMPLIFICARLA A LA MARAVILLOSA SÍNTESIS DE PITÁGORAS?
Buenas Enrique,
Intentas deducir el teorema de Pitagoras a raiz de 1 sola expresion que define el lado c. Y eso no es posible. Al final, como lo planteas llegas a expresar una igualdad tipo c = f(a,b,alpha)
Para poder llegar a c=f(a,b) tendrias que o fijar alpha, o tener otra ecuación en la que c=f'(a,b,alpha) y al comparar ambas ecuaciones puedas eliminar el alpha de forma que te quede c=f»(a,b)
Al final es lo que se hace en la demostración geométrica, se hace una división de 2 «ecuaciones» y se nos van las funciones trigonométricas.
De hecho, inicialmente partes de c= f(a,b,alpha,beta), y la ecuación de que alpha+beta = 180 es una ecuación que te permite eliminar beta. Necesitarías otra para eliminar alpha
Gracias por agregar mi applet de GeoGebra a tu página.