Las Leyes de Kepler es una de las cosas que nos aprendemos a fuego en el instituto junto al Teorema de Pitágoras o la Fórmula de ecuaciones de 2º grado y que, aunque la memoria no de tanto como para enunciarlas, en general todo el mundo recuerda que son 3.
En este artículo os refrescaré la memoria y no sólo las enunciaré, sino que aportaré una demostración matemática para cada una de ellas.
Las Leyes de Kepler
Las Leyes de Kepler fueron enunciadas, cómo no, por Johannes Kepler a principios del siglo XVII con el objetivo de sentar unas bases científicas acerca del movimiento de cuerpos alrededor del Sol.

Hasta esa fecha, numerosas teorías se habían ido enunciando. Desde el modelo puramente geocéntrico hasta modelos mixtos donde se introducían complejos artificios matemáticos que permitían validar la teoría que se pretendía enunciar de manera artificial (Un poco como hacen a día de hoy los terraplanistas para justificar las observaciones evidentes).
Kepler, con estas leyes basadas observaciones y mediciones (Tanto por él como por su maestro Tycho Brahe), intenta finalizar por completo el debate acerca de las órbitas enunciando unas leyes que en la actualidad se han demostrado que se cumplen a la perfección. Sin embargo, en esa época aún no existía el cálculo infinitesimal y Kepler aportó unas demostraciones matemáticas muy vagas y prácticamente geométricas.
Un par de años más tarde, nació el genio Isaac Newton y, junto con su Ley de Gravitación Universal y su desarrollo del cálculo infinitesimal, fue capaz de dar una demostración matemática, universal y elegante de las Leyes de Kepler.

Las Leyes
- Primera Ley: Todos los planetas se desplazan alrededor del Sol describiendo órbitas elípticas. El Sol se encuentra en uno de los focos de la elipse.
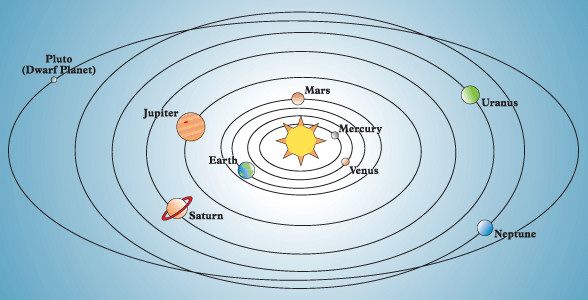
- Segunda Ley: El radiovector que une un planeta y el Sol barre áreas iguales en tiempos iguales. Por lo tanto, un planeta en su órbita irá más rápido en su perihelio y más lento en su afelio.
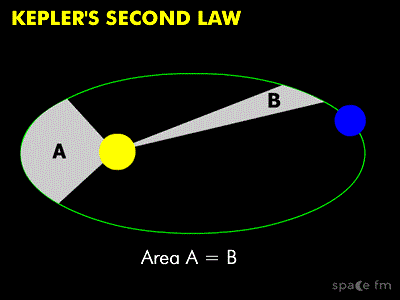
- Tercera Ley: Para cualquier planeta, el cuadrado de su período orbital es directamente proporcional al cubo de la longitud del semieje mayor de su órbita elíptica.
Demostración matemática de dichas leyes
Primera Ley: Cónica y en concreto una elipse
Todos los planetas se desplazan alrededor del Sol describiendo órbitas elípticas. El Sol se encuentra en uno de los focos de la elipse.
Primera Ley de Kepler
Para poder demostrar esta primera ley (La órbita de los planetas es elíptica), partiremos de la Ley de Gravitación Universal:
\(\displaystyle \vec{F} = -\frac{G\cdot M\cdot m}{r^{2}} \cdot \frac{\vec{r}}{r}\)
Donde \(\displaystyle \vec{r}\) es el radiovector que une el Sol con el planeta (En ese sentido y con origen en el Sol, \(\displaystyle M\) es la masa del Sol y \(\displaystyle m\) la masa del planeta.
El valor de la aceleración que experimenta el planeta es:
\(\displaystyle \vec{a} = \frac{\vec{F}}{m} = \ddot{\vec{r}} = -\frac{G\cdot M}{r^{2}} \cdot \frac{\vec{r}}{r}\)
Realmente todos sabemos que la Ley de Gravitación Universal expresa la fuerza que ejerce un cuerpo sobre otro, y que se presenta a pares, es decir, que la misma fuerza que el Sol ejerce sobre el planeta, es ejercida por el planeta sobre el Sol.
Sin embargo, la aceleración que experimenta un cuerpo es proporcional a la fuerza e inversamente proporcional a su masa, es decir, que un cuerpo tan masivo como el Sol sufre una aceleración casi despreciable en comparación con el planeta. De hecho, siendo rigurosos, un planeta no sólo sufre la fuerza del Sol, sino que se ve afectado por el resto de cuerpos del Sistema Solar (Por ejemplo a la Tierra le afecta la Luna y uno de sus efectos más apreciables son las mareas). Además, los cuerpos celestes no son esferas perfectas de densidad homogénea, por lo que no deberíamos de poder aplicar dicha ecuación tan a la ligera.
Todas estas consideraciones se reúnen bajo el concepto de perturbaciones. Sin embargo, a grandes rasgos y sin alejarnos demasiado de la realidad, se suele estudiar con generalidad el problema kepleriano de los 2 cuerpos, donde estos se aíslan del resto del universo.
Además, en el caso del Sol y un planeta como la Tierra, la masa del Sol es tan grande que el centro de gravedad de dicho sistema de masas se encuentra prácticamente en el Sol, por lo que podemos obtener un resultado muy cercano a la realidad si suponemos que el Sol «no se mueve».
Una vez dicho todo esto, la Ley de Gravitación Universal nos proporciona una ecuación diferencial que, tras resolverla, nos aportaría la ecuación del movimiento del planeta.
Para reducir el número de constantes, se define el parámetro gravitacional como \( \mu = G \cdot M \)
A continuación haré un desarrollo por pasos para la obtención de la solución (Es bastante avanzado, puede ignorarse).
Multiplicando vectorialmente a ambos lados de la ecuación por el momento cinético específico \(\displaystyle \vec{h}=\vec{r} \times \vec{v}\) llegamos a:
\(\displaystyle \ddot{\vec{r}} \times \vec{h} = – \mu \frac{\vec{r} \times \vec{h}}{r^{3}}\)
\(\begin{aligned} (1) & \quad \frac{d}{dt}(\dot{\vec{r}} \times \vec{h}) = \ddot{\vec{r}} \times \vec{h} + \dot{\vec{r}} \times \dot{\vec{h}} = \ddot{\vec{r}} \times \vec{h} \\ (2) & \quad -\mu \frac{\vec{r} \times (\vec{r} \times \vec{v})}{r^{3}} = -\mu \frac{(\vec{r} \cdot \vec{v}) \cdot \vec{r} – (\vec{r} \cdot \vec{r}) \cdot \vec{v}}{r^{3}} = -\mu \frac{\dot{r} \cdot \vec{r} – r \cdot \vec{v}}{r^{2}} = \frac{d}{dt} \left(\frac{\mu \cdot \vec{r}}{r}\right) \end{aligned}\)
Eliminando \(\dot{\vec{h}}\) al ser el momento específico siempre constante como se demostrará más tarde. Por lo tanto:
\(\displaystyle \frac{d}{dt}\left (\dot{\vec{r}} \times \vec{h} – \frac{\mu \cdot \vec{r}}{r}\right ) = 0\)
\( \displaystyle \vec{v} \times \vec{h} – \frac{\mu \cdot \vec{r}}{r} = \vec{cte} = \mu \cdot \vec{e}\)
Donde \(\displaystyle \vec{e}\) es el vector de Laplace o vector excentricidad, y lo definimos de forma que apunta al periapsis (Según nuestro sistema de referencia, hacia el eje positivo x)
Tomando producto escalar de la última ecuación con \(\displaystyle \vec{r}\) y siendo \(\displaystyle \theta\) definida como la anomalía verdadera (Ángulo que forma el radiovector \(\displaystyle \vec{r}\) con el eje x:
\(\displaystyle \vec{r} \cdot \vec{v} \times \vec{h} – \frac{\mu \cdot \vec{r} \cdot \vec{r}}{r} = \mu \vec{e} \cdot \vec{r}\)
Recordando que \(\displaystyle \begin{matrix}\vec{r} \cdot \vec{v} \times \vec{h} = \vec{h} \cdot \vec{r} \times \vec{v} = h^{2} \ \ & y & \ \ \vec{r} \cdot \vec{e} = r \cdot e \cdot cos(\theta) \end{matrix} \rightarrow\)
\(\boxed{\displaystyle \rightarrow h^{2} – \mu \cdot r = \mu \cdot r \cdot e \cdot cos(\theta)}\)
\(\boxed{\displaystyle r(\theta) = \frac{\frac{h^{2}}{\mu}}{1+ e \cdot cos(\theta)} = \frac{p}{1+ e \cdot cos(\theta)}} \)
Es decir, la ecuación de una cónica (Elipse, parábola o hipérbola), donde:
- \(\displaystyle p \) es el parámetro gravitacional. En el caso de la elipse, sus parámetros son:
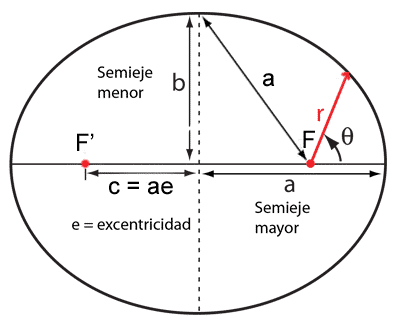
- \( \displaystyle e \) es la excentricidad, que representa:
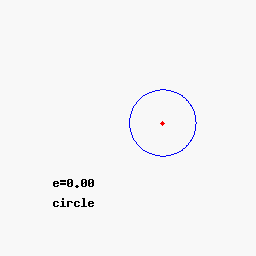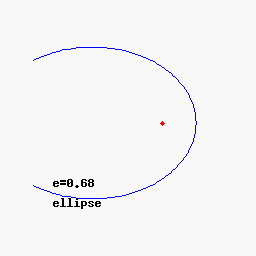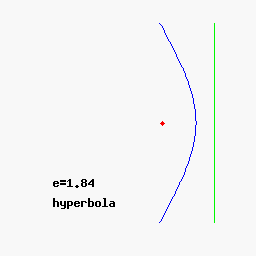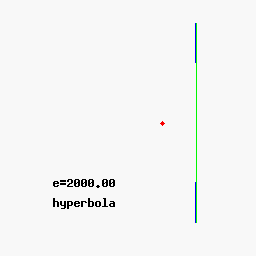
- Si e=0 -> Ecuación de una circunferencia (Caso particular de la elipse).
- Si 0<e<1 -> Ecuación de elipse.
- Si e=1 -> Ecuación de parábola (Órbita abierta).
- Si e>1 -> Ecuación de hipérbola (Órbita abierta).
Podéis variar los parámetros para comprobar las distintas trayectorias aquí
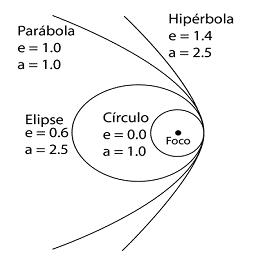
De las observaciones de Kepler se extraen 2 conclusiones:
- Los planetas siguen órbitas cerradas, es decir, no «escapan» del Sistema Solar.
- La velocidad de los planetas no es constante.
Por lo tanto, el único tipo de órbita que puede seguir un planeta es la elíptica.
(Otros cuerpos presentes en el Sistema Solar como cometas, meteroides, asteroides… orbitan entorno al Sol con órbitas elípticas o hiperbólicas. Los casos circular y parabólico son casos ideales donde la excentricidad toma un valor exacto, lo cual no se da de forma natural en la realidad ya que la mínima perturbación cambiaría el tipo de órbita. Sin embargo, planetas como la Tierra lo hacen con una excentricidad cercana a 0 (e ≈ 0.0167), por lo que la suposición de movimiento circular alrededor del Sol no distaría tanto de la realidad).
Momento cinético específico
En este subapartado voy a demostrar que el momento cinético específico (Momento cinético dividido entre la masa del planeta) es constante. Y de dicha solución obtendremos la conclusión de que las órbitas además de ser elípticas son planas.
Recordando la ecuación diferencial del movimiento:
\(\displaystyle \ddot{\vec{r}} = -\frac{G\cdot M}{r^{2}} \frac{\vec{r}}{r}\)
Multiplicando vectorialmente por \(\displaystyle \vec{r}\):
\(\displaystyle \vec{r} \times \ddot{\vec{r}} = -\frac{G \cdot M}{r^{2}} \cdot \frac{\vec{r} \times \vec{r}}{r}=0\)
Obtenemos una forma equivalente en forma de derivada temporal:
\(\displaystyle \frac{d}{dt} (\vec{r} \times \dot{\vec{r}}) = \dot{\vec{r}} \times \dot{\vec{r}} + \vec{r} \times \ddot{\vec{r}}=\vec{r} \times \ddot{\vec{r}}\)
Por lo tanto, combinando ambas ecuaciones:
\(\displaystyle \frac{d}{dt} (\vec{r} \times \dot{\vec{r}}) =0 \iff \vec{r} \times \dot{\vec{r}} = \vec{r} \times \vec{v} = \vec{h} = \vec{cte}\)
Como \(\displaystyle \vec{r} \cdot \vec{h} = 0\) , \(\displaystyle \vec{v} \cdot \vec{h} = 0\) y \(\vec{h}\) es constante, el movimiento se da en un plano perpendicular a \(\displaystyle \vec{h}\).
Segunda Ley: Momento cinético constante
El radiovector que une un planeta y el Sol barre áreas iguales en tiempos iguales.
Segunda Ley de Kepler
La demostración de esta segunda ley puede hacerse en el caso sencillo (Circular) o en el caso realista (Elíptico). Lo que tienen en común ambos casos es que se basan en la conservación del momento cinético.
Primero demostraré el caso cónico para posteriormente y con las consideraciones del caso circular exponer una demostración más sencilla.
Caso cónico
En primer lugar establecemos un sistema de referencia local en el plano orbital con origen en cada punto de la trayectoria \(\displaystyle \vec{r}(t)\) de forma que el vector \(\displaystyle \vec{e_{r}}\) es paralelo a \(\displaystyle \vec{r}\) y el vector \(\displaystyle \vec{e_{\theta}}\) está rotado 90º en sentido antihorario respecto a este de forma que:
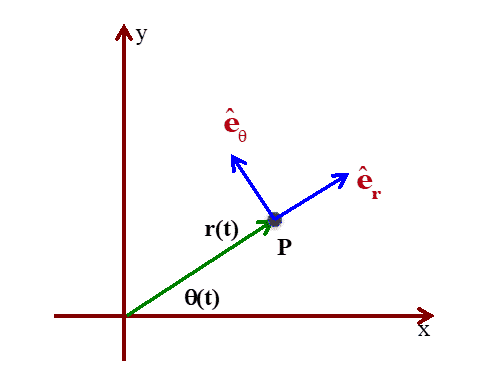
Por lo tanto:
\(\displaystyle \vec{r}=r \cdot \vec{e_{r}}\) \(\displaystyle \vec{v}=\frac{d \vec{r}}{dt} = \dot{r} \cdot \vec{e_{r}} + r \cdot \dot{\theta} \cdot \vec{e_{\theta}}\)Y entonces:
\(\displaystyle \boxed{\vec{h} = \vec{r} \times \vec{v} = r^{2} \cdot \dot{\theta} \cdot \vec{e_{z}}}\)
Una vez obtenida la expresión del momento cinético específico en nuestro sistema de referencia, nos centramos en el área. Un fragmento de área en coordenadas polares es:
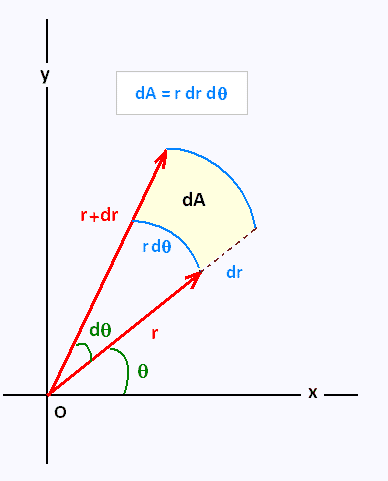
Por lo tanto, el área total barrida por el radiovector en un cierto tiempo partiendo desde el eje x se obtiene mediante la siguiente expresión:
\(\displaystyle A(t) = \int_{0}^{\theta (t)} \int_{0}^{r(\psi)} \rho \, d\rho \, d\psi = \int_{0}^{\theta (t)} \frac{r(\psi)^{2}}{2} \, d\psi\)
Si queremos calcular el área barrida por unidad de tiempo, derivamos y aplicamos el Teorema de la Cadena + Teorema Fundamental del Cálculo:
\(\boxed{{\displaystyle {\dfrac {\mathop {} \!\mathrm {d} }{\mathop {} \!\mathrm {d} x}}{\int _{a(x)}^{b(x)}f(t)\mathop {} \!\mathrm {d} t}=f(b(x))\cdot b^{\prime }(x)-f(a(x))\cdot a^{\prime }(x)}}\)
\(\displaystyle \frac{d}{dt}A(t) = \dot{A}(t) =\frac{d}{dt} \int_{0}^{\theta (t)} \frac{r(\psi)^{2}}{2} \ d\psi = \frac{r^{2} \dot{\theta}}{2} = \frac{h}{2} = cte\)
Y así obtenemos el resultado de que se barren áreas iguales en tiempos iguales (Se barre el mismo área por unidad de tiempo todo el rato), es decir, que la velocidad areolar es constante. Al ser \(\displaystyle h = r(t)^{2} \cdot \dot{\theta}(t) = cte\) , a mayor distancia (Mayor r), menor es la velocidad a la que se recorre la órbita y viceversa.
Caso circular
Una forma sencilla de demostrar la 2ª Ley de Kepler sin meternos en integrales es en el caso de asumir un movimiento circular.
En el caso de órbita circular, la velocidad es constante y forma siempre 90º con el radiovector. Su valor es:
\(\displaystyle v = r \cdot w = r \cdot \dot{\theta} = cte \)
Y por lo tanto, el valor de \(\displaystyle h\) es inmediato: \(\displaystyle h = r \cdot v = r^{2} \cdot \dot{\theta}\)
Como obviamente el radio es constante, sabemos que la expresión del área que se recorre es:
\( \displaystyle dA = \frac{r^{2}}{2} d\theta\) y, por lo tanto, \( \displaystyle \frac{dA}{dt} = \frac{r^{2} \dot{\theta}}{2} = \frac{h}{2} = cte\)
Tercera Ley: Relación entre área total y velocidad areolar
Una vez demostradas las 2 primeras leyes, la demostración de la 3ª se vuelve muy sencilla.
Para cualquier planeta, el cuadrado de su período orbital es directamente proporcional al cubo de la longitud del semieje mayor de su órbita elíptica.
Tercera Ley de Kepler
Sabemos que el valor del área de una elipse es \(A=\pi a b\), coincidiendo con el área de una circunferencia en el caso particular de \( \displaystyle a=b=r \).
Puesto que conocemos \(\displaystyle \dot{A}\) de la demostración anterior, el período de una órbita viene dado por:
\( \displaystyle T = \frac{A}{\dot{A}} = \frac{\pi a b}{\frac{h}{2}}=\frac{2 \pi a b}{h}\)
Expresando \(\displaystyle b\) y \( \displaystyle h \) en función de \( \displaystyle a \) y \( \displaystyle e \):
\( \displaystyle b = a\sqrt{(1-e^{2})}\) \( \displaystyle h = \sqrt{p \cdot \mu} = \sqrt{a\cdot (1-e^{2})\cdot \mu}\)Introduciendo los términos en la expresión del periodo:
\( \displaystyle T =\frac{2 \pi a^{2}\sqrt{(1-e^{2})} }{\sqrt{a\cdot (1-e^{2})\cdot \mu}} = \frac{2 \pi \sqrt{a^{3}}}{\sqrt{\mu}} \)
Elevando ambos términos al cuadrado:
\(\displaystyle \boxed{T^{2} = \frac{4 \pi ^{2}}{\mu} \cdot a^{3}}\)
Quedando demostrada la 3ª Ley de Kepler y obteniendo la constante que relaciona dichos parámetros.
Las matemáticas son muy útiles y es una herramienta que hemos inventado para que nos ayude a materializar conceptos abstractos; es nuestra amiga, no nuestra enemiga.
Si te gusta comprender las cosas empleando el lenguaje matemático, te recomiendo este artículo que hice donde empleando álgebra muy básico comprenderás cómo pasar a fracción cualquier número decimal ¡Sin memorizar absolutamente ninguna fórmula!