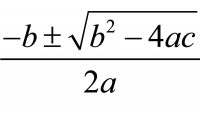Todo el mundo sabe lo que es una raíz cuadrada, o al menos le suena. Se identifica con el símbolo “√”, y al hacer la raíz cuadrada de un número \(n\) lo que buscamos es un número \(m\) tal que su cuadrado sea el primer número, es decir:
\(\sqrt{n} = m \iff m^{2} = n\)
Es relativamente sencillo y directo calcular la raíz cuadrada de un número cuadrado o cuadrado perfecto, es decir, un número cuya raíz cuadrada es un número natural. Ejemplos de estas raíces serían \(\sqrt{4} = 2\), \(\sqrt{25} = 5\), \(\sqrt{64} = 8\)…
Sin embargo, la cosa se complica cuando tenemos que calcular la raíz cuadrada de un número cuyo valor no es un número natural, como puede ser por ejemplo \(\sqrt{50} = ?\).
En este artículo vamos a aprender razonadamente a cómo estimar la raíz cuadrada de cualquier número a mano. Empleando el Cálculo llegaremos a una fórmula que nos permitirá aproximar el valor de cualquier raíz cuadrada sin usar la calculadora.
Aproximación de una raíz cuadrada usando el Cálculo
Hay muchos métodos para calcular raíces cuadradas como pueden ser el método de factorización, método de estimación por aproximación sucesiva, método babilónico… Pero yo voy a desarrollar un método basado en el Cálculo, es decir, el uso de funciones y derivadas.
Digamos que queremos calcular la raíz cuadrada de un número \(x\). La solución de dicha raíz puede expresarse de manera funcional tal que \(f(x) = \sqrt{x}\). De esta forma, \(f(4) = 2, f(25) = 5\), etc…
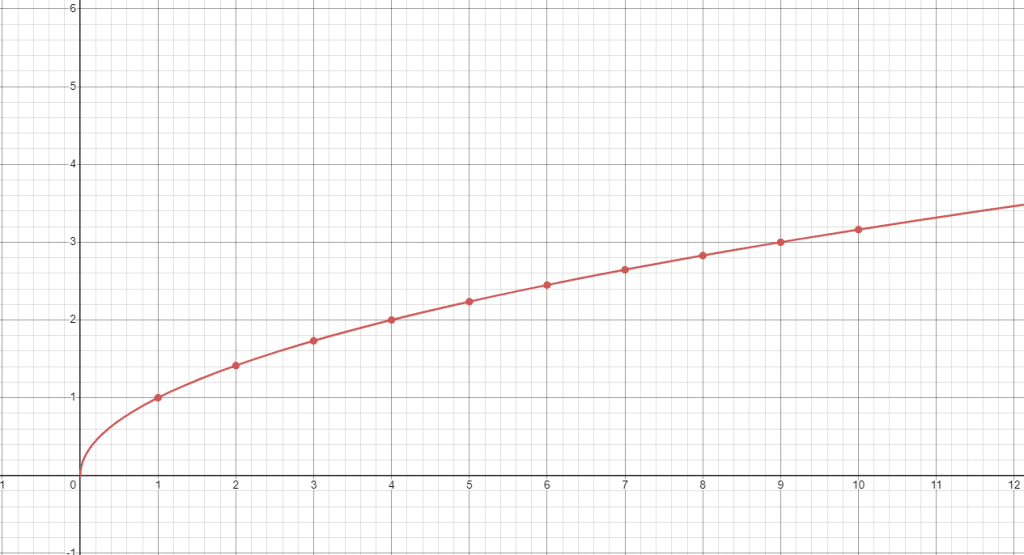
Digamos que queremos calcular la raíz cuadrada de 50, es decir, \(f(50) = \sqrt{50}\)
Dicho número no es un número cuadrado. No obstante, cercano a ese valor tenemos el 49, del cual sabemos que \(f(49) = \sqrt{49} = 7\).
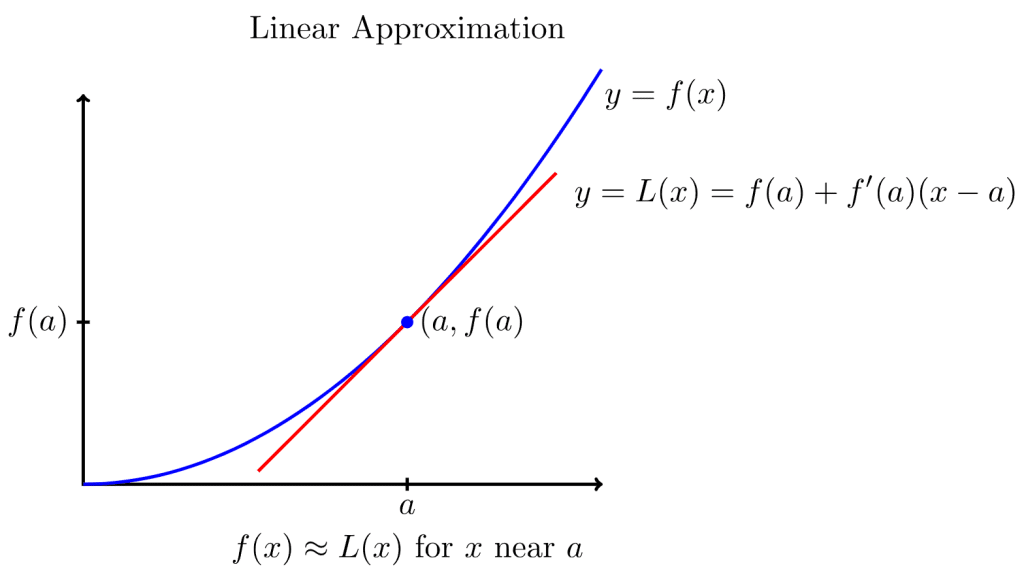
Podemos aproximar el valor de una función a partir de un punto de su entorno si la linealizamos, es decir, obtenemos la tangente de la curva de la función en dicho punto (básicamente calculamos su derivada) y la recorremos hasta el valor que buscamos. Es decir, si queremos linealizar una función en torno a un punto \(a\), la aproximación sería:
\(f(x) \approx f(a) + f'(a)(x-a)\)
Como nuestra función original era \(f(x) = \sqrt{x}\), su derivada es \(f'(x) = \dfrac{1}{2 \sqrt{x}}\), y la fórmula general quedaría:
\( f(x) = \sqrt{x} \approx \sqrt{a} + \dfrac{1}{2 \sqrt{a}}(x-a)\)
Sustituyendo los valores con \(a=49\) y particularizando para \(x=50\), nos queda:
\(f(50) \approx f(49) + f'(49)(50-49)\)
\(f(50) \approx 7 + \dfrac{1}{14}\)
Tendríamos por lo tanto que calcular \(\dfrac{1}{14}\) a mano, que no es directo pero no es una tarea difícil. Nos queda un número irracional que truncamos al tercer decimal: \(\dfrac{1}{14} \approx 0.071\)
Por lo tanto, nuestra aproximación nos quedaría:
\(f(50) \approx 7.071\)
SI calculamos el error relativo con respecto a la raíz cuadrada de 50, nos queda:
\(\dfrac{|7.071-\sqrt{50}|}{\sqrt{50}} \cdot 100 = 0.001\%\)
Es decir, que prácticamente hemos clavado el valor de la raíz cuadrada, demostrando la eficacia de este método.
Vamos a hacer lo mismo con otro número, digamos \(\sqrt{152}\)
Los números cuadrados más cercanos son:
\(\sqrt{144} = 12\)
\(\sqrt{169} = 13\)
Partimos por lo tanto del 144. Sustituyendo en la fórmula de aproximación:
\(f(152) \approx f(144) + \dfrac{1}{2 \sqrt{144}} (152-144)\)
\(f(152) \approx 12 + \dfrac{1}{24} (8) \approx 12 + \dfrac{1}{3} \approx 12,33\)
SI calculamos el error relativo con respecto a la raíz cuadrada de 152, nos queda:
\(\dfrac{|12,33-\sqrt{152}|}{\sqrt{152}} \cdot 100 = 0.01\%\)
De nuevo un error extremadamente bajo. Obviamente cuanto mayor es la diferencia entre el punto de partida y el valor que queremos calcular, mayor va a ser el error. Por otra parte, cuanto mayor es el valor de la raíz a calcular, menor error existe al linealizar al tender la derivada a 0 en el infinito: \(f'(x \rightarrow \infty) = 0\)
Otros métodos
Si buscamos en internet otros métodos para estimar la raíz cuadrada de un número cualquiera, muchas veces nos aparece la siguiente fórmula:
\(\sqrt{x} \approx \dfrac{x+a}{2\sqrt{a}}\)
Esta no es ninguna fórmula mágica que aparece porque si. SI volvemos a nuestra aproximación y agrupamos términos:
\(\sqrt{x} \approx \sqrt{a} + \dfrac{1}{2 \sqrt{a}}(x-a)\)
\(\sqrt{x} \approx \dfrac{2a}{2 \sqrt{a}} + \dfrac{1}{2 \sqrt{a}}(x-a)\)
\(\sqrt{x} \approx \dfrac{2a + x – a}{2 \sqrt{a}} \)
\(\sqrt{x} \approx \dfrac{x+a}{2\sqrt{a}}\)
Al final en las matemáticas no existen fórmulas mágicas que aparecen porque si. Otro claro ejemplo de esto es de dónde sale La famosa fórmula de ecuaciones de segundo grado. Todo está relacionado y todo parte de un mismo punto y nos lleva al mismo destino siempre que apliquemos rigurosamente las normas. Es exactamente lo que quise transmitir en el artículo Las matemáticas es el lenguaje con el que Dios ha escrito el universo y que recomiendo encarecidamente leer si esto te llama la atención.