Introducción
¡Buenas! En esta primera entrada acerca de las cónicas vamos a hablar de la más sencilla, la más conocida y la más estudiada: la circunferencia.
Se denomina cónica o sección cónica a la curva resultante de la intersección entre un cono y un plano. Existen cuatro cónicas: circunferencias, elipses, parábolas e hipérbolas.
La circunferencia se genera cuando cortamos un cono con un plano perpendicular al eje de dicho cono. Se podría decir que es un caso particular de elipse en el que el plano tiene mínima inclinación.
Ecuación de la circunferencia
La circunferencia se define como los puntos del plano que equidistan la misma distancia de un punto fijo llamado centro. (Lo llamaremos C)
Tomamos un punto genérico contenido en la circunferencia denominado P(x,y), y situamos el centro de la circunferencia en un punto fijo C(a,b) tal que a y b son las coordenadas del centro en los ejes x-y. Nuestro radio es r
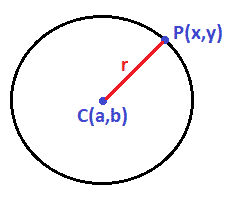
La definición de la circunferencia nos dice que \(d(P(x,y),C(a,b))=r\), siendo r el radio constante.
Se sabe que la distancia entre 2 puntos en el plano x-y es: \(d(P_{1},P_{2})=\sqrt{(x_{2}-x_{1})^{2}+( y_{2}-y_{1} )^{2}}\)
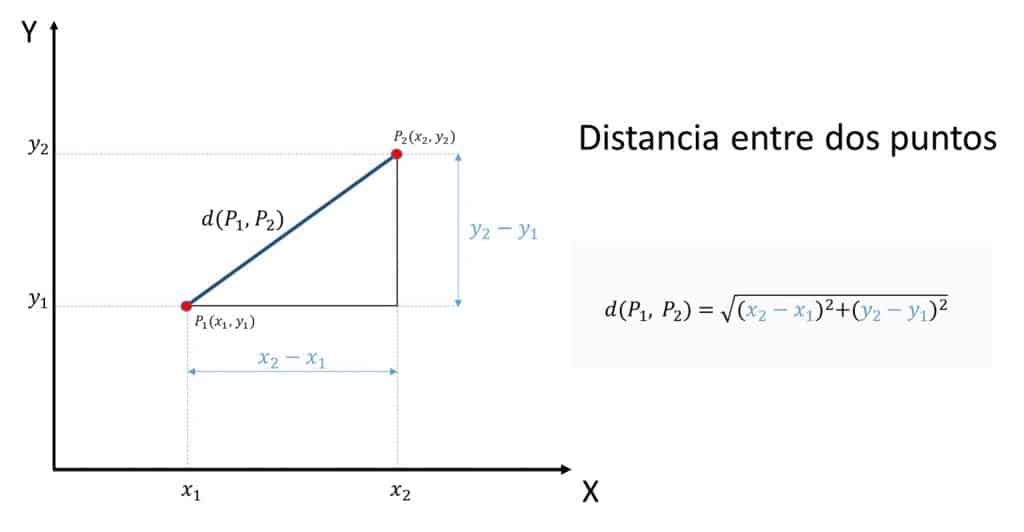
Siendo nuestros puntos P(x,y) y C(a,b), con coordenadas (x,y) y (a,b) respectivamente, la distancia nos queda:
\( d(C(a,b),P(x,y))= \sqrt{(x-a)^{2}+( y-b)^{2}}=r\)Y, finalmente, quitando las raíces llegamos a:
\( (x-a)^{2}+( y-b)^{2} =r^{2}\)Siendo (a,b) las coordenadas del centro de la circunferencia. Para una circunferencia centrada en el origen de coordenadas la ecuación queda \( x^{2}+ y^{2} =r^{2}\)
Parametrización
En la ecuación anterior tenemos una restricción y 2 variables. Es decir, una curva. Es problemático querer pintar dicha curva empleando directamente las variables x e y ya que, si queremos ir variando x por ejemplo, debemos de calcular el valor de y que debe de coincidir en todo momento con el valor esperado. Y como podréis comprobar, hay raíces de por medio, de forma que si no operamos con el cuidado necesario acabaremos pintando sólo media circunferencia (Que es lo que ocurre si intentamos generar una gráfica y=f(x) para representar la circunferencia).
Para solucionar este problema recurrimos a una parametrización. De esta forma, las variables x e y se relacionan de forma que variando una tercera variable obtenemos el valor esperado de x e y automáticamente. Para ello empleamos las coordenadas polares.
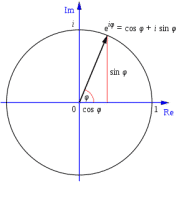
Recordamos la fórmula fundamental de la trigonometría: \(cos ^{2} (\theta) +sen ^{2} (\theta)= 1\)
¿Os suena de algo? ¿Podríamos adaptarla a nuestra fórmula? Vamos a probar.
Si hacemos: \(\left\{ \begin{matrix} x = \cos(\theta) \\ y = \sin(\theta) \end{matrix} \right.\) Casi obtenemos lo que buscamos. Nos falta añadir el radio r y el caso en el que el centro no se encuentre en el (0,0)
Para ello recurriremos a la siguiente parametrización:
\(\left\{ \begin{matrix} x = r \cdot \cos(\theta) + a \\ y = r \cdot \sin(\theta) + b \end{matrix} \right.\)De forma que se cumple la relación:
\((x-a)^{2}+( y-b)^{2} =r^{2}\rightarrow\) \(\rightarrow( r*cos(\theta)+a -a)^{2}+ (r*sen(\theta)+b -b)^{2}=r^{2}*( cos ^{2} (\theta)+ sen ^{2} (\theta) )=r^{2} \)De esta forma pintamos la circunferencia en sentido antihorario comenzando por el eje x. Podríamos intercambiar el seno y el coseno y/o añadir desfase para cambiar la forma en la que «pintamos» la circunferencia.
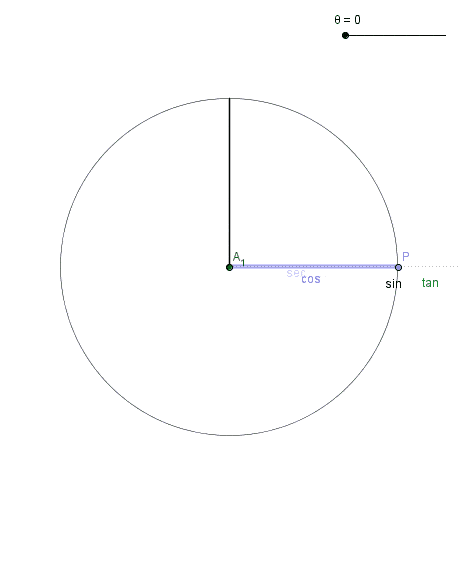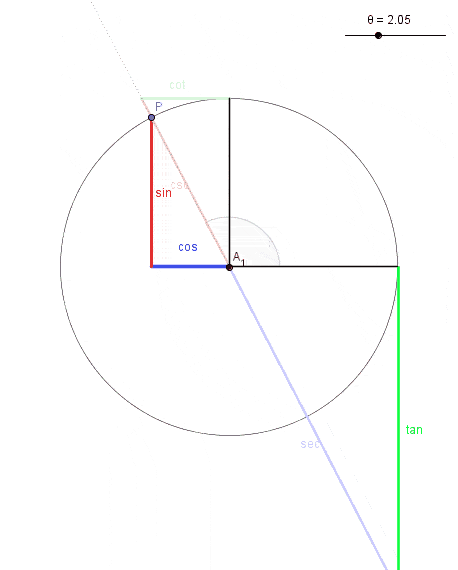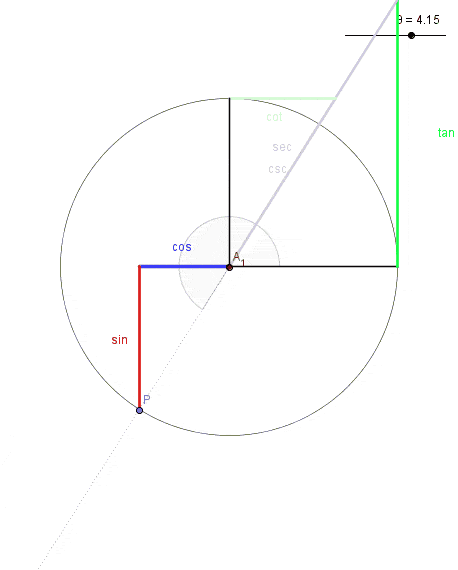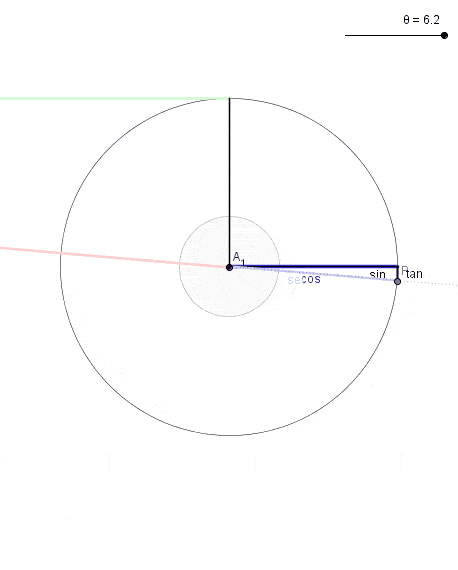
Si quisiésemos pintar el círculo, es decir, la circunferencia y todo su interior, deberíamos de variar en esa parametrización \(\theta\) entre \(0 \ y \ 2\pi\) y nuestra \(r\) entre \(0 \ y \ R\). De esta forma, si integramos podemos hallar el área de dicho círculo integrando las 2 variables así como la longitud de la circunferencia integrando 1 variable. Para más información:



Exelentes soluciones y demostraciones de geometría analítica me gustan y puedo contar con su ayuda
Marcial Alcántara