
¡Buenas! En esta entrada escribiré acerca del teorema de la bola peluda. No nos dejemos engañar por el nombre, puesto que a pesar de parecer gracioso, tiene unas implicaciones brutales en la topología diferencial.
¿Por qué se llama así?
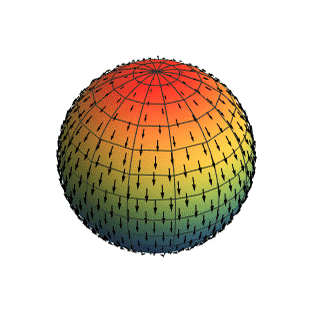
Para entender el teorema, primero haremos una analogía con algo cotidiano; una bola peluda:
Imaginemos que cogemos un peine y queremos peinarla, tal que todos los pelos se orienten en una dirección. En el caso de intentar peinar en una dirección lateralmente se produciría un «remolino» en la parte superior e inferior de la esfera (2 puntos discontinuos). En caso de peinar desde arriba hacia abajo se crearían 2 puntos con discontinuidad en ambas partes superior e inferior (2 puntos discontinuos).
El teorema
Antes de nada, la traducción de «Pelos peinados» en lenguaje matemático es «Campo de vectores tangente», y se define tal que:
Un campo de vectores tangente sobre una superficie de \( R^{3} \) es una aplicación que asocia a cada punto de la superficie un vector tangente a la misma en dicho punto. Considerando \( S^{2} \) a la superficie generada por la esfera, dicho campo de vectores es una aplicación \( V:S^{2}->R^{3} \) tal que para cada punto \( P \) de \( S^{2} \) se tiene que \( V(P) \) genera un vector que parte de dicho punto y es tangente a la superficie.
El teorema dice asi:
Dada una superficie \(S^{2}\) continua que pueda deformarse hasta convertirse en una esfera, y un campo vectorial \(\ \ V(P)\) tangente a dicha superficie en todo punto \(P\) , existe al menos un punto \(P_{0}\) tal que \(V(P_{0})=0\)
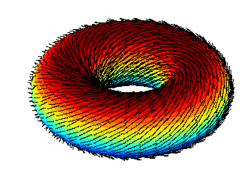
Con lo cual, queda excluido el caso de toroides, en los que con relativa facilidad se demuestra que no es necesaria la existencia de dicha discontinuidad:
Implicaciones
La primera implicación es clara: No vas a poder peinarte sin que aparezca un remolino. Bueno, miento. En el caso de que tuvieras toda la cabeza cubierta de pelo ocurriría a ciencia cierta. No obstante, el teorema garantiza que existe como mínimo 1 punto. Es por ello que, a pesar de no tener la cabeza llena de pelos, todo el mundo tiene como mínimo 1 remolino, y hay personas que incluso tienen 2 o 3.
Otra implicación importante a gran escala es el tema del viento. El viento como tal es un campo vectorial tangente a la superficie de la tierra… ¿Y qué significa eso? Que en todo momento existe un punto en el planeta en el que se está produciendo un ciclón o anticiclón. Y el «ojo del huracán» es, ni más ni menos, que dicho punto.

Parametrización de esfera
Otra implicación es la presencia inevitable de uno o más puntos con plano tangente discontinuo en la parametrización de una esfera.
Con una parametrización de la superficie de la esfera de radio unidad:
\(\left\{ \begin{matrix} x = \sin(\theta)\cdot\cos(\phi) \\ y = \sin(\theta)\cdot\sin(\phi) \\ z = \cos(\theta) \end{matrix} \right. \quad \text{with} \quad \left\{ \begin{matrix} 0 \leq \phi \leq 2\pi \\ 0 \leq \theta \leq \pi \end{matrix} \right.\)Y de acuerdo a la siguiente notación:
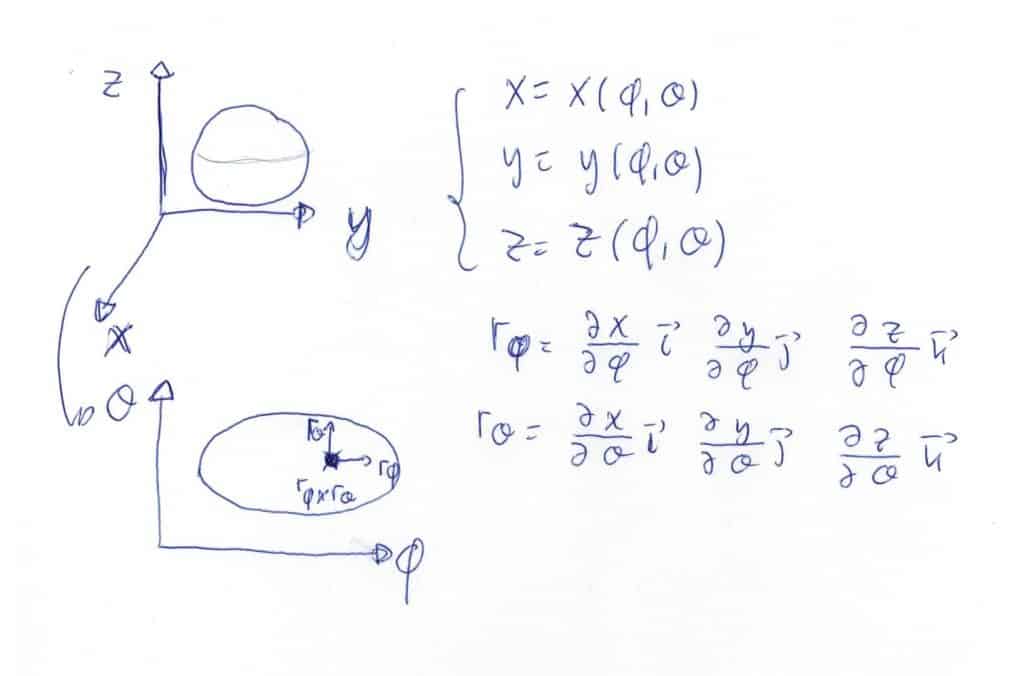
Siendo \(r_{\phi} \times r_{\theta}\) el vector perpendicular a la superficie (Vector director del plano tangente) y desarrollando los cálculos, se llega a que \(r_{\phi} \times r_{\theta}=sen(\theta)*(sen(\theta)cos(\phi),-sen(\theta)sen(\phi),cos(\theta))\)
Quedando patente la discontinuidad de dicho plano tangente en los puntos con \(\theta=0 \ y \ \pi\), es decir, en los polos.




Jaja que curioso!