En este artículo voy a presentar el desarrollo y solución de un problema de Aeroelasticidad (específicamente el fenómeno de Flameo) correspondiente a un examen parcial de la asignatura homónima del Máster de Ingeniería Aeronáutica de la Universidad de Sevilla. A continuación se presenta el enunciado:

Datos adicionales
Para las características de la placa se emplea un aluminio 6061-T6 cuyas propiedades son las siguientes:
\(\rho = 2700 \ kg/m^3\) \(E = 68.9 \ GPa\) \(G = 26 \ GPa\)El momento de inercia de área y el módulo de torsión se calcula, respectivamente, como:
\(I = \dfrac{1}{12} 2bt^{3}\) \(J = \dfrac{1}{3} 2bt^{3}\)La masa e inercia con respecto al eje y por unidad de envergadura se calcula, respectivamente, como:
\(m = 2 b t \rho\) \(i_{yG} = \dfrac{1}{12} m (2 b)^{2}\)Finalmente se toma la densidad del aire en condiciones normales:
\(\rho_{\infty} = 1.225 kg/m^{3}\)Planteamiento del problema
Para resolver el problema emplearemos el modelo de barra continua como aproximación. De esta manera, analizando una rebanada, podremos calcular los esfuerzos en la sección.
Una barra tiene infinitos grados de libertad. Sin embargo, cada sección presenta 6 grados de libertad (3 traslaciones y 3 rotaciones). No obstante, debido a las condiciones de contorno del problema y las fuerzas externas, sólo son no nulos los desplazamientos verticales en el eje z y los giros alrededor del eje x. Los esfuerzos los concentramos en el eje elástico, que es el punto en el que se aplica la Torsión, Flexión y Axil.
Como la placa tiene densidad constante la posición del centro de gravedad debe encontrarse a una distancia \(x_{G} = b\) del borde de ataque, y debido a las condiciones de contorno podemos decir que el eje elástico tambièn se encuentra en \(x_{e} = b\).
Definimos el desplazamiento vertical del eje elástico positivo con el eje z como una función que depende de la sección y el tiempo \(w(y,t) = w_{G}(y,t)\) y el giro alrededor de dicho eje positivo con el eje y de igual forma \(\alpha(y,t)\) donde dicho giro coincide con el ángulo de ataque de la placa.
A continuación se muestran los esfuerzos aplicados en la rebanada, considerando la sustentación aplicada en el centro de gravedad junto con un momento aerodinámico en dicho punto, las inercias en desplazamiento vertical y rotación alrededor del eje y, y el peso:
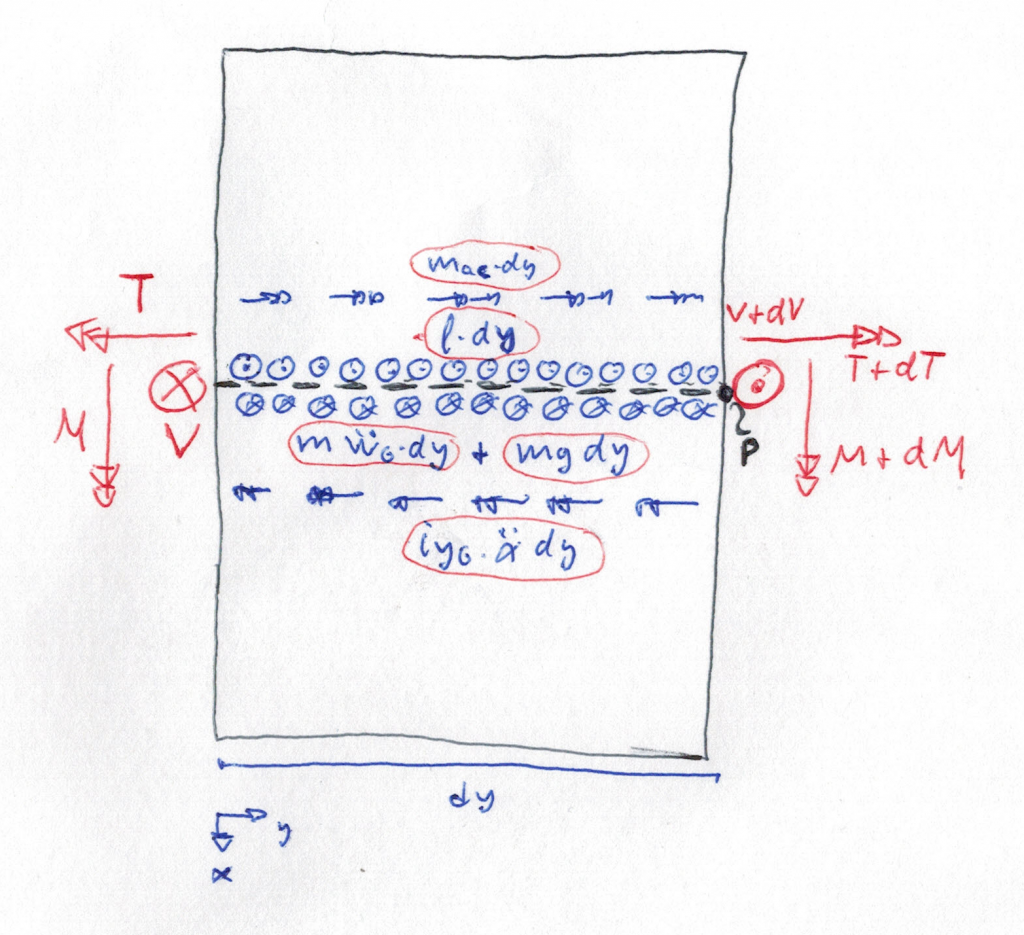
El sumatorio de fuerzas y momentos nos proporcionan las siguientes ecuaciones:
\(\displaystyle \sum F_{z} = 0 \rightarrow V + dV – V + l \cdot dy – mg \cdot dy – m \ddot w_{G} \cdot dy = 0\)
\(\displaystyle \sum M_{x}^{P} = 0 \rightarrow M + dM – M + V \cdot dy + (\dots) \cdot \underbrace{\dfrac{dy^{2}}{2}}_{neglected} = 0\)
\(\displaystyle \sum M_{y}^{P} = 0 \rightarrow T + dT – T + m_{ac} \cdot dy – i_{yG} \ddot \alpha \cdot dy = 0\)
Obsérvese que en el sumatorio de momentos alrededor del eje x hemos despreciado los momentos generados por las cargas distribuidas al ser de un orden de magnitud muy inferior (diferencial al cuadrado) así como que no hemos considerado la inercia de cada sección alrededor de dicho eje puesto que se asume que la energía cinética asociada al desplazamiento vertical de la sección es mucho mayor que la asociada al giro.
De la segunda ecuación obtenemos:
\(\boxed {V = – \dfrac{dM}{dy}}\)
Introduciendo dicho resultado en la primera ecuación obtenemos:
\(\dfrac{dV}{dy} = \boxed{- \dfrac{d^{2}M}{dy^{2}} = mg + m \ddot w_{G} – l}\)
La última ecuación resulta:
\(\boxed{\dfrac{dT}{dy} = – m_{ac}+ i_{yG} \ddot \alpha}\)
El modelo de barras nos proporciona una relación entre los esfuerzos y las deformaciones. Despreciando la deformación por cortante e incluyendo los datos de la placa (módulos e inercia) tenemos la siguiente relación:
\( \dfrac{M}{EI} = \dfrac{d^{2} w}{dy^{2}} \\\)
\(\dfrac{T}{GJ} = \dfrac{d \alpha}{dy}\)
Sustituyendo los esfuerzos obtenemos las ecuaciones en derivadas parciales para los dos grados de libertad:
\(EI \dfrac{\partial^{4} w (y,t)}{\partial y^{4}} + mg + m \dfrac{\partial ^{2} w (y,t)}{\partial t^{2}} – l = 0 \\\)
\(GJ \dfrac{\partial ^{2} \alpha}{\partial y^{2}} + m_{ac} – i_{yG} \dfrac{\partial ^{2} \alpha}{\partial t^{2}} = 0 \)
Para resolver las ecuaciones se empleará el método de Galerkin. Definimos cada variable \(w(y,t), \alpha(y,t)\) como un sumatorio de funciones independientes tal que:
\(\displaystyle w(y,t) = \sum_{i=1}^{n} F_{i}(y) \cdot W_{i}(t)\) \(\displaystyle \alpha(y,t) = \sum_{i=1}^{m} H_{i}(y) \cdot A_{i}(t)\)Donde las funciones \(F_{i}(y),H_{i}(y)\) representan el modo de deformación que adquiere la barra en cada sección y \(W_{i}(t),A_{i}(t)\) la magnitud de cada uno de los modos de deformación en cada instante de tiempo.
Condiciones de contorno
En y=0
La placa en dicho extremo se encuentra apoyada en muelles en las esquinas. Sustituyendo los muelles por la reacción y visualizando los esfuerzos internos se tiene el siguiente esquema:
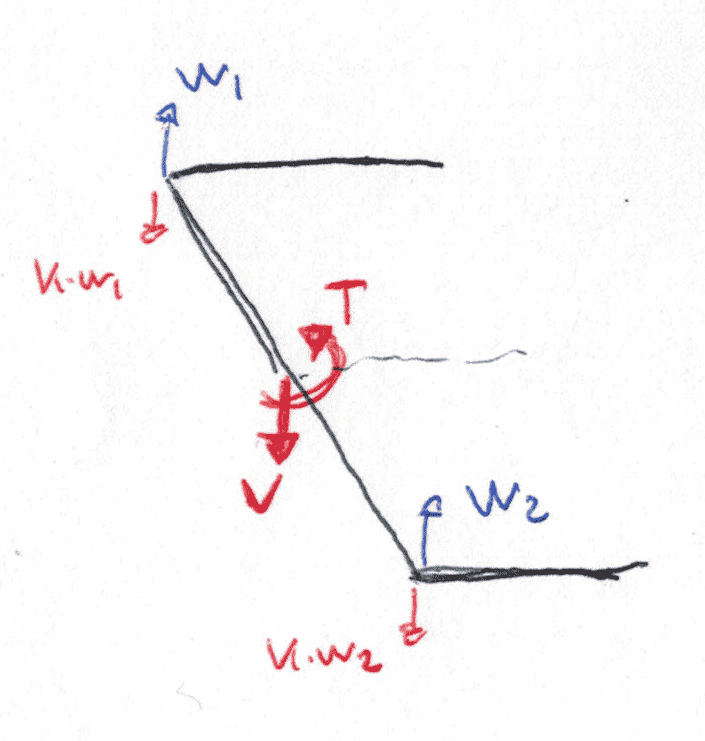
Los desplazamientos en las esquinas se componen de desplazamiento del eje elástico + giro de la sección:
\(w_{1} = w(0,t) + \alpha(0,t) \cdot b \\\) \(w_{1} = w(0,t)- \alpha(0,t) \cdot b\)1) Flector nulo
\(M(0,t) = 0 = EI \dfrac{d^{2} w(0,t)}{dy^{2}} \iff w»(0,t) = 0 \iff \boxed{ F_{i}»(0) = 0}\)2) Cortante equivalente
\(V(0,t) = k (w_{1} + w_{2}) = 2kw(0,t) = -EI w»'(0,t) \iff \boxed{F_{i}(0) = -\dfrac{EI}{2k} F_{i}»'(0)}\)3) Torsor equivalente
\(T(0,t) = k w_{1} b – k w_{2} b = 2 k b^{2} \alpha(0,t) = GJ \alpha'(0,t) \iff \boxed{H_{i}(0) = \dfrac{GJ}{2kb^{2}} H_{i}'(0)}\)En y=s
La placa en dicho extremo se encuentra apoyada en el eje elástico. Sustituyendo el apoyo por la reacción se tiene el siguiente esquema:
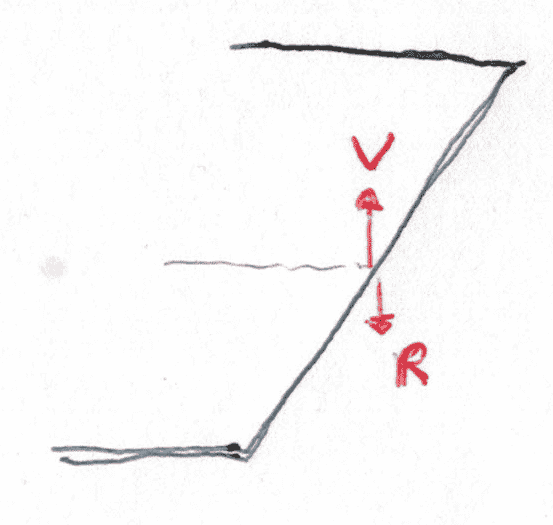
1) Desplazamiento nulo
\(w(s,t) = 0 \iff \boxed{F_{i}(s) = 0}\)2) Flector nulo
\(M(s,t) = 0 = EI \dfrac{d^{2} w(s,t)}{dy^{2}} \iff w»(s,t) = 0 \iff \boxed{ F_{i}»(s) = 0}\)3) Torsor nulo
\(T(s,t) = 0 = GJ \alpha'(s,t) \iff \boxed{H_{i}'(s) = 0}\)Funciones de aproximación
Como funciones de aproximación se emplearan funciones polinómicas tal que:
\( F_{i} = a_{0} + a_{1} \left (\dfrac{y}{s} \right ) +a_{2} \left(\dfrac{y}{s} \right)^{2} + a_{3} \left(\dfrac{y}{s} \right) ^{3} + \left(\dfrac{y}{s} \right)^{3+i} \)
Con \(i \in [1,n]\)
\(H_{i} = b_{0} + b_{1} \left(\dfrac{y}{s} \right) +\left (\dfrac{y}{s} \right) ^{1+i} \)
Con \(i \in [1,m]\)
Sustituyendo dichas funciones en las condiciones de contorno (6 incógnitas, 6 condiciones) podemos obtener el valor de las constantes:
\(a_{0} = \dfrac{3EI}{ks^{3}} \cdot \dfrac{(3+i)\cdot (2+i)}{6} \\\) \(a_{1} = \dfrac{(3+i)(2+i)(ks^3-3EI) – 6ks^3}{6ks^{3}} \\\) \(a_{2} = 0 \\\) \(a_{3} = – \dfrac{(3+i)\cdot(2+i)}{6} \\\) \(b_{0} = -\dfrac{GJ(1+i)}{2kb^{2}s} \\\) \(b_{1} = -(1+i) \\\)Modelo aerodinámico
La solución temporal a dichas ecuaciones diferenciales debe ser una función exponencial compleja tal que:
\(W_{i}(t) = \bar{W_{i}} e^{\nu t}\)
\(A_{i}(t) = \bar{A_{i}} e^{\nu t}\)
Donde el exponente es un número complejo tal que:
\(\nu = \gamma + i \cdot \omega\)
Para definir el modelo aerodinámico y así poder resolver las ecuaciones, debemos emplear la aproximación de Theodorsen que define la sustentación y el momento aerodinámico en el eje elástico en el caso de que el movimiento fuera oscilatorio sin término de amortiguamiento (es decir, \(w = \bar{w} e^{i \cdot \omega}, \alpha= \bar{\alpha} e^{i \cdot \omega} \)) y usar dichos valores en el problema completo.
Los valores de sustentación y momento aerodinámico en el eje elástico según Theodorsen resultan:
\(l=\pi \rho_{\infty} b^{3} \omega^{2} [l_{w}(k) \cdot \dfrac{\bar{w}}{b} + l_{\alpha}(k) \bar{\alpha}] \\ \)
\(m_{ac}=\pi \rho_{\infty} b^{4} \omega^{2} [m_{w}(k)\cdot\dfrac{\bar{w}}{b} + m_{\alpha}(k) \bar{\alpha}]\\\)
Cuyos coeficientes se extraen directamente del libro de Hodges [Dewey H Hodges, G Alvin Pierce – Introduction to Structural Dynamics and Aeroelasticity 2011, página 216 ecuación 5.134]:
\(l_{w} = 1 – 2i\dfrac{C(k)}{k} \\ \) \(l_{\alpha} = a + \dfrac{i}{k} \left [1+2(1/2 + a) \cdot C(k) \right ] + \dfrac{2 \cdot C(k)}{k^{2}} \\\) \(m_{w} = a – \dfrac{2i(1/2+a) \cdot C(k)}{k} \\\) \(m_{\alpha} = a^{2} + \dfrac{1}{8} – \dfrac{(1/2-a)[1-2(1/2+a) \cdot C(k)] \cdot i}{k} + \dfrac{2(1/2 + a) \cdot C(k)}{k^{2}} \\\)Con la función de Theodorsen definida como:
\(C(k) = \dfrac{K_{1}(ik)}{K_{0}(ik)+K_{1}(ik)}\)
Donde \(K_{0},K_{1}\) son las Funciones de Bessel modificadas de segunda especie y \(k\) la frecuencia reducida.
Sustitución ecuaciones
Recordemos que las ecuaciones a sustituir son las siguientes:
\(EI \dfrac{\partial^{4} w (y,t)}{\partial y^{4}} + mg + m \dfrac{\partial ^{2} w (y,t)}{\partial t^{2}} – l = 0\)
\(GJ \dfrac{\partial ^{2} \alpha}{\partial y^{2}} + m_{ac} – i_{yG} \dfrac{\partial ^{2} \alpha}{\partial t^{2}} = 0 \)
Sustituyendo los grados de libertad por el sumatorio de funciones que hemos definido, el modelo aerodinámico por el modelo según Theodorsen e integrando las ecuaciones por cada uno de los modos de deformación (para así aplicar Galerkin correctamente y repartir el error) obtenemos las siguientes ecuaciones integrales:
\(\displaystyle \int_{0}^{s} \left [EI \sum_{j=1}^{n} F_{j}^{IV}\bar{W}_{j}+ mg + m \nu^{2} \sum_{j=1}^{n} F_{j} \bar{W}_{j} – \pi \rho_{\infty} b^{3} \omega^{2} \left ( l_{w} \sum_{j=1}^{n} F_{j} \dfrac{\bar{W}_{j}}{b} + l_{\alpha} \sum_{j=1}^{m} H_{j} \bar{A}_{j} \right ) \right ] \cdot F_{i} dy = 0 \\\)
\(\displaystyle \int_{0}^{s} \left [GJ \sum_{j=1}^{m} H_{j}^{II} \bar{A}_{j} – i_{yG} \nu^{2} \sum_{j=1}^{m} H_{j}\bar{A}_{j} + \pi \rho_{\infty} b^{4} \omega^{2} \left ( m_{w} \sum_{j=1}^{n} F_{j} \dfrac{\bar{W}_{j}}{b} + m_{\alpha} \sum_{j=1}^{m} H_{j} \bar{A}_{j} \right ) \right ] \cdot H_{i} dy = 0\)Hemos obtenido un sistema de n ecuaciones \((F_{1} \dots F_{n})\) + m ecuaciones \((H_{1} \dots H_{m})\) para los n+m grados de libertad \((W_{1} \dots W_{n}, A_{1} \dots A_{m})\) . Matricialmente es un sistema de ecuaciones tal que:
\( \left \{[A] \nu^{2} + [B] \right \} \cdot \left \{ \bar{q} \right \} = [C] \)
Donde \([C]\) representa la matriz de cargas externas (en este caso, el peso propio). Tendremos una solución particular + homogénea. El flameo se encuentra en la solución homogénea, por lo que podemos eliminar el peso propio para estudiar su comportamiento.
Por otra parte, se está integrando toda la placa de 0 a s. No obstante, un primer paso para adimensionalizar las ecuaciones es adimensionalizar la integración de forma que definimos una nueva variable de integración \(\psi = \dfrac{y}{s}\) tal que:
\(\dfrac{d^{n}}{dy^{n}} = \dfrac{1}{s^{n}} \cdot \dfrac{d^{n}}{d\psi ^{n}}\)
\(\displaystyle \int_{0}^{s} dy = s \cdot \int_{0}^{1} d\psi \)
Además, definimos los siguientes términos adimensionales:
\(\mu = \dfrac{m}{\pi \rho_{\infty} b^{2}}\)
\(r^{2} = \dfrac{i_{yG}}{m b^{2}}\)
\(\dfrac{GJ}{i_{yG} s^{2}} = \omega_{T}^{2}\)
\(\dfrac{EI}{ms^{4}} = \omega_{F}^{2} = \sigma^{2} \omega_{T}^{2}\)
\(\dfrac{b^{2} \omega_{T}^{2}}{U_{\infty}^{2}} = \dfrac{1}{V^{2}}\)
\(\dfrac{b^{2} \nu^{2}}{U_{\infty}^{2}} = p^{2}\)
\(\dfrac{b^{2} \omega^{2}}{U_{\infty}^{2}} = k^{2}\)
Adimensionalizando las ecuaciones empleando estas magnitudes adimensionales llegamos a las siguientes ecuaciones:
\(\displaystyle \int_{0}^{1} \left [\mu \cdot \sigma^{2} \cdot \omega_{T}^{2} \sum_{j=1}^{n} F_{j}^{IV} \dfrac{\bar{W}_{j}}{b} + \mu \cdot \nu^{2} \sum_{j=1}^{n} F_{j} \dfrac{\bar{W}_{j}}{b} – \omega^{2} l_{w} \sum_{j=1}^{n} F_{j} \dfrac{\bar{W}_{j}}{b} – \omega^{2} l_{\alpha} \sum_{j=1}^{m} H_{j} \bar{A}_{j} \right ] \cdot F_{i} d\psi = 0\) \(\displaystyle \int_{0}^{1} \left [\mu \cdot r^{2} \cdot \omega_{T}^{2} \sum_{j=1}^{m} H_{j}^{II} \bar{A}_{j} – \mu \cdot r^{2} \cdot \nu^{2} \sum_{j=1}^{m} H_{j}\bar{A}_{j} + \omega^{2} m_{w} \sum_{j=1}^{n} F_{j} \dfrac{\bar{W}_{j}}{b} +\omega^{2} m_{\alpha} \sum_{j=1}^{m} H_{j} \bar{A}_{j} \right ] \cdot H_{i} d\psi = 0\)Definiendo las integrales como:
\(\displaystyle I_{1}(i,j) = \int_{0}^{1} \left ( F_{j}^{IV} \cdot F_{i} \right ) d\psi \)
\(\displaystyle I_{2}(i,j) = \int_{0}^{1} \left ( F_{j} \cdot F_{i} \right ) d\psi \)
\(\displaystyle I_{3}(i,j) = \int_{0}^{1} \left ( H_{j} \cdot F_{i} \right ) d\psi \)
\(\displaystyle I_{4}(i,j) = \int_{0}^{1}\left ( H_{j}^{II} \cdot H_{i} \right ) d\psi \)
\(\displaystyle I_{5}(i,j) = \int_{0}^{1}\left ( H_{j} \cdot H_{i} \right ) d\psi \)
\(\displaystyle I_{6}(i,j) = \int_{0}^{1} \left ( F_{j} \cdot H_{i} \right ) d\psi \)
Multiplicando las ecuaciones por \(\dfrac{b^{2}}{U_{\infty}^{2}}\) y agrupando las integrales resulta el siguiente sistema matricial:
\(\left \{[MM] p^{2} + [KK] \dfrac{1}{V^{2}} + [AA] k^{2} \right \} \cdot \left \{ \bar{q} \right \} = 0\)
Con las matrices, de dimensiones {(n+m)x(n+m)} definidas como:
\([MM] = \begin{bmatrix} \mu \cdot I_{2}(1,1) & \dots & \mu \cdot I_{2}(1,n) & 0 & \dots & 0\\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots\\ \mu \cdot I_{2}(n,1) & \dots & \mu \cdot I_{2}(n,n) & 0 & \dots & 0\\ 0 & \dots & 0 & -\mu \cdot r^{2} \cdot I_{5}(1,1) & \dots & -\mu \cdot r^{2} \cdot I_{5}(1,m)\\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots\\ 0 & \dots & 0 & -\mu \cdot r^{2} \cdot I_{5}(m,1) & \dots & -\mu \cdot r^{2} \cdot I_{5}(m,m)\\ \end{bmatrix} \\\) \([KK] = \begin{bmatrix} \mu \cdot \sigma^{2} \cdot I_{1}(1,1) & \dots & \mu \cdot \sigma^{2} \cdot I_{1}(1,n) & 0 & \dots & 0\\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots\\ \mu \cdot \sigma^{2} \cdot I_{1}(n,1) & \dots & \mu \cdot \sigma^{2} \cdot I_{1}(n,n) & 0 & \dots & 0\\ 0 & \dots & 0 & \mu \cdot r^{2} \cdot I_{4}(1,1) & \dots & \mu \cdot r^{2} \cdot I_{4}(1,m)\\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots\\ 0 & \dots & 0 & \mu \cdot r^{2} \cdot I_{4}(m,1) & \dots & \mu \cdot r^{2} \cdot I_{4}(m,m)\\ \end{bmatrix} \\\) \([AA] = \begin{bmatrix} -l_{w} \cdot I_{2}(1,1) & \dots & -l_{w} \cdot I_{2}(1,n) & -l_{\alpha} \cdot I_{3}(1,1) & \dots & -l_{\alpha} \cdot I_{3}(1,m)\\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots\\ -l_{w} \cdot I_{2}(n,1) & \dots & -l_{w} \cdot I_{2}(n,n) & -l_{\alpha} \cdot I_{3}(n,1) & \dots & -l_{\alpha} \cdot I_{3}(n,m)\\ m_{w} \cdot I_{6}(1,1) & \dots & m_{w} \cdot I_{6}(1,n) & m_{\alpha} \cdot I_{5}(1,1) & \dots & m_{\alpha} \cdot I_{5}(1,m)\\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots\\ m_{w} \cdot I_{6}(m,1) & \dots & m_{w} \cdot I_{6}(m,n) & m_{\alpha} \cdot I_{5}(m,1) & \dots & m_{\alpha} \cdot I_{5}(m,m)\\ \end{bmatrix} \\\)Para encontrar una solución a la frecuencia compleja adimensional debemos hacer el determinante nulo, es decir:
\(\| [MM] p^{2} + [KK] \dfrac{1}{V^{2}} + [AA] k^{2} \| = 0\)
Lo cual es un problema de autovalores generalizados de la forma:
\(\boxed{\| [A] – \lambda [B] \| = 0}\) con \(\sqrt{\lambda} = p\), \([A]= [KK] \dfrac{1}{V^{2}} + [AA] k^{2}\) y \([B]= -[MM] \)
Es decir, estamos interesados en obtener los valores de la frecuencia compleja adimensional \(p = g + i \cdot k\) que hacen el determinante nulo. No obstante, el determinante también depende de la velocidad adimensional \(V\) y de la propia frecuencia reducida \(k\). Para resolver el problema emplearemos el método p-k siguiendo el siguiente procedimiento:
- Se hace un barrido de la velocidad adimensional. Para cada \(V\):
- Se hace un barrido de diferentes valores de \(k\)
- Para cada valor de k se resuelve el problema de autovalores generalizados y obtenemos \(\lambda \rightarrow p\)
- Sólo son válidas las soluciones en las que la parte imaginaria de \(p\) coinciden con el \(k\) barrido para que la solución sea coherente con la definición de fuerzas aerodinámicas.
- Para cada \(V\) hay asociadas tantas soluciones \(p\) como modos de deformación considerados, teniendo una parte compleja y una parte real.
- La primera velocidad dimensional \(U_{\infty}\) para la cual se tiene \(Re(p) > 0\) es la velocidad de flameo.
- En dicho punto obtenemos la frecuencia reducida de flameo \(k_{F}\), la velocidad de flameo \(U_{F}\) y la frecuencia de flameo \(\omega_{F}\)
Solución
Solución primer apartado
1 Función de aproximación para flexión/torsión
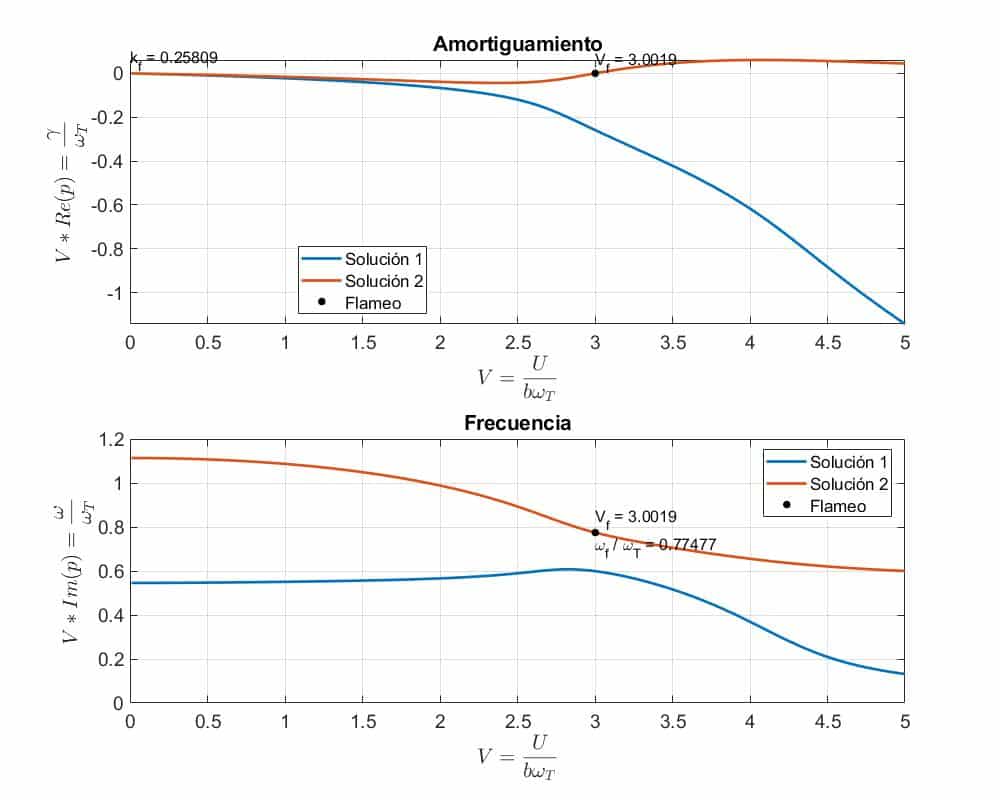
La velocidad de flameo es = 23.288289 m/s
La frecuencia de flameo es = 12.021141 rad/s
5 Funciones de aproximación para flexión/torsión
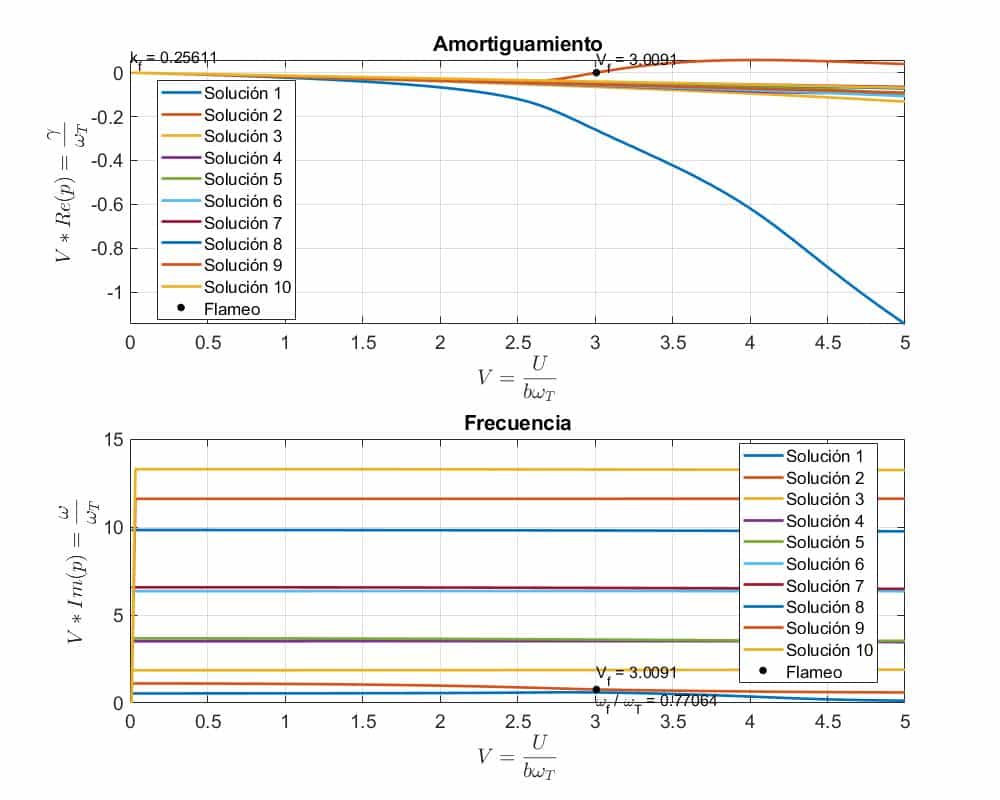
La velocidad de flameo es = 23.344114 m/s
La frecuencia de flameo es = 11.957095 rad/s
Solución segundo apartado
Para resolver este apartado se usa la lógica: con muelles de infinita rigidez el problema se resumiría al de un ala empotrada. En dicho caso, la solución sería la que se muestra a continuación:
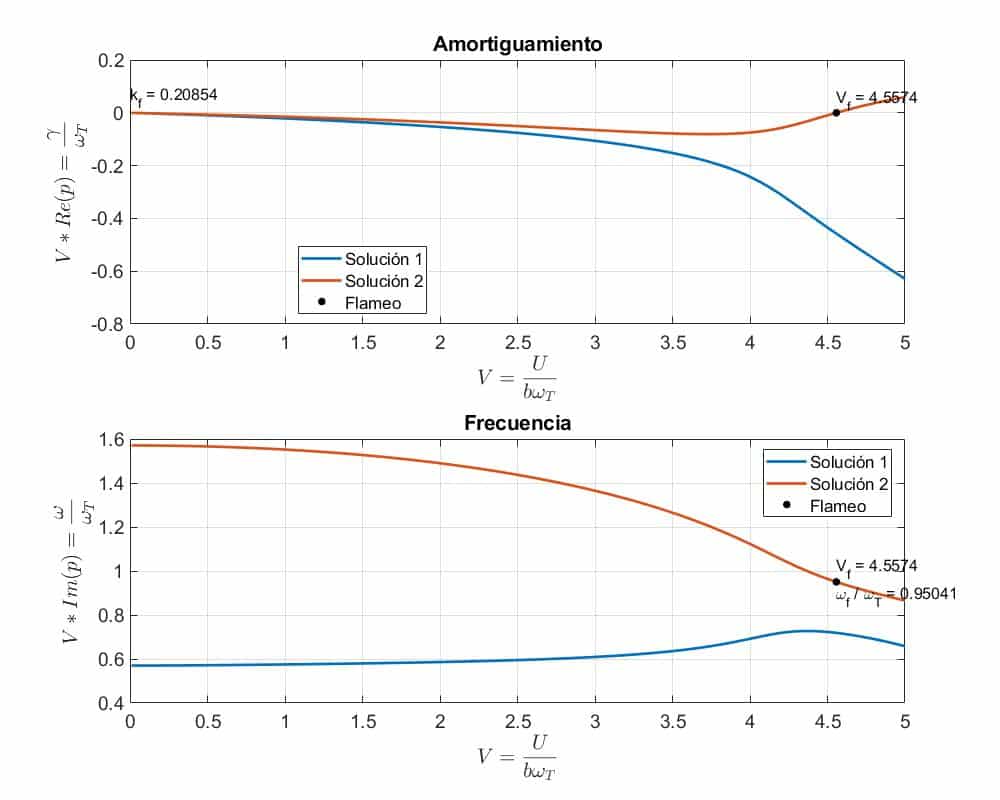
Es decir, se obtendría una velocidad de flameo de 35.355709 m/s y una frecuencia de flameo de 14.746335 rad/s.
Dicha velocidad es un 51.82% superior con respecto a la velocidad en el problema inicial empleando 1 función de aproximación. Dada la similitud con lo que se propone en el último apartado y teniendo en cuenta que la solución es aproximada, se supone que el límite estaría alrededor del 50%.
A continuación se muestra el cálculo de la velocidad y frecuencia de flameo para diferentes valores de rigidez donde puede observarse claramente cómo se encuentra una asíntota al aumentar la rigidez de los muelles y el resultado tiende a lo obtenido con el ala empotrada:
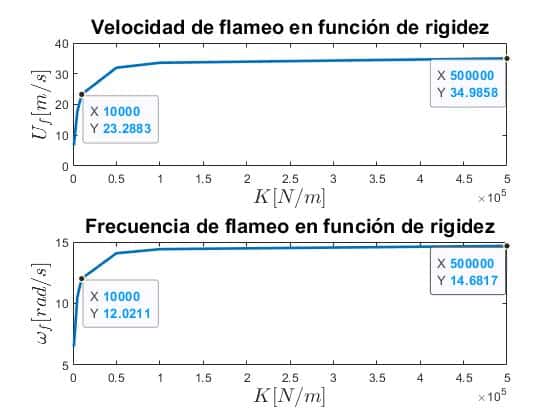
Código de MATLAB
A continuación se presenta el código de MATLAB empleado para resolver el problema del flameo en base a las ecuaciones expuestas en este artículo para un número indefinido de funciones de aproximación (bastaría cambiar los valores de m y n):
%%% Metodo PK en ala continua
clear all
clc
close all
%% INICIALIZACIÓN
% Datos
a=0;
% Características de la placa
b=0.5;
s=4;
t=0.01;
rho=2700;
E=70.5e9;
E=68.9e9;
G=26e9;
I=(2*b)*t^3/12;
J=1/3*2*b*t^3;
m=2*b*t*rho;
igy=(m*(2*b)^2)/12;
%Características del problema
rhoinf=1.225;
K=10000;
%Parámetros adimensionales
mu=m/(pi*rhoinf*b^2);
r=sqrt(igy/(m*b^2));
wf=sqrt(E*I/(m*s^4));
wt=sqrt(G*J/(igy*s^2));
sigma=wf/wt;
%% Funciones de aproximación
%Funciones y sus derivadas con respecto a y, expresando phi=y/s
nn=1; %n funciones aproximacion flexion
nm=1; %m funciones aproximacion torsion
a0=@(i) (3*E*I/(K*s^3))*(3+i)*(2+i)/6;
a1=@(i) ((3+i)*(2+i)*(K*s^3-3*E*I)-(6*K*s^3))/(6*K*s^3);
a2=0;
a3=@(i) -((3+i)*(2+i))/6;
%Flexión
F = @(phi,i) a0(i) + a1(i).*phi + a2.*phi.^2 + a3(i).*phi.^3 + phi.^(3+i);
F_I = @(phi,i) a1(i) + 2*a2.*phi + 3*a3(i).*phi.^2 + (3+i)*phi.^(2+i); %Primera derivada
F_II = @(phi,i) 2*a2 + 6*a3(i).*phi + (3+i)*(2+i)*phi.^(1+i); %Segunda derivada
F_III = @(phi,i) 6*a3(i) + (3+i)*(2+i)*(1+i)*phi.^(i); %Tercera derivada
F_IV = @(phi,i) (3+i)*(2+i)*(1+i)*i*phi.^(i-1); %Cuarta derivada
b1=@(i) -(1+i);
b0=@(i) -(G*J/(2*K*b^2*s))*(1+i);
%Torsión
H = @(phi,i) b0(i) + b1(i).*phi + phi.^(1+i);
H_I = @(phi,i) b1(i) + (1+i)*phi; %Primera derivada
H_II = @(phi,i) (i+1).*i.*phi.^(i-1); %Segunda derivada
%% Comprueba que las funciones de aproximación cumplen
%Las condiciones de contorno del problema
%Comprueba flexión
residuof=0;
for i=1:nm
residuof=residuof+abs(F_II(0,i));
residuof=residuof+abs(F_II(1,i));
residuof=residuof+abs(s^3*F(0,i)+(E*I)/(2*K)*F_III(0,i));
residuof=residuof+abs(F(1,i));
end
%residuof
%Comprueba flexión
residuot=0;
for i=1:nm
residuot=residuot+abs(s*H(0,i)-(G*J)/(2*K*b^2)*H_I(0,i));
residuot=residuot+abs(H_I(1,i));
end
%residuot
%% Calcula las integrales
for i=1:nn
for j=1:nn
I1(i,j)=quadgk(@(phi) F(phi,i).*F_IV(phi,j),0,1);
end
end
for i=1:nn
for j=1:nn
I2(i,j)=quadgk(@(phi) F(phi,i).*F(phi,j),0,1);
end
end
for i=1:nn
for j=1:nm
I3(i,j)=quadgk(@(phi) F(phi,i).*H(phi,j),0,1);
end
end
for i=1:nm
for j=1:nm
I4(i,j)=quadgk(@(phi) H(phi,i).*H_II(phi,j),0,1);
end
end
for i=1:nm
for j=1:nm
I5(i,j)=quadgk(@(phi) H(phi,i).*H(phi,j),0,1);
end
end
for i=1:nm
for j=1:nn
I6(i,j)=quadgk(@(phi) F(phi,j).*H(phi,i),0,1);
end
end
%% Cálculo de cortes
%Matriz de MASA/INERCIA (no depende de k ni V)
for i=1:nn
for j=1:nn
MM1(i,j)=mu*I2(i,j);
end
end
for i=1:nn
for j=1:nm
MM2(i,j)=0;
end
end
for i=1:nm
for j=1:nn
MM3(i,j)=0;
end
end
for i=1:nm
for j=1:nm
MM4(i,j)=-r^2*mu*I5(i,j);
end
end
MM=[MM1,MM2;MM3,MM4];
% Genera valores para recorrer
VV=linspace(0.01,5,200); % Velocidades adimensionales del fluido
kk=logspace(-4,3,500); % Rango de frecuencias reducidas (muchas cercanas al 0-1)
%
%Recorre cada velocidad adimensional
for i=1:length(VV)
V=VV(i);
%Recorre cada frecuencia
for j=1:length(kk)
k=kk(j);
%Cálculo aerodinámica
C = besselk(1,1i*k)/(besselk(0,1i*k)+besselk(1,1i*k)); % Función de Theodorsen
k2lw = k^2 * (1-2.*1i.*C/k); % k^2 * lw en C
k2la = k^2 * (a+(1i/k).*(1+2.*(0.5-a).*C)+2.*C./k.^2); % k^2 * la en C
k2mw = k^2 * (a-(2.*1i.*(0.5+a).*C)./k); % k^2 * mw en C
k2ma = k^2 * (a^2+1/8-((0.5-a)*(1-2*(0.5+a)*C))*1i/k+(2*(0.5+a)*C)/k^2); % k^2 * ma en C
%Matriz de rigidez
for z=1:nn
for x=1:nn
KK1(z,x)=sigma^2*mu*I1(z,x)/V^2;
end
end
for z=1:nn
for x=1:nm
KK2(z,x)=0;
end
end
for z=1:nm
for x=1:nn
KK3(z,x)=0;
end
end
for z=1:nm
for x=1:nm
KK4(z,x)=mu*r^2*I4(z,x)/V^2;
end
end
KK=[KK1,KK2;KK3,KK4];
%Matriz aerodinámica
for z=1:nn
for x=1:nn
AA1(z,x)=-k2lw*I2(z,x);
end
end
for z=1:nn
for x=1:nm
AA2(z,x)=-k2la*I3(z,x);
end
end
for z=1:nm
for x=1:nn
AA3(z,x)=k2mw*I6(z,x);
end
end
for z=1:nm
for x=1:nm
AA4(z,x)=k2ma*I5(z,x);
end
end
AA=[AA1,AA2;AA3,AA4];
% Determinante a resolver
% | MM*p^2 + KK + AA | = 0
% Lo cual se puede expresar como un problema de autovalores
% | (KK + AA) -lambda*(-MM) | = 0 -> lambda=p^2
A=KK+AA;
B=-MM;
lambdas=eig(A,B);
p(j,:)=sqrt(lambdas);
%Tomo la solución con parte imaginaria positiva
for f=1:(nn+nm)
if imag(p(j,f))<0
p(j,f)=-p(j,f);
end
end
%Ordeno las soluciones
ptemp = -1i*p(j,:); % Cambiar parte imaginaria por compleja para ordenar
ptemp = sort(ptemp,'ComparisonMethod','real'); % Ordeno los valores según k (parte imag de p)
p(j,:) = 1i*ptemp; %Vuelvo a generar el vector pero ordenado
end
%Intersección de k con las soluciones p
%En psol defino las soluciones para cada velocidad
for f=1:(nn+nm) %para cada solucion preliminar
for j = 1:(length(kk) - 1)
k = kk(j);
kmas1 = kk(j+1);
if (imag(p(j,f)) - kk(j))*(imag(p(j+1,f)) - kk(j+1)) < 0 %Hay corte con k
psol(i,f) = p(j,f) - (p(j+1,f) - p(j,f))*(imag(p(j,f))-kk(j))/(imag(p(j+1,f)) - kk(j+1) - imag(p(j,f)) + kk(j));
break
end
end
end
end
% Ya están todas las soluciones de p para cada velocidad adimensional V
% %% Buscamos punto de flameo
Vf=1e5; %Toma valor inicial alto
for i=1:length(VV)-1
V=VV(i);
%Mira si en alguna solucion la parte real se anula
%Sólo recorre la longitud de psol porque a veces no siempre
%converge k
for f=1:length(psol(i,:)) %para cada solucion válida
if real(psol(i,f))*real(psol(i+1,f))<0 %Cambia el signo, Bolzano
V_candidato(f)=VV(i) - real(psol(i,f))*(VV(i+1) - VV(i))/(real(psol(i+1,f))-real(psol(i,f)));
k_candidato(f)=imag(psol(i,f)) - real(psol(i,f))*(imag(psol(i+1,f)) - imag(psol(i,f)))/(real(psol(i+1,f)) - real(psol(i,f)));
if V_candidato(f) < Vf
Vf = V_candidato(f);
kf = k_candidato(f);
end
end
end
end
%% Representación de solución
figure
subplot(2,1,1)
plot(VV,VV(:).*real(psol(:,1)),'DisplayName','Solución 1','LineWidth',2)
hold on
for f=2:length(psol(1,:))
plot(VV,VV(:).*real(psol(:,f)),'DisplayName',sprintf('Solución %d',f),'LineWidth',2)
end
title('Amortiguamiento','FontSize',15)
xlabel('$\displaystyle V = \frac{U}{b \omega_{T}}$','interpreter','latex','FontSize',15)
ylabel('$\displaystyle V*Re(p) = \frac{\gamma}{\omega_{T}}$','interpreter','latex','FontSize',15)
grid on
legend('Location','Best')
if Vf<10
plot(Vf,0,'ok','DisplayName','Flameo','Markersize',5,'MarkerFaceColor','k')
text(Vf,0.05,{['V_f = ',num2str(Vf)]},'FontSize', 12);
end
set(gca,'FontSize',14)
if Vf<10
ylim=get(gca,'ylim');
xlim=get(gca,'xlim');
text(xlim(1),ylim(2),{['k_f = ',num2str(kf)]},'FontSize', 12)
end
subplot(2,1,2)
plot(VV,VV(:).*imag(psol(:,1)),'DisplayName','Solución 1','LineWidth',2)
hold on
for f=2:length(psol(1,:))
plot(VV,VV(:).*imag(psol(:,f)),'DisplayName',sprintf('Solución %d',f),'LineWidth',2)
end
title('Frecuencia','FontSize',15)
xlabel('$\displaystyle V = \frac{U}{b \omega_{T}}$','interpreter','latex','FontSize',15)
ylabel('$\displaystyle V*Im(p) = \frac{\omega}{\omega_{T}}$','interpreter','latex','FontSize',15)
grid on
legend('Location','Best')
%ylim([0 3])
if Vf<10
plot(Vf,Vf*kf,'ok','DisplayName','Flameo','Markersize',5,'MarkerFaceColor','k')
text(Vf,Vf*kf,{['V_f = ',num2str(Vf)];['\omega_f / \omega_T = ',num2str(Vf*kf)]},'FontSize', 12);
end
set(gca,'FontSize',14)
%set(gcf, 'Position', [200, 200, 1000, 800])
fprintf('La velocidad de flameo es = %f m/s \n',Vf*b*wt);
fprintf('La frecuencia de flameo es = %f rad/s \n',Vf*kf*wt);

![Examen Matemáticas Andalucía Junio 2023 Resuelto Selectividad [PEvAU] MatematicasII_1](https://ingenieriabasica.es/wp-content/uploads/2023/07/MatematicasII_1-143x200.jpg)

Uy hombre! mis respetos, ese código de Mathlab es una mier…he estado viendo a Galerkin todo el mes con elementos finitos y ya me espanta…
Jajajjajaja es un código complejo pero funciona bastante bien 🙂