En este artículo se presenta la solución detallada paso por paso del examen de Matemáticas II que cayó en Junio de 2023 en Andalucía en Selectividad (PEvAU).
Enunciado


Ejercicio 1
Considera la función \(f: \mathbb{R} \rightarrow \mathbb{R}\) definida por \(f(x) = \dfrac{1}{e^{x} + e^{-x}}\)
Apartado a)
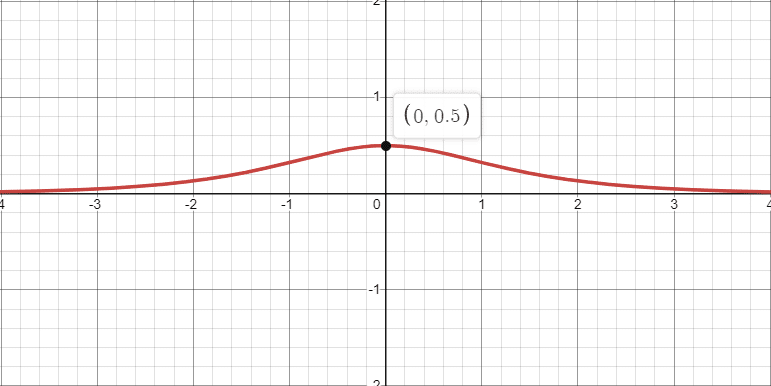
Estudia y halla los máximos y mínimos absolutos de \(f\) (abcisas donde se obtienen y valores que se alcanzan)
Para este primer apartado de cálculo de límites es necesario calcular la derivada de la función e igualar a 0 para obtener los mínimos y máximos.
\(\dfrac{d}{dx} \left ( \dfrac{1}{e^{x} + e^{-x}} \right ) = – \dfrac{e^{x} – e^{-x}}{(e^{x} + e^{-x})^{2}} = 0 \iff e^{x} – e^{-x} = 0 \)Esta igualdad sólo se cumple para \(x=0\). Si calculamos su derivada segunda para observar el signo:
\(\dfrac{d^{2}}{dx^{2}} \left ( \dfrac{1}{e^{x} + e^{-x}} \right ) = – \dfrac{(e^{x} + e^{-x})^{3}+ 2 (e^{x} – e^{-x})^{2} (e^{x} + e^{-x})}{(e^{x} + e^{-x})^{4}}\) \(f»(0) = – \dfrac{2^{3}}{2^{4}} = – \dfrac{1}{2}\)Por lo tanto, el único extremo de esta función es un máximo al ser la segunda derivada negativa. Sustituyendo en la función original:
\(\boxed{f(0) = \dfrac{1}{2}}\)
Como la función no está acotada y tiende a 0 para \(\pm \infty\), siendo positiva en todo el intervalo de los números reales al ser tanto numerador como denominador siempre positivos, el único extremo es un máximo absoluto en \((0 , \dfrac{1}{2})\)
Apartado b)
\(\lim_{x\to\infty} \dfrac{x^{2}}{e^{x} + e^{-x}} = \dfrac{\infty}{\infty}\)Calcula \(\lim_{x\to\infty} (x^{2} f(x))\)
Como el límite es indeterminado, aplicamos la regla de l’Hôpital:
\(\lim_{x\to\infty} \dfrac{x^{2}}{e^{x} + e^{-x}} = \dfrac{\infty}{\infty} =\) \( \lim_{x\to\infty} \dfrac{2x}{e^{x} – e^{-x}} = \dfrac{\infty}{\infty} = \) \( \lim_{x\to\infty} \dfrac{2}{e^{x} + e^{-x}} = \dfrac{2}{\infty} = 0\)Por lo tanto, \(\boxed{\lim_{x\to\infty} (x^{2} f(x)) = 0}\)
Ejercicio 2
Sea la función \(f : [-2,2] \rightarrow \mathbb{R}\), definida por \(f(x) = x^{3} – 2x + 5\)
Apartado a)
Determina las abscisas de los puntos, si existen, en los que la pendiente de la recta tangente coincide con la pendiente de la recta que pasa por los puntos \((-2,f(-2))\) y \((2,f(2))\)
En primer lugar obtenemos el valor de la función en los puntos pedidos:
\(f(-2) = 1\) \(f(2) = 9\)Por lo tanto, la recta es la determinada por los puntos (-2,1) y (2,9). Esta recta tiene como pendiente \(m= \dfrac{9-1}{2+2} = 2\)
La derivada de una función en un punto da como valor la pendiente de la recta tangente en dicho punto. Por lo tanto, hay que buscar el valor de \(x\) tal que \(f'(x) = 2\)
\(f'(x) = 3x^{2} – 2 = 2 \iff \boxed{x = \pm \dfrac{2}{\sqrt{3}}}\)Se tiene además que \(\pm \dfrac{2}{\sqrt{3}} \approx \pm 1.15\), que está dentro del dominio, siendo por lo tanto la solución válida.
Apartado b)
Determina la ecuación de la recta tangente y la ecuación de la recta normal a la gráfica de \(f\) en el punto de inflexión
El punto de inflexión se encuentra cuando la derivada segunda se anula, es decir, buscamos la \(x\) tal que \(f»(x) = 0\)
\(f»(x) = 6x = 0 \iff x=0\)Además, siendo \(f(0) = 5\), podemos afirmar que el punto de inflexión se encuentra en el (0,5)
La recta tangente será una recta que pase por dicho punto de pendiente \(m = f'(0) = -2\)
La recta normal será una recta que pase por dicho punto y normal a su tangente, es decir, de pendiente \(m ‘= – \dfrac{1}{m} = \dfrac{1}{2}\)
Como la fórmula de una recta en un sistema de coordenadas x-y se define como: \(y=m(x-x_{0}) + y_{0}\), la solución pedida es:
- Recta tangente: \(\boxed{y = -2x + 5}\)
- Recta normal: \(\boxed{y = \dfrac{1}{2}x + 5}\)
Ejercicio 3
Considera la función \(f: \mathbb{R} \rightarrow \mathbb{R}\) definida por \(f(x) = x |x-1|\). Calcula el área del recinto limitado por la gráfica de dicha función y su recta tangente en el punto de abcisa x=0
Antes de nada, para comprender mejor la función hay que definir su valor por tramos. La función a analizar se define como:
\(f(x) = \begin{cases} -x^{2} + x & \quad x \leq 1 \\ x^{2} -x & \quad x \geq 1 \\ \end{cases}\) \(f'(x) = \begin{cases} -2x + 1 & \quad x \leq 1 \\ 2x – 1 & \quad x \geq 1 \\ \end{cases}\)En \(f(x=0) = 0\) la recta tangente tiene como pendiente \(f'(0) = 1\)
Como la ecuación de dicha recta tangente de pendiente unidad que pasa por el origen es \(y=x\), los puntos de corte de dicha recta tangente con la gráfica de la función, que son los que delimitan el recinto sobre el cuál calcular el área (por medio de una integral), son aquellos puntos en los que \(f(x) = x\)
Para \(x \leq 1 \rightarrow -x^{2} + x = x \iff x=0\)
Para \(x \geq 1 \rightarrow x^{2} – x = x \iff x=2\)
Obsérvese que, para el segundo caso, la ecuación daría también como solución \(x=0\). No obstante, se consideran valores tal que \(x \geq 1 \), así que cuidado porque no sería válido
Las áreas a calcular serían las siguientes:
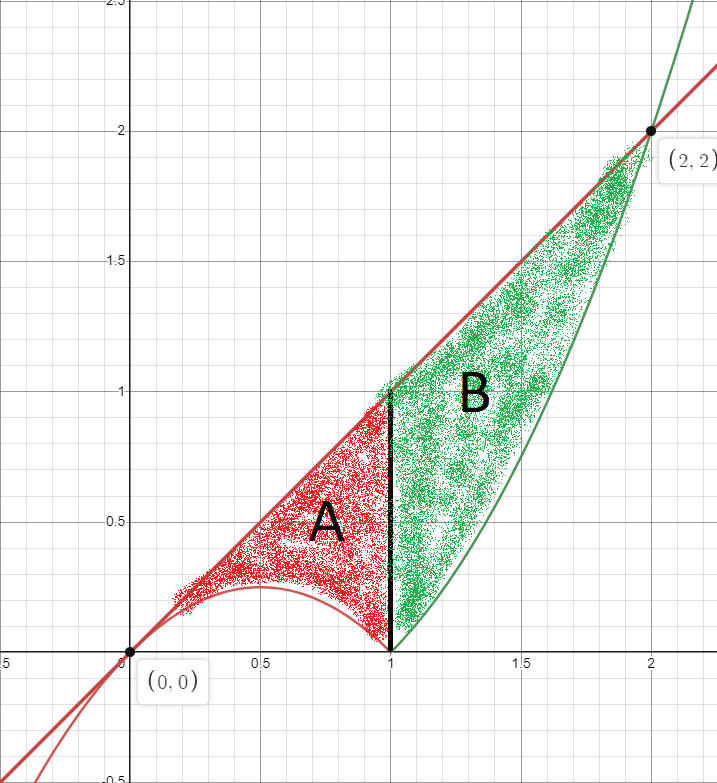
El área total sería T = A + B. He hecho la separación de las áreas porque genera menos lío y, de lo contrario, habría que dividir la integral debido al cambio de función en x=1.
\(\displaystyle A = \int_{0}^{1} \left (x – (-x^{2} + x) \right ) dx = \int_{0}^{1} \left ( x^{2} \right ) dx = \dfrac{1}{3}\) \(\displaystyle B = \int_{1}^{2} \left (x – (x^{2} – x) \right ) dx = \int_{1}^{2} \left ( -x^{2} + 2x \right ) dx = \dfrac{2}{3}\)Por lo tanto, se tiene que el área es \(\boxed{T = A + B = 1 \ u^{2}}\)
Ejercicio 4
Considera la función \(F: \mathbb{R} \rightarrow \mathbb{R}\) definida por \(\displaystyle F(x) =\int_{0}^{x} sen(t^{2}) dt\). Calcula \(\lim_{x\to 0} \dfrac{x F(x)}{sen(x^{2})}\)
Para este ejercicio hay que tener claro el Teorema fundamental del cálculo, es decir, que la derivación e integración de una función son operaciones inversas. Siendo la función del enunciado definida como \(F(x) = \int_{0}^{x} f(t) dt\), se tiene que \(F'(x) = f(t=x) = sen(x^{2})\)
Por otra parte, para luego sustituir, se tiene que
\(f'(x) =2x \cos(x^{2})\)Si intentamos calcular el límite llegamos a:
\(\lim_{x\to 0} \dfrac{x F(x)}{sen(x^{2})} = \dfrac{0}{0}\)Por lo tanto, debemos aplicar la regla de l’Hôpital:
\(\lim_{x\to 0} \dfrac{x F(x)}{sen(x^{2})} = \dfrac{0}{0} =\) \(\lim_{x\to 0} \dfrac{F(x)+ xf(x)}{2x \cos(x^{2})} = \dfrac{0}{0} =\) \(\lim_{x\to 0} \dfrac{f(x)+ f(x) + xf'(x)}{2 \cos(x^{2}) – 4x^{2} sen(x^{2})} = \dfrac{0}{2} = 0\)Siendo por lo tanto el resultado \(\boxed{\lim_{x\to 0} \dfrac{x F(x)}{sen(x^{2})} = 0}\)
Ejercicio 5
Una marca de vehículos ha vendido este mes coches de tres colores: blancos, negros y rojos. El 60% de los coches blancos más el 50% de los coches negros representan el 30% de los coches vendidos. El 20% de los coches blancos junto con el 60% de los coches negros y el 60% de los coches rojos representan la mitad de los coches vendidos. Se han vendido 100 coches negros más que blancos. Determina el número de coches vendidos de cada color
Este ejercicio es extremadamente fácil y nadie que aspire a entrar a una carrera técnica lo debería de haber fallado. Asignando Blancos -> B, Negros -> N y Rojos ->R, el sistema de ecuaciones bruto sería:
- \(0,6B + 0,5N = 0,3 \cdot (B + N + R)\)
- \(0,2B + 0,6N + 0,6R = 0,5 \cdot (B + N + R)\)
- \(N = B + 100\)
Reescribiendo las ecuaciones y ordenandolas:
- \(0,3B + 0,2N – 0,3R = 0\)
- \(-0,3B + 0,1N + 0,1R = 0\)
- \(1B – 1N+ 0R = -100\)
El sistema se podría resolver manualmente por sustitución, por reducción, de manera matricial… E incluso luego se podría comprobar la solución con la calculadora. Por ejemplo, sustituyendo la última ecuación en las dos primeras:
- \(0,3B + 0,2 (B + 100) – 0,3R = 0 \rightarrow 0,5B – 0,3R + 20 = 0\)
- \(-0,3B + 0,1(B + 100) + 0,1R = 0 \rightarrow -0,2B + 0,1R + 10 = 0\)
Si multiplicamos la tercera por 3, las ecuaciones resultan:
- \(0,5B – 0,3R + 20 = 0\)
- \(-0,6B + 0,3R + 30 = 0\)
Si sumamos las ecuaciones:
\(-0,1B + 50 = 0 \rightarrow \boxed{B = 500}\)Por lo tanto:
\(\boxed{N = 600}\)Y despejando R de cualquiera de las últimas ecuaciones:
\(\boxed{R = 900}\)Ejercicio 6
Considera las matrices \(A = \begin{pmatrix} 0&0 &m \\ m&0 &0 \\0 & m&0 \end{pmatrix}\) y \(B = \begin{pmatrix} 1&0 &0 \\ 0&0 &1 \\0 & 1&0 \end{pmatrix}\)
Apartado a)
Determina para qué valores de \(m\) existe la inversa de la matriz A
La inversa de una matriz se define como:
\(M^{-1} = \dfrac{(Adj(M))^{T}}{|M|}\)
Por lo tanto, para que una matriz tenga inversa, debe de tener determinante distinto de 0. Hay que buscar los valores de m tal que el determinante de A sea distinto de 0.
\(\det(A) = \begin{vmatrix} 0&0 &m \\ m&0 &0 \\0 & m&0 \end{vmatrix} = m^{3} = 0 \iff m=0\)Por lo tanto, existe la inversa de la matriz A siempre que \(\boxed{m \neq 0}\)
Apartado b)
Para todo \(m \neq -1\), resuelve, si es posible, la ecuación \(AX + X = B\)
En este caso, la ecuación a resolver sería \((A+I)X = B \rightarrow X = (A+I)^{-1} B\)
Siendo necesario calcular la inversa de (A+I) y multiplicarla por la matriz B para obtener la solución.
La inversa de una matriz se define como:
\(M^{-1} = \dfrac{(Adj(M))^{T}}{|M|}\)
La matriz que queremos invertir es:
\(A+I = \begin{bmatrix} 1&0 &m \\ m&1 &0 \\0 & m&1 \end{bmatrix}\)Su determinante es:
\(det(A+I) = \begin{vmatrix} 1&0 &m \\ m&1 &0 \\0 & m&1 \end{vmatrix} = 1+ m^{3}\)Por lo tanto, queda patente que dicha matriz tiene inversa excepto si \(m=-1\), por eso nos lo aclaran en el enunciado. La matriz adjunta resulta:
\(Adj(A+I) = \begin{bmatrix} 1& -m &m^{2} \\ m^{2}&1 &-m \\-m & m^{2} &1 \end{bmatrix}\)La inversa resulta por lo tanto:
\((A+I)^{-1} = \dfrac{1}{1+m^{3}} \begin{bmatrix} 1& m^{2} & -m \\ -m &1 & m^{2} \\ m^{2} & -m&1 \end{bmatrix}\)Multiplicando las matrices, la solución resulta finalmente:
\(\boxed{X = (A+I)^{-1} B = \dfrac{1}{1+m^{3}} \begin{bmatrix} 1& -m &m^{2} \\ -m&m^{2} &1 \\m^{2} & 1& -m \end{bmatrix}}\)
Ejercicio 7
El plano perpendicular al segmento de extremos P(0,3,8) y Q(2,1,6) que pasa por su punto medio corta a los ejes coordenados en los puntos A, B y C. Halla el área del triángulo cuyos vértices son los puntos A, B y C.
Este ejercicio de geometría se podría resolver empleando fórmulas y algoritmos memorizados previamente. No obstante, fui capaz de resolverlo únicamente sabiendo la definición de un plano.
En la primera parte del ejercicios se nos pide calcular un plano dada una serie de restricciones. En primer lugar nos dicen que el plano es perpendicular a un determinado segmento. La ecuación de un plano \(\pi \) se define como:
\(\pi = Ex + Fy + Gz + D = 0 \), donde \(E, F \ y \ G\) es un vector perpendicular al plano y \(D\) es una constante que define la posición del plano a lo largo de dicho eje perpendicular que lo define.
Del enunciado, sabemos que el vector perpendicular es:
\((E,F,G) = \vec{PQ} = (2,1,6) – (0,3,8) = (2,-2,-2) = (1,-1,-1)\)
Obsérvese que he dividido los componentes porque nos interesa su dirección, no su magnitud; su magnitud se verá «regulada» posteriormente por la constante \(D\).
Nos dicen que el plano pasa por el punto medio de dicho segmento. Por lo tanto, dicho punto debe estar contenido en el plano. El punto medio es:
\(R = P + \dfrac{\vec{PQ}}{2} = (0,3,8) + (1,-1,-1) = (1,2,7)\)
Con dicha información, podemos fijar la posición del plano resolviendo la ecuación:
\(\pi = 1 \cdot 1 -1 \cdot 2 -1 \cdot 7 + D = 0 \rightarrow D = 8 \)
Por lo tanto, la ecuación del plano es:
\(\pi = x -y -z + 8 = 0\)
Para saber en qué puntos corta a los ejes coordenados, sustituimos los valores:
- Corte eje x -> A = (x,0,0)= -> \(x + 8 = 0\) -> A = (-8,0,0)
- Corte eje y -> B = (0,y,0)= -> \(-y + 8 = 0\) -> B = (0,8,0)
- Corte eje z -> C = (0,0,z)= -> \(-z + 8 = 0\) -> C = (0,0,8)
En este caso resulta un triángulo equilátero muy sencillo que se puede calcular a mano a lo «bruto», pero quiero hacer un desarrollo de cómo se calcularía cualquier triángulo.
Está claro que el área de un triángulo es base por altura dividido entre 2. Si tomamos por ejemplo como base el vértice que une A y B, tendríamos el segmento:
\(\overline{AB} = (8,8,0)\)
Cuya longitud es \(|\overline{AB}| = \sqrt{128} = 8 \sqrt{2} \ u\)
Necesitamos entonces ahora saber la altura del triángulo. Más de lo mismo; al ser equilátero sería el segmento formado por el punto C y el punto medio de la base, pero vamos al caso genérico. El segmento que define la altura pasaría obviamente por el punto C y estaría contenido en un plano definido por el vector de la base.
En primer lugar, al ser el vector (8,8,0) -> (1,1,0), el plano sería:
\(\pi = x + y + H = 0\)
Como debe contener al punto C, la constante resultaría:
\(\pi = 0 + 0 + H = 0 \rightarrow H=0\)
Por lo tanto, el plano que contiene a dicho segmento vendría definido por:
\(x+y= 0 \)
Para saber en qué punto cortaría al segmento \(\overline{AB}\), tendríamos que definir un vector para propagar la dirección hasta que cumpliese la ecuación del plano. Es decir, si parametrizamos el vector de forma:
- x = -8 + m
- y = m
- z = 0
Para m=0 estaríamos en el (-8,0,0) que sería el punto A, y para m = 8 estaríamos en el (0,8,0) que sería el punto B. Sustituyendo dicha parametrización en la ecuación del plano:
\((-8+m)+(m)= 0 \iff m=4\)
Es decir, que el punto sobre el que corta al segmento sería J = (-4,4,0), que no es más que el punto medio entre A y B como se comentó anteriormente. La altura del triángulo sería por lo tanto la longitud del segmento \(\overline{CJ} = |(4,-4,8)| = \sqrt{16 + 16 + 64} = 4 \sqrt{6} \ u\)
El área sería:
\(\boxed{\dfrac{4 \sqrt{6} \cdot 8 \sqrt{2}}{2} = 32 \sqrt{3} \ u^{2}}\)
Ejercicio 8
Considera el punto A(-1,1,3) y la recta r determinada por los puntos B(2,1,1) y C(0,1,-1)
Apartado a)
Halla la distancia del punto A a la recta r
En este ejercicio es más de lo mismo; definir un plano y empezar a calcular puntos en el espacio. Tenemos en este caso una recta y un punto. La distancia entre ambos elementos es equivalente al segmento perpendicular a la recta que pasa por dicho punto.
Para calcular dicho segmento, el procedimiento será:
- Calculo el plano perpendicular a la recta
- Posiciono el plano en el espacio tal que contenga a dicho punto A
- Obtengo el punto de la recta D que corta al plano
- La distancia es el módulo del segmento |AD|
Esta vez iré más rápido porque el ejercicio es idéntico al anterior.
El vector que define la recta sería el (-2, 0, -2), la ecuación del plano sería \(-x-z+E = 0\), y sustituyendo el punto A la ecuación final del plano sería:
\(-x-z + 2 = 0\)
De nuevo, parametrizamos la recta:
- x = 2 -m
- y = 1
- z = 1 -m
De forma que con m=0 estamos en el punto B y con m=2 estaríamos en el punto C. Sustituyendo en la ecuación del plano:
\( (-2+m) +(-1+m) +2 = 0 \rightarrow m = \dfrac{1}{2}\)
Por lo tanto, el punto que buscamos es el D = (1.5, 1, 0.5). La distancia que se pide es la longitud del segmento AD, es decir:
\(\boxed{|AD| = \sqrt{2.5^{2} + 2.5^{2}} = \dfrac{5}{\sqrt{2}} \ u}\)
Apartado b)
Calcula el área del triángulo cuyos vértices son A, B y C
Al igual que antes, el área de dicho triángulo sería base por altura dividido entre 2. La base sería la longitud del segmento BC, y la altura sería precisamente la longitud del segmento AD que justo acabamos de calcular.
La longitud de la base sería \(|BC| = \sqrt{4+4} = 2\sqrt{2} \ u\)
El área sería por lo tanto:
\(\boxed{\dfrac{2\sqrt{2} \cdot \dfrac{5}{\sqrt{2}} }{2} = 5 \ u^{2}}\)

![Examen Matemáticas Andalucía Junio 2024 Resuelto Selectividad [PEvAU] Examen_Titular-A_MATEMTICASII_compressed_page-0001](https://ingenieriabasica.es/wp-content/uploads/2024/06/Examen_Titular-A_MATEMTICASII_compressed_page-0001-142x200.jpg)